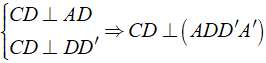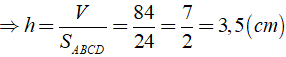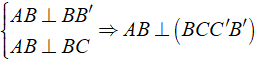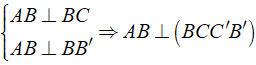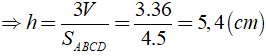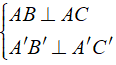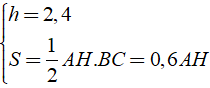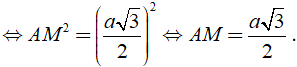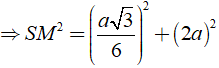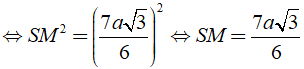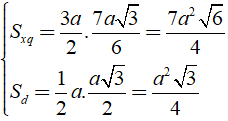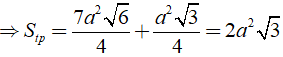Tổng hợp Lý thuyết & Trắc nghiệm Chương 4 Hình học 8 (có đáp án)
-
892 lượt thi
-
46 câu hỏi
-
100 phút
Danh sách câu hỏi
Câu 1:
Số mặt, số đỉnh, số cạnh của hình lập phương là?
 Xem đáp án
Xem đáp án
Hình lập phương cũng được gọi là hình hộp chữ nhật có 6 mặt, 8 đỉnh, 12 cạnh.
Chọn đáp án B.
Câu 2:
Hình hộp chữ nhật có số cặp mặt song song là?
 Xem đáp án
Xem đáp án
Hình hộp chữ nhật có 3 cặp mặt song song.
Chọn đáp án B.
Câu 4:
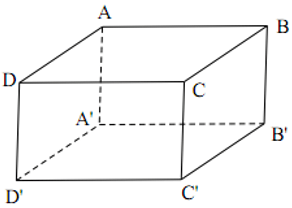
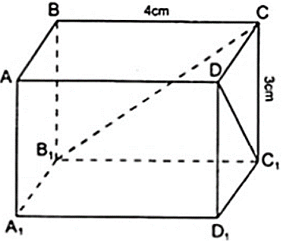
Cho hình hộp chữ nhật ABCD.A'B'C'D'. Chọn phát biểu đúng?
 Xem đáp án
Xem đáp án
Ta có: ABCD là mặt đáy hình chữ nhật
⇒ AB//CD
Chọn đáp án A.
Câu 5:
Trong các phát biểu sau, phát biểu nào sau đây sai?
 Xem đáp án
Xem đáp án
Tính chất của hai mặt phẳng song song là: Hai mặt phẳng song song với nhau thì không có điểm chung.
Vậy phát biểu D là phát biểu sai
Chọn đáp án D.
Câu 7:
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 2cm, AD = 3cm, AA' = 4cm. Thể tích hình hộp chữ nhật ABCD.A'B'C'D' ?
 Xem đáp án
Xem đáp án
Ta có:
Chọn đáp án B.
Câu 9:
Cho hình hộp chữ nhật ABCD.A'B'C'D' có diện tích đáy và có thể tích . Chiều cao của hình hộp chữ nhật có độ dài là?
 Xem đáp án
Xem đáp án
Ta có: Thể tích cua hình hộp chữ nhật là:
Vậy chiều cao của hình hộp chữ nhật là h = 3,5( cm )
Chọn đáp án B.
Câu 10:
Cho hình hộp chữ nhật ABCD.A'B'C'D'. Chọn phát biểu đúng trong các phát biểu sau:
 Xem đáp án
Xem đáp án
Ta có:
Mà AB ∈ ( ABB'A' ) ⇒ ( ABB'A' ) ⊥ ( BCC'B' )
Chọn đáp án C.
Câu 14:
Chọn phát biểu đúng trong các phát biểu sau:
 Xem đáp án
Xem đáp án
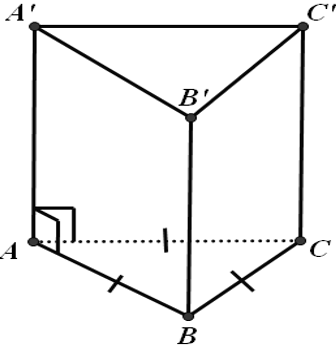
Hình lăng trụ tam giác gồm 5 mặt và 6 đỉnh.
+ 5 mặt:
( A'B'C' ), ( BCC'B' ), ( ABC ), ( A'C'CA ),( ABB'A' )
+ 6 đỉnh là: A,B,C,A',B',C'
Chọn đáp án B.
Câu 15:
Chọn phát biểu sai trong các phát biểu sau?
 Xem đáp án
Xem đáp án
Áp dụng định nghĩa của hình chóp: Hình chóp đều là hình chóp có đáy là một đa giác đều, các mặt bên là những tam giác cân bằng nhau có chung đỉnh.
Phát biểu A sai.
Chọn đáp án A.
Câu 16:
Mặt bên của hình chóp cụt đều là hình gì?
 Xem đáp án
Xem đáp án
Áp dụng định nghĩa của hình thang cân ta có: Mỗi mặt bên của hình chóp cụt đều là một hình thang cân.
Chọn đáp án C.
Câu 17:
Hình chóp tứ giác đều có mặt bên là hình gì?
 Xem đáp án
Xem đáp án
Hình chóp tứ giác đều có mặt bên là tam giác cân.
Chọn đáp án A.
Câu 18:
Hình chóp lục giác đều có bao nhiêu mặt?
 Xem đáp án
Xem đáp án
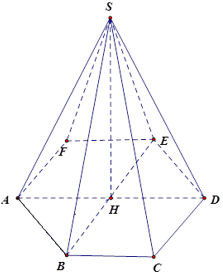
Hình chóp lục giác đều gồm có 6 mặt bên và 1 mặt đáy.
Chọn đáp án D.
Câu 19:
Các mặt bên của hình lăng trụ đứng là hình gì?
 Xem đáp án
Xem đáp án
Hình lăng trụ đứng là hình có 2 mặt đáy là các đa giác, các mặt bên là hình chữ nhật
Chọn đáp án C.
Câu 20:
Các mặt bên của hình lăng trụ đứng?
 Xem đáp án
Xem đáp án
Các mặt bên của hình lăng trụ đứng thì luôn song song với nhau, vuông góc với 2 mặt đáy và bằng nhau.
Chọn đáp án D.
Câu 21:
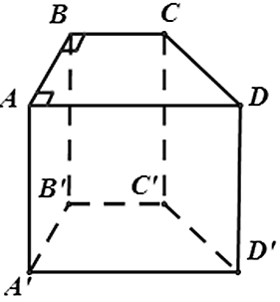
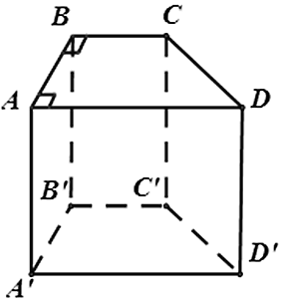
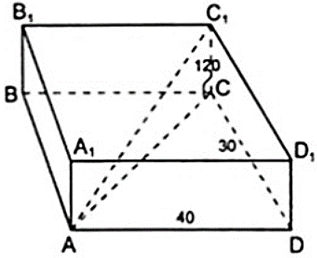
Cho hình lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là hình thang vuông . Có bao nhiêu cạnh song song với mặt phẳng ( BCC'B' )
 Xem đáp án
Xem đáp án
Vì
nên các đường thẳng AA',DD',AD,A'D' song song với mặt phẳng ( BCC'B' ).
Chọn đáp án B.
Câu 22:
Cho hình lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là hình thang vuông . Có bao nhiêu cạnh vuông góc với mặt phẳng ( BCC'B' ) ?
 Xem đáp án
Xem đáp án
Vì
Tương tự: A'B' ⊥ ( BCC'B' ) ⇒ AB,A'B' ⊥ ( BCC'B' )
Chọn đáp án A.
Câu 24:
Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD có AB = 4cm,BC = 5cm. Biết thể tích của hình chóp S.ABCD bằng . Tính độ dài đường cao của hình chóp?
 Xem đáp án
Xem đáp án
Áp dụng công thức thể tích của hình chóp ta có:
Chọn đáp án C.
Câu 26:
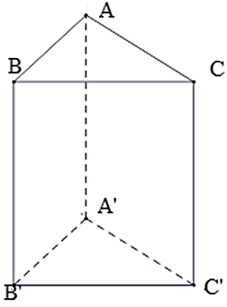
Cho hình lăng trụ đứng ABC.A'B'C' có AB = 5cm, AC = 12cm,BC = 13cm. Có bao nhiêu mặt phẳng vuông góc với mặt phẳng ( ABB'A' ) ?
 Xem đáp án
Xem đáp án
Ta có: ⇒ Δ ABC vuông tại A.
Do đó:
Vì AC vuông góc với hai đường thẳng cắt nhau là AB và AA'
Nên AC ⊥ ( ABB'A' )
Vậy có 3 mặt phẳng vuông góc với ( ABB'A' ) là:
( ABC ), ( A'B'C' ),( ACC'A' )
Chọn đáp án D.
Câu 27:
Cho hình lăng trụ đứng ABC.A'B'C' có ,AB = 6cm, AC = 8cm, AA' = 15cm. Diện tích toàn phần của hình lăng trụ đó?
 Xem đáp án
Xem đáp án
Ta có tam giác ABC vuông tại A
Câu 28:
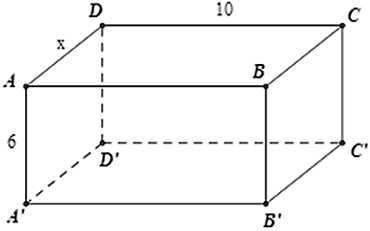
Cho hình hộp chữ nhật có diện tích xung quanh bằng tổng diện tích hai đáy, chiều cao bằng 6cm. Một kích thức của đáy bằng 10cm. tính kích thước còn lại?
 Xem đáp án
Xem đáp án
Chu vi của đáy bằng: 2( x + 10 )
Diện tích xung quanh: Sxq = 2( x + 10 ).6 = 12( x + 10 )
Diện tích đáy: 10x
Theo giả thiết ta có: 12( x + 10 ) = 20x ⇔ x = 15
Chọn đáp án A.
Câu 29:
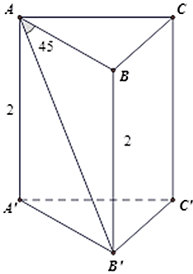
Cho hình lăng trụ tam giác đều ABC.A'B'C' có chiều cao bằng 2cm, . Tính diện tích xung quanh của hình lăng trụ?
 Xem đáp án
Xem đáp án
Tam giác vuông ABB' có nên là tam giác vuông cân tại B nên AB = BB' = 2cm.
Vì ABC là tam giác đều nên chu vi đáy bằng 6( cm )
Khi đó diện tích xung quanh hình lăng trụ là
Chọn đáp án C.
Câu 31:
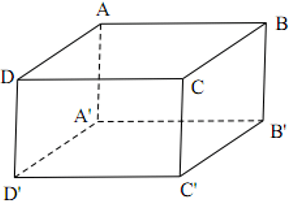
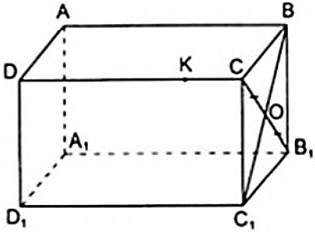
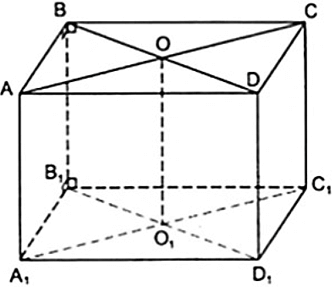
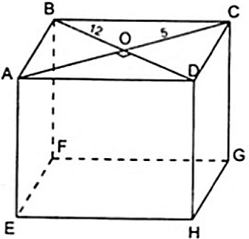
Cho hình hộp chữ nhật ABCD.A'B'C'D'. Nếu O là trung điểm của đoạn thì O có là điểm thuộc đoạn ?
 Xem đáp án
Xem đáp án
Câu trả lời trên là có. Thật vậy, vì mặt bên là hình chữ nhật có O là trung điểm của đường chéo nên O cũng là trung điểm của đường chéo (theo tính chất đường chéo của hình chữ nhật). Vậy thuộc đoạn
Câu 32:
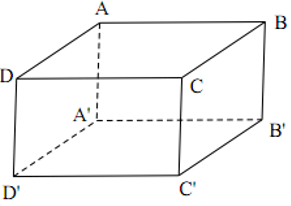
Cho hình hộp chữ nhật ABCD.A'B'C'D'. K là điểm thuộc cạnh CD, liệu K có thể là điểm thuộc cạnh hay không?
 Xem đáp án
Xem đáp án
K không thuộc cạnh vì mà thuộc mặt phẳng đó
Vậy K không thuộc cạnh
Câu 34:
Xét sự đúng sai trong các phát biểu sau? Hình chóp đều có đáy là hình thoi và chân đường cao trùng với giao điểm hai đường chéo của đáy.
 Xem đáp án
Xem đáp án
Sai, vì hình thoi không phải là tứ giác đều (các góc không bằng nhau).
Câu 35:
Xét sự đúng sai trong các phát biểu sau? Hình chóp đều có đáy là hình chữ nhật và chân đường cao trùng với giao điểm hai đường chéo của đáy.
 Xem đáp án
Xem đáp án
Sai, vì hình chữ nhật không phải là tứ giác đều (các cạnh không bằng nhau).
Câu 41:
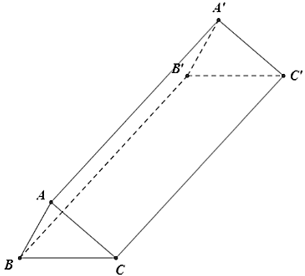
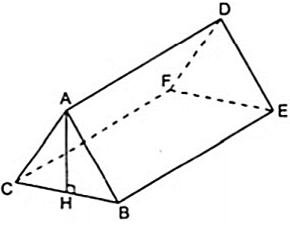
Một trại hè có dạng hình lăng trụ đứng đáy tam giác, thể tích hình không gian bên trong là . Biết chiều dài lều AD = 2,4( cm ), chiều rộng của lều là 1,2cm. Tính chiều cao AH của lều?
 Xem đáp án
Xem đáp án
Áp dụng công thức thể tích của hình lăng trụ đứng ta có: V = S.h
Ta có:
Do đó: V = S.h = 0,6AH.2,4 = 1,44AH
Theo giả thiết ta có: 1,44AH = 2,16 ⇔ AH = 1,5( cm )
Câu 44:
Tính diện tích toàn phần của hình chóp tam giác đều có cạnh đáy bằng a và chiều cao bằng 2a.
 Xem đáp án
Xem đáp án
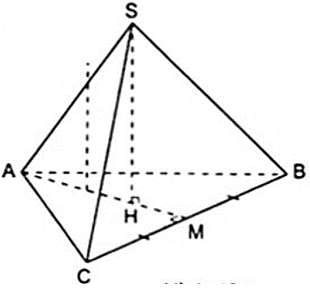
Xét hình chóp S.ABC có AB = AC = BC = a và SH = 2a.
Gọi M là trung điểm của BC thì AM vừa là đường trung tuyến, vừa là đường cao, vừa là đường phân giác của tam giác đều ABC nên AM ⊥ BC và HM = 1/3AM.
Áp dụng định lý Py – ta – go vào tam giác vuông ABM vuông tại M ta được:
Do đó HM = (a√3 )/6.
Áp dụng định lí Py – ta – go vào tam giác vuông SHM vuông tại H, ta có:
Áp dụng công thức:
Ta có: