Giải SGK Toán 8 Cánh diều Bài 17. Hình bình hành có đáp án
-
108 lượt thi
-
17 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Trong thiết kế tay vịn cầu thang (Hình 34), người ta thường để các cặp thanh sườn song song với nhau, các cặp thanh trụ song song với nhau, tạo nên các hình bình hành.
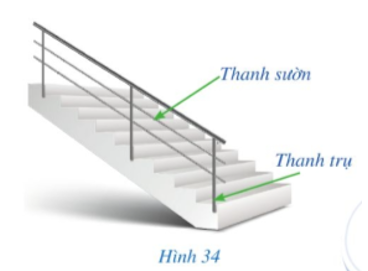
Hình bình hành có những tính chất gì? Có những dấu hiệu nào để nhận biết một tứ giác là hình bình hành?
Xem đáp án
Sau bài học này, chúng ta sẽ giải quyết được câu hỏi trên như sau:
‒ Hình bình hành có:
+ Các cạnh đối song song và bằng nhau;
+ Các góc đối bằng nhau;
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
‒ Dấu hiệu nhận biết hình bình hành:
+ Tứ giác có các cặp cạnh đối song song với nhau là hình bình hành.
+ Tứ giác có các cặp cạnh đối bằng nhau là hình bình hành.
+ Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.
+ Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
+ Tứ giác có các cặp góc đối bằng nhau là hình bình hành.
Câu 2:
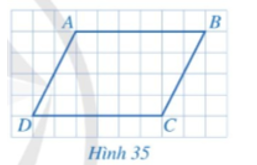
Cho biết các cặp cạnh đối AB và CD, AD và BC của tứ giác ABCD ở Hình 35 có song song với nhau hay không.
Xem đáp án
Tứ giác ABCD ở Hình 35 có các cặp cạnh đối AB // CD, AD // BC.
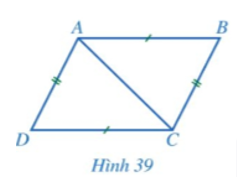
Câu 4:
b) So sánh các cặp góc: và ; và .
Xem đáp án
b) Do ΔABD = ΔCDB (câu a) nên (cặp góc tương ứng)
Chứng minh tương tự câu a ta cũng có ΔABC = ΔCDA (g.c.g)
Suy ra (cặp góc tương ứng).
Câu 5:
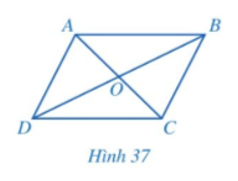
c) Hai tam giác OAB và OCD có bằng nhau hay không? Từ đó, hãy so sánh các cặp đoạn thẳng: OA và OC; OB và OD.
Xem đáp án
c) Xét ΔOAB và ΔOCD có:
(do AB // CD);
AB = CD (theo câu a);
(do AB // CD).
Do đó ΔOAB = ΔOCD (g.c.g)
Suy ra OA = OC và OB = OD (các cặp cạnh tương ứng).
Câu 9:
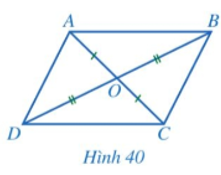
Cho tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại O thoả mãn OA = OC và . Chứng minh tứ giác ABCD là hình bình hành.
Xem đáp án
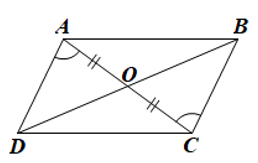
• Xét ΔOAD và ΔOCB có:
(giả thiết);
OA = OC (giả thiết);
(đối đỉnh)
Do đó ΔOAD = ΔOCB (g.c.g)
Suy ra OD = OB (hai cạnh tương ứng)
• Xét tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại trung điểm O của mỗi đường
Do đó ABCD là hình bình hành.
Câu 12:
c) Tứ giác ABCD là hình bình hành.
Xem đáp án
c) Xét tứ giác ABCD có: , (giả thiết)
Do đó tứ giác ABCD là hình bình hành (dấu hiệu nhận biết).
Câu 14:
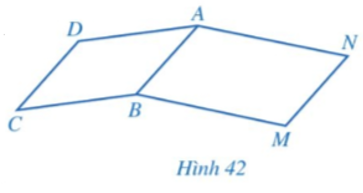
Cho hai hình bình hành ABCD và ABMN (Hình 42). Chứng minh:
a) CD = MN;
Xem đáp án
a) Vì ABCD là hình bình hành (giả thiết) nên AB = CD (tính chất) (1)
Vì ABMN là hình bình hành (giả thiết) nên AB = MN (tính chất) (2)
Từ (1), (2) suy ra CD = MN.
Câu 16:
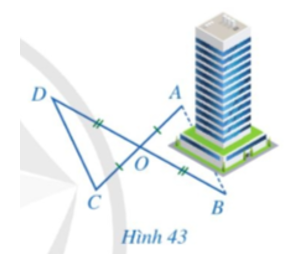
Để đo khoảng cách giữa hai vị trí A, B ở hai phía của một toà nhà mà không thể trực tiếp đo được, người ta làm như sau: Chọn các vị trí O, C, D sao cho O không thuộc đường thẳng AB; khoảng cách CD là đo được; O là trung điểm của cả AC và BD (Hình 43). Người ta đo được CD = 100 m. Tính độ dài của AB.
Xem đáp án
Xét tứ giác ABCD có: hai đường chéo AC và BD cắt nhau tại trung điểm O của mỗi đường nên là hình bình hành.
Do đó AB = CD = 100 (m).
Câu 17:
Bạn Hoa vẽ tam giác ABC lên tờ giấy sau đó cắt một phần tam giác ở phía góc C (Hình 44). Bạn Hoa đố bạn Hùng: Không vẽ lại tam giác ABC, làm thế nào tính được độ dài các đoạn thẳng AC, BC và số đo góc ACB?
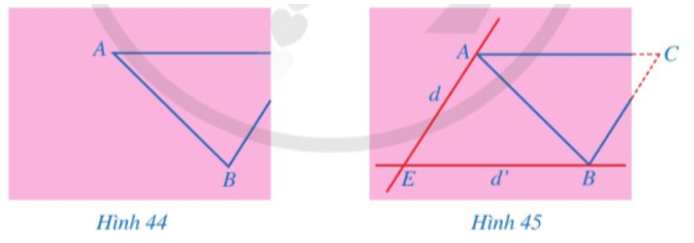
Bạn Hùng đã làm như sau:
– Qua điểm A kẻ đường thẳng d song song với BC, qua điểm B kẻ đường thẳng d’ song song với AC;
– Gọi E là giao điểm của d và d’;
– Đo độ dài các đoạn thẳng AE, BE và đo góc AEB. Từ đó, tính được độ dài các đoạn thẳng AC, BC và số đo góc ACB (Hình 45).
Em hãy giải thích cách làm của bạn Hùng.
Xem đáp án
• Vì d // BC (giả thiết) nên AE // BC;
Vì d’ // AC (giả thiết) nên BE // AC.
• Xét tứ giác ACBE có: AE // BC (chứng minh trên) và BE // AC (chứng minh trên)
Do đó tứ giác ACBE là hình bình hành
Suy ra (tính chất hình bình hành)
Bạn Hùng chứng minh được tứ giác ACBE là hình bình hành có các tính chất trên, đo độ dài các đoạn thẳng BE, AE và đo góc AEB. Từ đó, tính được độ dài các đoạn thẳng AC, BC và số đo góc ACB (Hình 45).