Giải SGK Toán 8 HĐTN Thực hiện tính toán trên đa thức với phần mềm GeoGebra có đáp án
Giải SGK Toán 8 HĐTN Thực hiện tính toán trên đa thức với phần mềm GeoGebra có đáp án
-
147 lượt thi
-
7 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Tính:.
 Xem đáp án
Xem đáp án
Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới
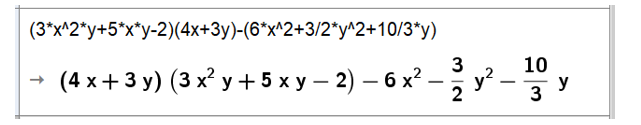
Câu 2:
Khai triển các biểu thức sau:
a) (5x – y)2;
 Xem đáp án
Xem đáp án
a) Khai triển biểu thức (5x – y)2:
• Sử dụng lệnh Expand(<biểu thức cần khai triển>).
• Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới.

Vậy (5x – y)2 = 25x2 – 10xy + y2.
Câu 3:
 Xem đáp án
Xem đáp án
b) Khai triển biểu thức :
• Sử dụng lệnh Expand(<biểu thức cần khai triển>).
• Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới.
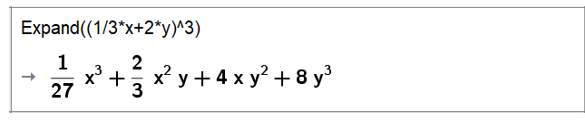
Vậy .
Câu 4:
Phân tích các đa thức sau thành nhân tử:
a) x4 – 4x3 – 7x2 + 8x + 10;
 Xem đáp án
Xem đáp án
`a) Phân tích các đa thức x4 – 4x3 – 7x2 + 8x + 10 thành nhân tử:
• Sử dụng lệnh Factor(<đa thức>) (hoặc Factorise(<đa thức>)).
• Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới.
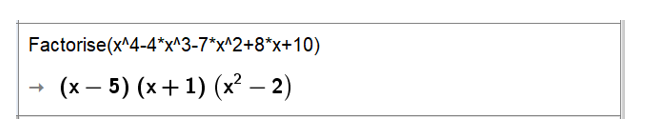
Vậy x4 – 4x3 – 7x2 + 8x + 10 = (x – 5)(x + 1)(x2 – 2).
Câu 5:
Phân tích các đa thức sau thành nhân tử:
b) (x + y + z)3 – x3 – y3 – z3.
 Xem đáp án
Xem đáp án
b) Phân tích các đa thức (x + y + z)3 – x3 – y3 – z3 thành nhân tử:
• Sử dụng lệnh Factor(<đa thức>) (hoặc Factorise(<đa thức>)).
• Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới

Vậy (x + y + z)3 – x3 – y3 – z3 = 3(y + z)(x + z)(x + y).
Câu 6:
Tìm thương và dư (nếu có) trong các phép chia sau:
a) (3x4y – 9x3y2 – 21x2y2) : (3x2y);
 Xem đáp án
Xem đáp án
a) Tìm thương và dư (nếu có) trong các phép chia (3x4y – 9x3y2 – 21x2y2) : (3x2y).
• Sử dụng lệnh Division(<đa thức bị chia>, <đa thức chia>) để tìm thương và dư của phép chia hai đa thức.
• Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới

Vậy phép chia hai đa thức (3x4y – 9x3y2 – 21x2y2) cho (3x2y), ta được thương là x2 – 3xy – 7y và dư 0.
Câu 7:
b) (2x3 + 5x2 – 2x + 12) : (2x2 – x + 1).
 Xem đáp án
Xem đáp án
b) Tìm thương và dư (nếu có) trong các phép chia (2x3 + 5x2 – 2x + 12) : (2x2 – x + 1).
• Sử dụng lệnh Division(<đa thức bị chia>, <đa thức chia>) để tìm thương và dư của phép chia hai đa thức.
• Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới
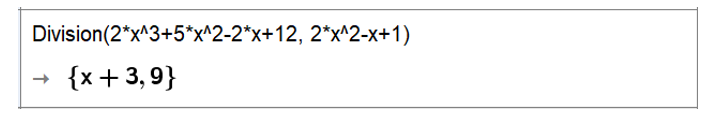
Vậy phép chia hai đa thức (2x3 + 5x2 – 2x + 12) cho (2x2 – x + 1), ta được thương là x + 3 và dư 9.
