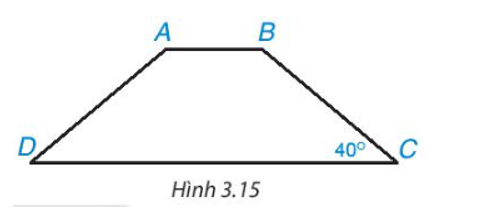
Giải SGK Toán 8 KNTT Bài 11. Hình thang cân có đáp án
-
246 lượt thi
-
16 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
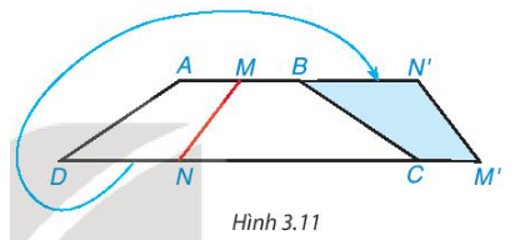
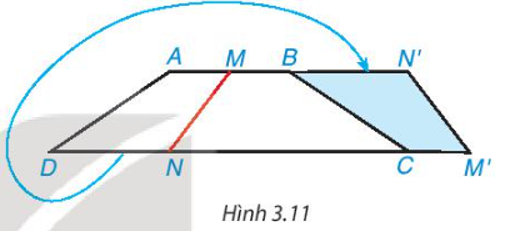
Cắt một mảnh giấy hình thang cân bằng một nhát thẳng cắt cả hai cạnh đáy thì được hai hình thang. Lật một trong hai hình thang đó rồi ghép với hình thang còn lại dọc theo các cạnh bên của hình thang ban đầu (Hình 3.11). Hãy giải thích tại sao hình tạo thành cũng là một hình thang cân.
 Xem đáp án
Xem đáp án
Sau bài học này ta giải quyết được bài toán như sau:
Ta cắt một mảnh giấy hình thang cân bằng một nhát thẳng cắt cả hai cạnh đáy.
Lật một trong hai hình thang đó rồi ghép với hình thang còn lại dọc theo các cạnh bên của hình thang ban đầu nên .
Tứ giác ABCD là hình thang cân nên AB // CD suy ra MN’ // M’N.
Do đó MN’M’N là hình thang.
Hình thang MN’M’N có nên MN’M’N là hình thang cân.
Câu 3:
Cho hình thang cân ABCD, AC // CD và AB < CD (H.3.16).
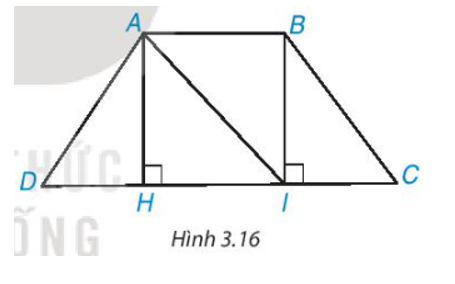
a) Từ A và B kẻ AH ⊥ DC, BI ⊥ DC, H ∈ CD, I ∈ CD. Chứng minh rằng AH = BI bằng cách chứng minh ∆AHI = ∆IBA.
 Xem đáp án
Xem đáp án
a) Vì ABCD là hình thang cân (AC // CD) nên (hai góc so le trong).
Ta có AH ⊥ DC, BI ⊥ DC suy ra AH // BI.
Do đó (hai góc so le trong).
Xét ∆AHI và ∆IBA có:
(chứng minh trên);
Cạnh AI chung;
(hai góc so le trong).
Do đó ∆AHI = ∆IBA (c.g.c).
Suy ra AH = BI (hai cạnh tương ứng).
Câu 4:
b) Chứng minh ∆AHD = ∆BIC, từ đó suy ra AD = BC.
 Xem đáp án
Xem đáp án
b) Vì ABCD là hình thang cân (AC // CD) nên AD = BC; .
Xét ∆AHD và ∆BIC có:
(vì AH ⊥ DC, BI ⊥ DC, H ∈ CD, I ∈ CD);
AD = BC (chứng minh trên);
(chứng minh trên).
Do đó ∆AHD = ∆BIC (cạnh huyền – góc nhọn).
Suy ra AD = BC (hai cạnh tương ứng).
Câu 5:
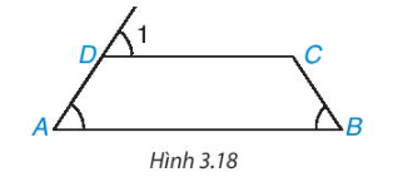
Cho tứ giác ABCD như Hình 3.18. Biết rằng . Chứng minh rằng AB = BC.
 Xem đáp án
Xem đáp án
Ta có mà hai góc này ở vị trí đồng vị nên AB // CD.
Suy ra tứ giác ABCD là hình thang.
Mặt khác hình thang ABCD có nên ABCD là hình thang cân.
Do đó AB = BC (đpcm).
Câu 6:
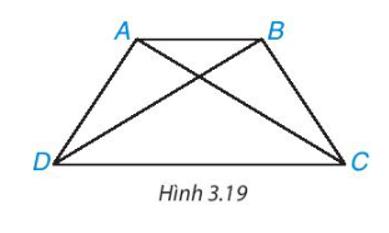
Cho hình thang cân ABCD, kẻ hai đường chéo AC, BD (H.3.19). Hãy chứng minh ∆ACD = ∆BDC. Từ đó suy ra AC = BD
 Xem đáp án
Xem đáp án
Vì ABCD là hình thang cân (AC // CD) nên AD = BC; .
Xét ∆ACD và ∆BDC có
AD = BC (chứng minh trên);
(chứng minh trên);
Cạnh CD chung.
Do đó ∆ACD = ∆BDC (c.g.c).
Suy ra AC = BD (hai góc tương ứng).
Câu 7:
Cho tam giác ABC cân tại A. Kẻ một đường thẳng d song song với BC, d cắt cạnh AB tại D và cắt cạnh AC tại E (H.3.20).
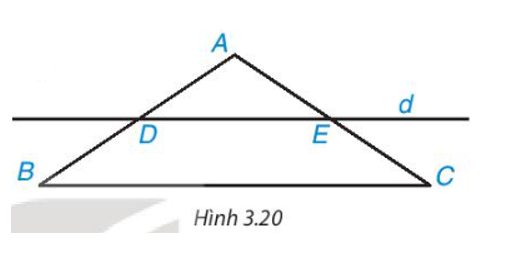
a) Tứ giác DECB là hình gì?
 Xem đáp án
Xem đáp án
a) Theo đề bài: d // BC nên DE // BC
Suy ra DECB là hình thang.
Vì tam giác ABC cân tại A nên .
Hình thang DECB có nên tứ giác DECB là hình thang cân.
Câu 8:
b) Chứng minh BE = CD.
 Xem đáp án
Xem đáp án
b) Hình thang cân DECB có BE và CD là hai đường chéo.
Do đó BE = CD (đpcm).
Câu 9:
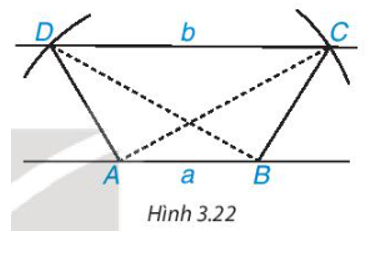
a) Vẽ hình thang có hai đường chéo bằng nhau theo các bước sau:
- Vẽ hai đường thẳng song song a, b. Trên a lấy hai điểm A, B.
- Vẽ hai cung tròn tâm A và B có cùng bán kính sao cho cung tròn tâm A cắt b tại C; cung tròn tâm B cắt b tại D và hai đoạn thẳng AC, BD cắt nhau. Hình thang ABCD có hai đường chéo AC và BD bằng nhau.
 Xem đáp án
Xem đáp án
a) Học sinh vẽ hình theo các bước đã nêu ở đề bài.
Câu 10:
 Xem đáp án
Xem đáp án
b) Hình thang ABCD có hai đường chéo AC = BD.
Do đó ABCD là hình thang cân.
Câu 11:
Cắt một mảnh giấy hình thang cân bằng một nhát thẳng cắt cả hai cạnh đáy thì được hai hình thang. Lật một trong hai hình thang đó rồi ghép với hình thang còn lại dọc theo các cạnh bên của hình thang ban đầu (Hình 3.11). Hãy giải thích tại sao hình tạo thành cũng là một hình thang cân.
 Xem đáp án
Xem đáp án
Ta cắt một mảnh giấy hình thang cân bằng một nhát thẳng cắt cả hai cạnh đáy.
Lật một trong hai hình thang đó rồi ghép với hình thang còn lại dọc theo các cạnh bên của hình thang ban đầu nên .
Tứ giác ABCD là hình thang cân nên AB // CD suy ra MN’ // M’N.
Do đó MN’M’N là hình thang.
Hình thang MN’M’N có nên MN’M’N là hình thang cân.
Câu 12:
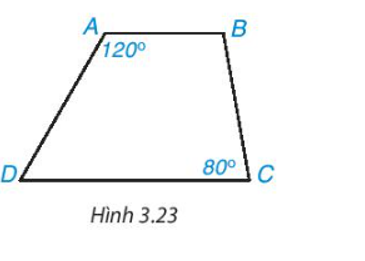
Hình thang trong Hình 3.23 có là hình thang cân không? Vì sao
 Xem đáp án
Xem đáp án
Để hình thang ABCD là hình thang cân thì .
Suy ra (không thỏa mãn định lí tổng bốn góc trong một tứ giác).
Khi đó, ACBD không phải là tứ giác.
Do đó ACBD cũng không phải là hình thang cân.
Câu 13:
Cho hình thang ABCD (AB // CD). Kẻ đường thẳng vuông góc với AC tại C và đường thẳng vuông góc với BD tại D, hai đường thẳng này cắt nhau tại E. Chứng minh rằng nếu EC = ED thì hình thang ABCD là hình thang cân.
 Xem đáp án
Xem đáp án
Gọi O là giao điểm của AC và BD.
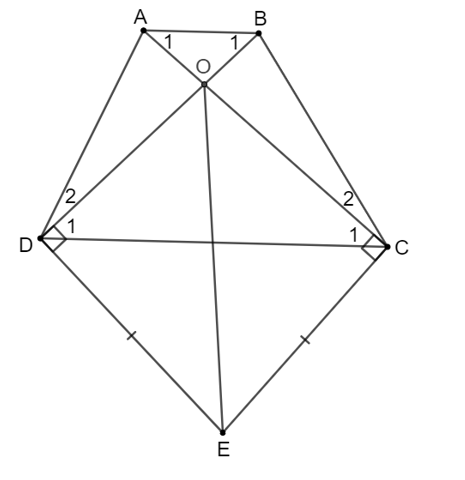
Xét ∆DOE và ∆COE có:
(vì OD ⊥ DE; OC ⊥ CE)
EC = ED (giả thiết)
Cạnh OE chung
Do đó ∆DOE = ∆COE (cạnh huyền – cạnh góc vuông).
Suy ra OC = OD (hai cạnh tương ứng).
Do đó tam giác OCD cân tại O nên .
Vì ABCD là hình thang nên AB // CD suy ra (cặp góc so le trong).
Do đó (vì ).
Suy ra tam giác OAB cân tại O nên OA = OB.
Xét ∆OAD và ∆OBC có:
OA = OB (chứng minh trên)
(hai góc đối đỉnh)
OC = OD (chứng minh trên)
Do đó ∆OAD = ∆OBC (c.g.c)
Suy ra (hai góc tương ứng).
Ta có .
Mà nên .
Hình thang ABCD có nên ABCD là hình thang cân.
Câu 14:
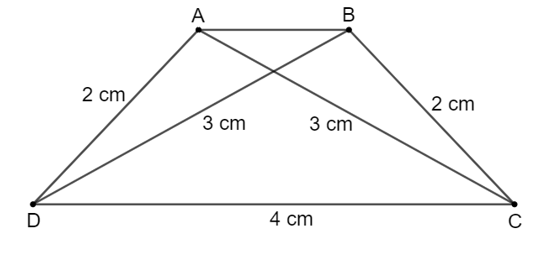
Vẽ hình thang cân ABCD (AB // CD) biết đáy lớn CD dài 4 cm, cạnh bên dài 2 cm và đường chéo dài 3 cm.
 Xem đáp án
Xem đáp án
Cách vẽ hình thang cân ABCD có đáy lớn CD dài 4 cm, cạnh bên dài 2 cm và đường chéo dài 3 cm:
- Vẽ cạnh CD = 4 cm.
- Dùng compa vẽ hai đường tròn (D; 2 cm) và (C; 3 cm). Hai đường tròn này cắt nhau tại điểm A.
- Dùng compa vẽ hai đường tròn (C; 3 cm) và (D; 2 cm). Hai đường tròn này cắt nhau tại điểm B.
- Nối AB, AD, BC ta được hình thang ABCD (như hình vẽ).
Câu 15:
Hai tia phân giác của hai góc A, B của hình thang cân ABCD (AB // CD) cắt nhau tại điểm E trên cạnh đáy CD. Chứng minh rằng EC = ED.
 Xem đáp án
Xem đáp án
Vì ABCD là hình thang cân nên .
Theo đề bài, ta có AE, BE lần lượt là tia phân giác của và .
Suy ra .
Mà nên .
Xét tam giác EAB cân tại E (vì ) nên EA = EB.
Xét ∆ADE và ∆BCE có:
EA = EB (chứng minh trên)
(chứng minh trên)
AD = BC (chứng minh trên)
Do đó ∆ADE = ∆BCE (c.g.c).
Suy ra EC = ED (hai cạnh tương ứng).
Câu 16:
Hình thang cân ABCD (AB // CD, AB < CD) có các đường thẳng AD, BC cắt nhau tại I, các đường thẳng AC, BD cắt nhau tại J. Chứng minh rằng đường thẳng IJ là đường trung trực của đoạn thẳng AB.
 Xem đáp án
Xem đáp án
Gọi O là giao điểm của AB và IJ.
Vì ABCD là hình thang cân nên .
Xét ∆ABD và ∆BAC có:
AC = BD (chứng minh trên);
(chứng minh trên);
AD = BC (chứng minh trên).
Do đó ∆ABD = ∆BAC (c.g.c)
Suy ra (hai góc tương ứng).
Tam giác ICD cân tại I (vì ) nên IC = ID.
Vì nên .
Tam giác JCD cân tại J (vì ) nên JC = JD.
Xét ∆IJD và ∆IJC có:
IC = ID (chứng minh trên);
(chứng minh trên);
JC = JD (chứng minh trên).
Do đó ∆IJD = ∆IJC (c.g.c).
Suy ra (hai góc tương ứng).
Ta có ID = IC, AD = BC.
Mà ID = AI + AD; IC = IB + BC nên IA = IB.
Tam giác IAB cân tại I (vì IA = IB) có IO là tia phân giác
Suy ra IO là đường trung trực của đoạn thẳng AB.
Vậy đường thẳng IJ là đường trung trực của đoạn thẳng AB.