Giải SGK Toán 8 KNTT Bài 13. Hình chữ nhật có đáp án
-
123 lượt thi
-
12 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
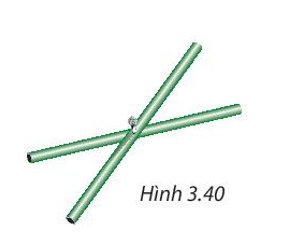
Hai thanh tre thẳng bằng nhau, được gắn với nhau tại trung điểm của mỗi thanh. Khi các đầu mút của hai thanh tre đó tạo thành bốn đỉnh của một tứ giác (H.3.40) thì tứ giác đó là hình gì? Tại sao?
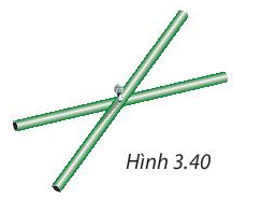
 Xem đáp án
Xem đáp án
Sau bài học này ta giải quyết được bài toán như sau:
Hai đầu mút của hai thanh tre tạo thành bốn đỉnh của tứ giác.
Tứ giác đó có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường nên tứ giác đó là hình chữ nhật.
Vậy khi các đầu mút của hai thanh tre đó tạo thành bốn đỉnh của một tứ giác thì tứ giác đó là hình chữ nhật.
Câu 2:
Trong các hình dưới đây, hình nào là hình chữ nhật? Tại sao?
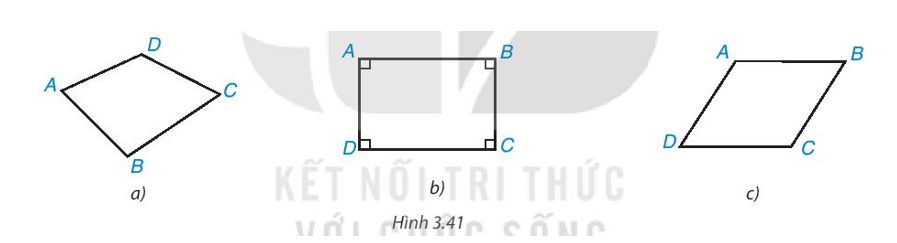
 Xem đáp án
Xem đáp án
Tứ giác ABCD trong Hình 3.41b là hình chữ nhật vì có .
Tứ giác ABCD trong Hình 3.41a và Hình 3.41c không phải là hình chữ nhật vì không có 4 góc vuông.
Câu 3:
Hình chữ nhật có là hình bình hành không, có là hình thang cân không? Tại sao?
Ta có tính chất sau đây về đường chéo của hình chữ nhật.
 Xem đáp án
Xem đáp án
Ta đặt hình chữ nhật ABCD như hình vẽ.
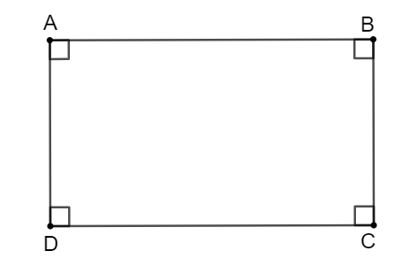
Vì ABCD là hình chữ nhật .
Ta có: AB ⊥ AD; AB ⊥ BC suy ra AD // BC.
AB ⊥ AD; CD ⊥ AD suy ra AB // CD.
• Vì ABCD là hình chữ nhật nên AD // BC; AB // CD
Suy ra ABCD cũng là hình bình hành.
• Vì ABCD là hình chữ nhật nên AB // CD suy ra ABCD cũng là hình thang.
Hình thang ABCD có .
Do đó ABCD cũng là hình thang cân.
Vì ABCD vừa là hình bình hành vừa là hình thang cân nên có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.
Câu 4:
Cho hình chữ nhật ABCD. Hai đường chéo AC, BD cắt nhau tại O. Kẻ OH ⊥ DC (H.3.44). Chứng minh rằng H là trung điểm của DC.
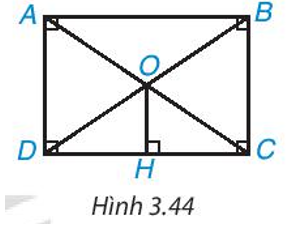
 Xem đáp án
Xem đáp án
Vì ABCD là hình chữ nhật có hai đường chéo AC và BD bằng nhau và cắt nhau tại trung điểm của mỗi đường.
Suy ra OA = OB = OC = OD.
Xét tam giác OCD cân tại O (vì OC = OD) có OH là đường cao nên OH cũng là đường trung tuyến.
Do đó CH = DH.
Vậy H là trung điểm của DC.
Câu 5:
Cho hình bình hành ABCD có góc A vuông. Tính các góc B, C, D. Tứ giác ABCD có là hình chữ nhật không? Vì sao?
 Xem đáp án
Xem đáp án
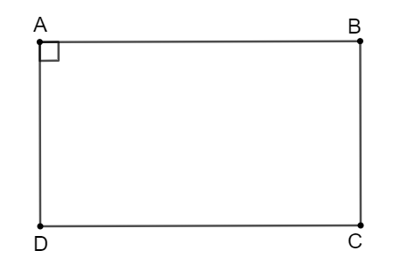
Vì ABCD là hình bình hành nên
Suy ra
Ta có
Do đó .
Tứ giác ABCD là hình bình hành vì .
Câu 6:
Cho tứ giác ABCD có hai đường chéo cắt nhau tại trung điểm O của mỗi đường. Hỏi tứ giác ABCD là hình gì? Tại sao?
 Xem đáp án
Xem đáp án
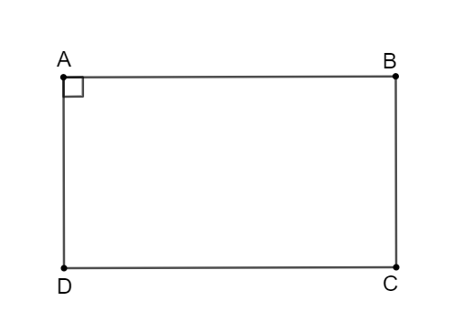
Tứ giác ABCD có hai đường chéo cắt nhau tại trung điểm O của mỗi đường nên tứ giác ABCD là hình bình hành.
Hình bình hành ABCD là có
Do đó, tứ giác ABCD là hình chữ nhật.
Câu 7:
Hãy trả lời các câu hỏi trong tình huống mở đầu.
Hai thanh tre thẳng bằng nhau, được gắn với nhau tại trung điểm của mỗi thanh. Khi các đầu mút của hai thanh tre đó tạo thành bốn đỉnh của một tứ giác (H.3.40) thì tứ giác đó là hình gì? Tại sao
 Xem đáp án
Xem đáp án
Hai đầu mút của hai thanh tre tạo thành bốn đỉnh của tứ giác.
Tứ giác đó có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường nên tứ giác đó là hình chữ nhật.
Vậy khi các đầu mút của hai thanh tre đó tạo thành bốn đỉnh của một tứ giác thì tứ giác đó là hình chữ nhật.
Câu 8:
Bằng ê ke, nêu cách kiểm tra một tứ giác có là hình chữ nhật hay không. Hãy giải thích kết quả.
 Xem đáp án
Xem đáp án
Dùng ê ke kiểm tra bốn góc của tứ giác đó:
• Nếu bốn góc của tứ giác đều là góc vuông thì tứ giác đó là hình chữ nhật;
• Nếu bốn góc của tứ giác có ít nhất một góc không vuông thì tứ giác đó không là hình chữ nhật.
Giải thích: Hình chữ nhật là tứ giác có bốn góc vuông.
Câu 9:
Bằng compa, nêu cách kiểm tra một tứ giác có là hình chữ nhật hay không. Hãy giải thích kết quả.
 Xem đáp án
Xem đáp án
Ta kiểm tra xem các cặp đối của tứ giác:
• Nếu các cặp cạnh đối không bằng nhau thì tứ giác đó không là hình bình hành nên cũng không là hình chữ nhật.
• Nếu các cặp cạnh đối bằng nhau thì tứ giác đó là hình bình hành.
Sau đó ta kiểm tra xem hai đường chéo của tứ giác (là hình bình hành) đó.
• Nếu hai đường chéo của hình bình hành đó bằng nhau thì tứ giác đó là hình chữ nhật.
• Nếu hai đường chéo của hình bình hành đó không bằng nhau thì tứ giác đó không là hình chữ nhật.
Câu 10:
Cho tam giác ABC, đường cao AH. Gọi M là trung điểm của AC, N là điểm sao cho M là trung điểm của HN. Chứng minh tứ giác AHCN là hình chữ nhật.
 Xem đáp án
Xem đáp án
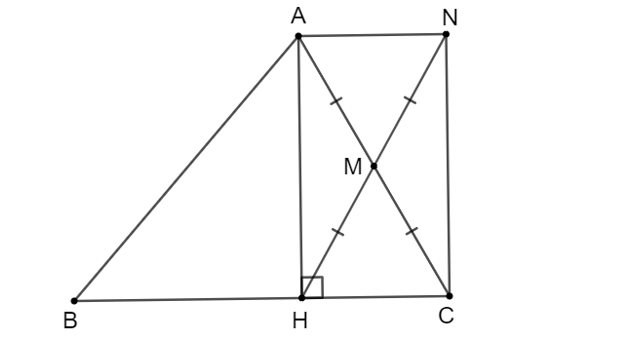
Theo đề bài, M là trung điểm của AC, N là điểm sao cho M là trung điểm của HN.
Nên tứ giác ANCH có hai đường chéo AC và HN cắt nhau tại trung điểm M của mỗi đường.
Suy ra tứ giác ANCH là hình bình hành.
Hình bình hành ANCH có nên tứ giác ANCH là hình chữ nhật.
Câu 11:
Xét một điểm M trên cạnh huyền của tam giác ABC vuông cân tại A. Gọi N và P lần lượt là hình chiếu vuông góc của M trên các cạnh AB và AC.
a) Hỏi tứ giác MPAN là hình gì?
 Xem đáp án
Xem đáp án
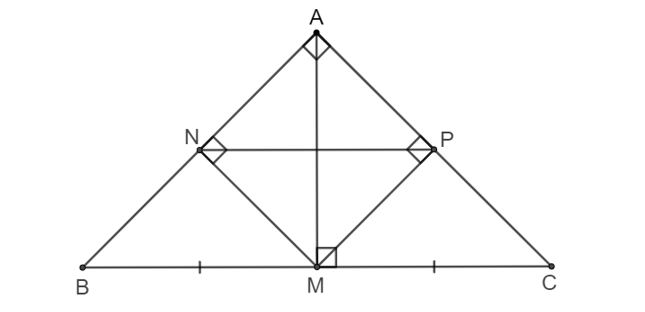
a) Tứ giác MPAN có:
Suy ra .
Tứ giác MPAN có: .
Do đó tứ giác MPAN là hình chữ nhật.
Câu 12:
b) Hỏi M ở vị trí nào thì đoạn thẳng NP có độ dài ngắn nhất? Vì sao?
 Xem đáp án
Xem đáp án
b) Vì tứ giác MPAN là hình chữ nhật có hai đường chéo AM và NP nên AM = NP.
Để đoạn thẳng NP có độ dài ngắn nhất thì AM có độ dài ngắn nhất.
Khi đó, MH là đường vuông góc kẻ từ A đến đoạn thẳng BC hay AM là đường cao của tam giác ABC.
Mà tam giác ABC vuông cân tại A nên AM cũng là đường trung tuyến.
Do đó M là trung điểm của BC.
Vậy M là trung điểm của đoạn thẳng BC thì đoạn thẳng NP có độ dài ngắn nhất.
