Giải SGK Toán 8 KNTT Bài 14. Hình thoi và hình vuông có đáp án
-
127 lượt thi
-
18 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
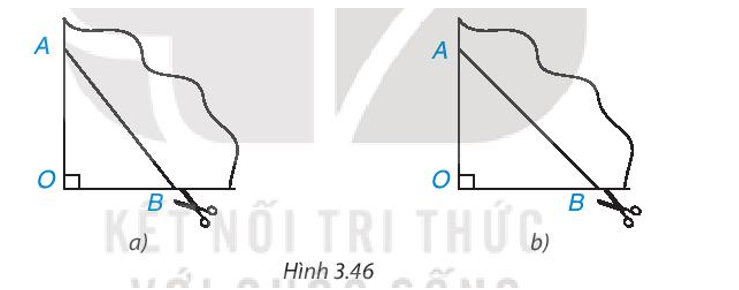
Lấy một tờ giấy, gấp làm tư tạo ra một góc vuông O, đánh dấu hai điểm A, B trên hai cạnh góc vuông rồi cắt theo đoạn thẳng AB (H.3.46a). Sau khi mở tờ giấy ra, ta được một tứ giác. Tứ giác đó là hình gì? Vì sao? Nếu ta có OA = OB thì tứ giác nhận được là hình gì (H.3.46b)?
 Xem đáp án
Xem đáp án
Sau bài học này ta giải quyết được bài toán như sau:
• Hình 3.46a)
Khi gấp làm tư tạo ra một góc vuông O, đánh dấu hai điểm A, B trên hai cạnh góc vuông thì tạo ra tứ giác có bốn cạnh bằng nhau và đều bằng cạnh AB.
Khi đó, tứ giác ABCD là hình thoi.
• Hình 3.46b)
Khi gấp làm tư tạo ra một góc vuông O, đánh dấu hai điểm A, B trên hai cạnh góc vuông. Nếu OA = OB thì hai đường chéo của tứ giác bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
Khi đó, tứ giác đã cho là hình vuông.
Câu 2:
Hình thoi có phải là hình bình hành không? Nếu có, từ tính chất đã biết của hình bình hành, hãy suy ra những tính chất tương ứng của hình thoi.
 Xem đáp án
Xem đáp án
Hình thoi có bốn cạnh bằng nhau nên ta suy ra hai cặp cạnh đối bằng nhau.
Ta suy ra tính chất hình thoi dựa vào tính chất của hình bình hành như sau:
- Hình thoi có hai góc đối bằng nhau.
- Hình thoi có các cặp cạnh đối song song.
- Hình thoi có hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Câu 3:
Cho hình thoi ABCD có hai đường chéo AC, BD cắt nhau tại O (H.3.48).
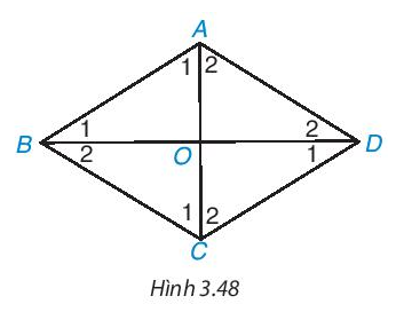
a) ∆ABD có cân tại A không?
 Xem đáp án
Xem đáp án
a) Vì tứ giác ABCD là hình thoi nên AB = AD.
Suy ra ∆ABD có cân tại A.
Câu 4:
b) AC có vuông góc với BD không và AC có là đường phân giác của góc A không? Vì sao?
 Xem đáp án
Xem đáp án
b) Vì tứ giác ABCD là hình thoi nên AB = BC = CD = DA.
Xét ∆ABC và ∆ADC có:
AB = AD (chứng minh trên);
BC = CD (chứng minh trên);
Cạnh AC chung.
Do đó ∆ABC = ∆ADC (c.c.c)
Suy ra (hai góc tương ứng)
Hay AC là đường phân giác của góc A.
Tam giác ABD cân tại A có AO là đường phân giác của góc A (vì AC là đường phân giác góc A) nên AO cũng là đường cao.
Khi đó AO ⊥ BD hay AC ⊥ BD.
Vậy AC vuông góc với BD và AC là đường phân giác của góc A.
Câu 5:
Hãy viết giả thiết, kết luận của câu c trong Định lí 2.
 Xem đáp án
Xem đáp án
Giả thiết, kết luận của Định lí 2.
a)
|
GT |
Hình bình hành ABCD có AB = BC. |
|
KL |
ABCD là hình thoi. |
Ta có thể viết giả thiết đối với các cặp cạnh kề khác, chẳng hạn như:
Hình bình hành ABCD có BC = CD hoặc CD = DA hoặc DA = AB.
b)
|
GT |
Hình bình hành ABCD có AC ⊥ BD. |
|
KL |
ABCD là hình thoi. |
c)
|
GT |
Hình bình hành ABCD có . |
|
KL |
ABCD là hình thoi. |
Ta có thể viết giả thiết tương tự đối với tia phân giác góc B hoặc góc C hoặc góc D.
Câu 6:
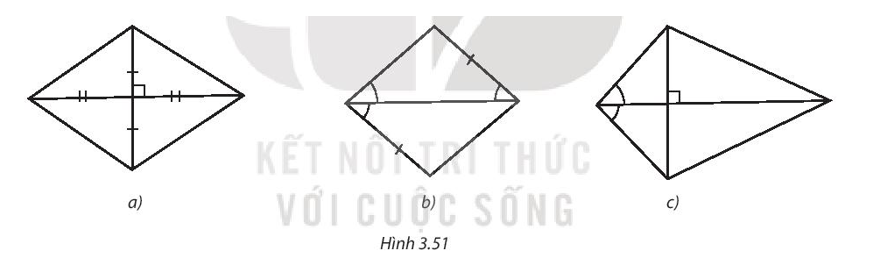
Trong Hình 3.51, hình nào là hình thoi? Vì sao?
 Xem đáp án
Xem đáp án
• Hình 3.51a)
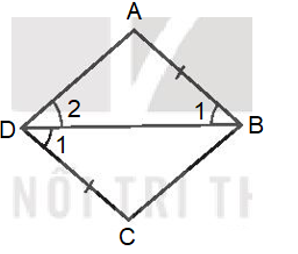
Tứ giác đã cho có hai đường chéo cắt nhau tại trung điểm của mỗi đường và chúng vuông góc với nhau nên tứ giác đó là hình thoi.
• Gọi tứ giác trong Hình 3.51b) là tứ giác ABCD.
Vì mà hai góc này ở vị trí so le trong nên AB // CD.
Mà AB = CD nên tứ giác ABCD là hình bình hành.
Mặt khác, hay DB là tia phân giác của .
Khi đó, hình bình hành ABCD có DB là tia phân giác của .
Do đó tứ giác ABCD là hình thoi.
• Tứ giác trong Hình 3.51c) hai đường chéo vuông góc với nhau và có đường chéo là đường vuông góc của một góc của tứ giác.
Từ đó ta suy ra tứ giác đã cho không phải là hình thoi.
Vậy Hình 3.51a và Hình 3.51b là hình thoi.
Câu 7:
Hãy giải thích tại sao hai đường chéo của hình vuông bằng nhau và vuông góc với nhau.
 Xem đáp án
Xem đáp án
Hình vuông cũng là hình thoi, hình chữ nhật.
Mà hình chữ nhật có hai đường chéo bằng nhau còn hình thoi có hai đường chéo vuông góc với nhau.
Do đó, hai đường chéo của hình vuông bằng nhau và vuông góc với nhau.
Câu 8:
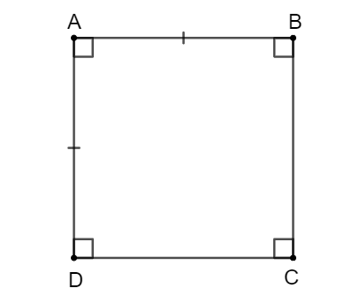
Hãy viết giả thiết, kết luận của câu a trong Định lí 4.
 Xem đáp án
Xem đáp án
|
GT |
Hình chữ nhật ABCD có AB = AD. |
|
KL |
ABCD là hình vuông. |
Ta có thể viết giả thiết đối với cặp cạnh kề khác như: AB = BC; BC = CD; CD = AD.
Câu 9:
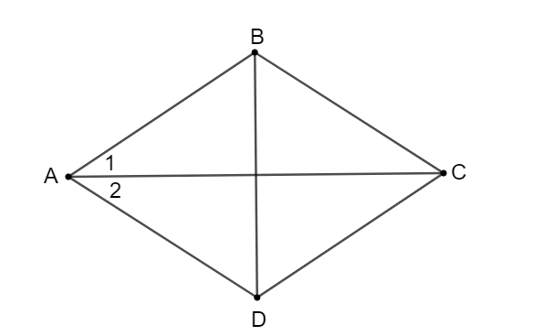
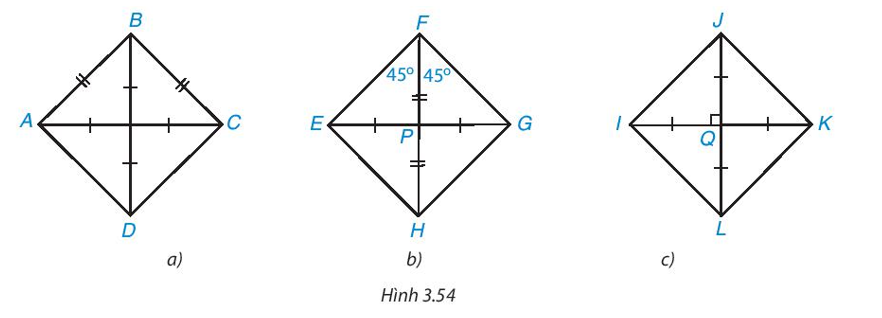
Với mỗi hình dưới đây, ta dùng dấu hiệu nhận biết nào để khẳng định đó là hình vuông?
 Xem đáp án
Xem đáp án
• Hình 3.54a)
Tứ giác ABCD có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.
Suy ra tứ giác này là hình chữ nhật.
Mà AB = BC nên tứ giác ABCD là hình vuông.
Ta dùng dấu hiệu nhận biết: Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
• Hình 3.54b)
Tứ giác EFGH có hai đường chéo cắt nhau tại trung điểm P của mỗi đường.
Ta có .
Suy ra tứ giác EFGH là hình chữ nhật.
Hình chữ nhật EFGH có đường chéo FH là đường phân giác của .
Do đó tứ giác EFGH là hình vuông.
Ta dùng dấu hiệu nhận biết: Hình chữ nhật có một đường chéo là đường phân giác của một góc của hình vuông.
• Hình 3.54c)
Tứ giác IJKL có hai đường chéo IK và JL bằng nhau và cắt nhau tại trung điểm Q của mỗi đường.
Suy ra tứ giác IJKL là hình chữ nhật.
Mà IK ⊥ JL nên tứ giác IJKL là hình vuông.
Ta dùng dấu hiệu nhận biết: Hình chữ nhật có hai đường chéo vuông góc là hình chữ nhật.
Câu 10:
Lấy một tờ giấy, gấp làm tư tạo ra một góc vuông O, đánh dấu hai điểm A, B trên hai cạnh góc vuông rồi cắt theo đoạn thẳng AB (H.3.46a). Sau khi mở tờ giấy ra, ta được một tứ giác. Tứ giác đó là hình gì? Vì sao? Nếu ta có OA = OB thì tứ giác nhận được là hình gì (H.3.46b)?
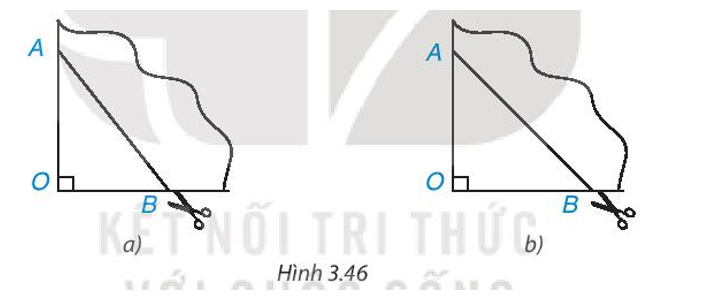
Hãy giải thích tại sao.
- Trong trường hợp a, ta được hình thoi.
- Trong trường hợp b, ta được hình vuông Xem đáp án
Xem đáp án
- Trong trường hợp a:
Khi gấp làm tư tạo ra một góc vuông O, đánh dấu hai điểm A, B trên hai cạnh góc vuông thì tạo ra tứ giác có bốn cạnh bằng nhau và đều bằng cạnh AB.
Khi đó, tứ giác ABCD là hình thoi.
- Trong trường hợp b:
Khi gấp làm tư tạo ra một góc vuông O, đánh dấu hai điểm A, B trên hai cạnh góc vuông. Nếu OA = OB thì hai đường chéo của tứ giác bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
Khi đó, tứ giác đã cho là hình vuông.
Câu 11:
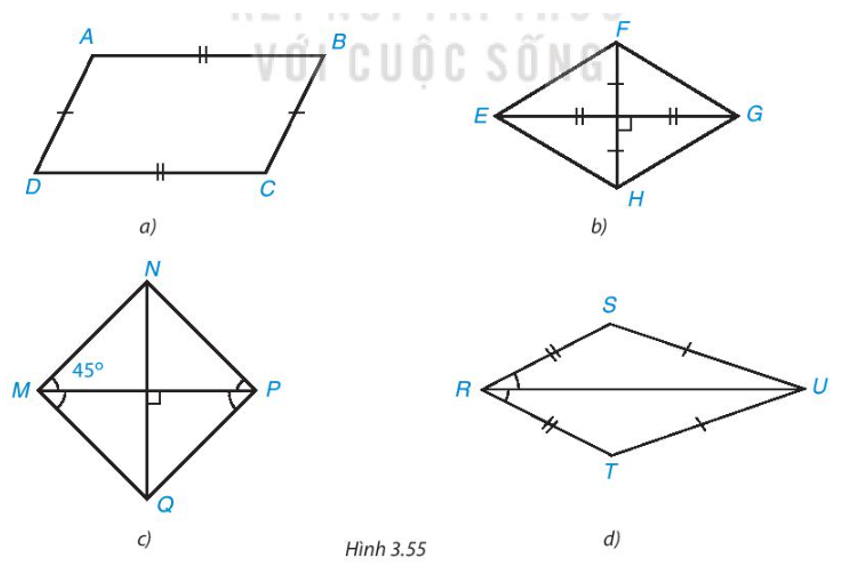
Tìm hình thoi và hình vuông trong Hình 3.55.
 Xem đáp án
Xem đáp án
* Xét Hình 3.55a)
Tứ giác ABCD có AB = CD; AD = BC.
Suy ra tứ giác ABCD là hình bình hành.
* Xét Hình 3.55b)
Tứ giác EFGH có hai đường chéo EG và FH cắt nhau tại trung điểm của mỗi đường.
Suy ra tứ giác EFGH là hình bình hành.
Hình bình hành EFGH có hai đường chéo vuông góc với nhau
Do đó tứ giác EFGH là hình thoi.
Câu 12:
Cho tam giác ABC, D là một điểm nằm giữa B và C. Qua D kẻ các đường thẳng song song với AB, AC, chúng cắt các cạnh AC, AB lần lượt tại E, F.
a) Tứ giác AEDF là hình gì? Vì sao?
 Xem đáp án
Xem đáp án
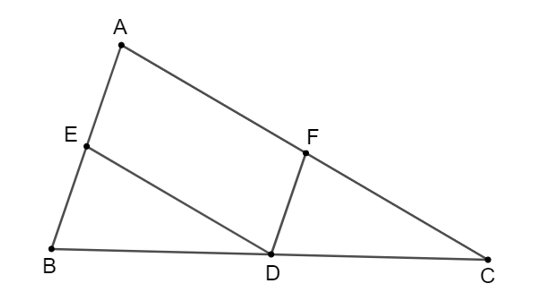
a) Tứ giác AEDF có AE // DF; AF // DE (giả thiết).
Suy ra tứ giác AEDF là hình bình hành.
Câu 13:
b) Nếu tam giác ABC cân tại A thì điểm D ở vị trí nào trên cạnh BC để tứ giác AEDF là hình thoi?
 Xem đáp án
Xem đáp án
b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A.
Vậy nếu D là giao điểm của tia phân giác góc A với cạnh BC thì AEDF là hình thoi.
Câu 14:
c) Nếu tam giác ABC vuông tại A thì tứ giác AEDF là hình gì?
 Xem đáp án
Xem đáp án
c) Nếu ΔABC vuông tại A thì AEDF là hình chữ nhật (vì hình vuông là hình bình hành có một góc vuông).
Câu 15:
d) Nếu tam giác ABC vuông cân tại A thì điểm D ở vị trí nào trên cạnh BC để AEDF là hình vuông?
 Xem đáp án
Xem đáp án
d) Nếu ABC vuông tại A và D là giao điểm của tia phân giác của góc A với cạnh BC thì AEDF là hình vuông (vì hình vuông vừa là hình chữ nhật, vừa là hình thoi).
Câu 16:
Chứng minh rằng các trung điểm của bốn cạnh trong một hình chữ nhật là các đỉnh của một hình thoi.
 Xem đáp án
Xem đáp án
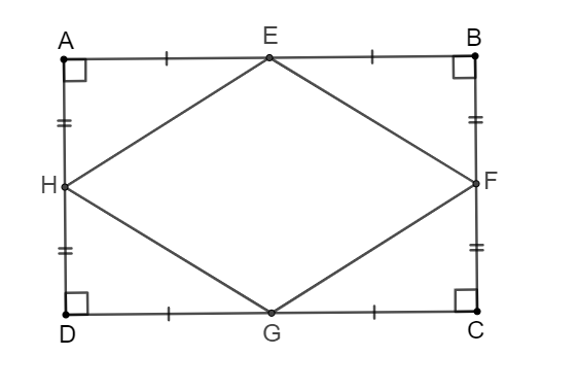
Xét tam giác ABD có E và H lần lượt là trung điểm của AB và AD.
Suy ra EH là đường trung bình của tam giác ABD.
Do đó (1)
Chứng minh tương tự, ta có: (2)
Lại có, ABCD là hình chữ nhật nên AC = BD (3)
Từ (1), (2) và (3) suy ra EF = FG = GH = HE.
Do đó tứ giác ABCD là hình thoi.
Câu 17:
Chứng minh rằng các trung điểm của bốn cạnh trong một hình thoi là các đỉnh của một hình chữ nhật.
 Xem đáp án
Xem đáp án
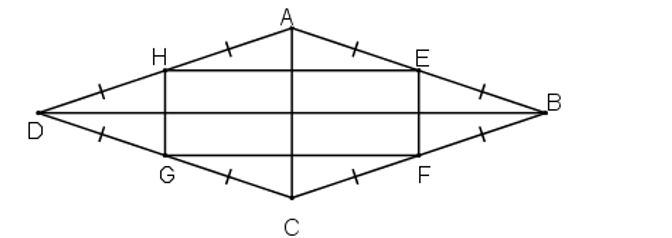
Xét tam giác ABC có E và F lần lượt là trung điểm của AB và BC.
Suy ra EF là đường trung bình của tam giác ABC.
Do đó EF // AC và (1)
* Tương tự tam giác ADC có HG là đường trung bình nên:
HG // AC và (2)
Từ (1) và (2) suy ra: EF // HG và EF = HG.
Suy ra tứ giác EFGH là hình bình hành.
Lại có: EF // AC và BD ⊥ AC nên BD ⊥ EF.
EH // BD và EF ⊥ BD nên EF ⊥ EH.
Nên .
Hình bình hành EFGH có nên là hình chữ nhật.
Câu 18:
Cho hình chữ nhật ABCD có chu vi bằng 36 cm. Gọi M là trung điểm của cạnh BC. Biết rằng MA ⊥ MD. Tính độ dài các cạnh của hình chữ nhật ABCD (H.3.56).
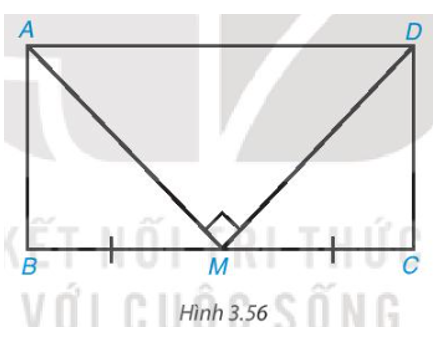
 Xem đáp án
Xem đáp án
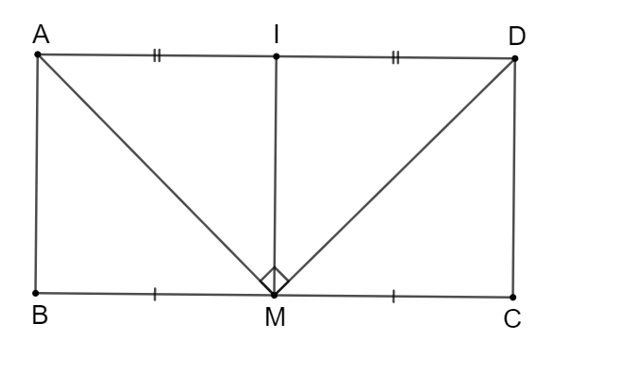
Gọi I là trung điểm của AD.
Khi đó, mà M là trung điểm của BC nên MI = AB.
Suy ra nên AD = 2AB.
Mà (cm).
Suy ra AB + 2AB = 18
Hay 3AB = 18
Do đó AB = 6 (cm).
Suy ra AD = 2AB = 2 . 6 = 12 (cm).
Vậy độ dài các cạnh của hình chữ nhật ABCD là AB = CD = 6 cm; AD = BC = 12 cm.
