Giải SGK Toán 8 KNTT Bài 16. Đường trung bình của tam giác có đáp án
-
205 lượt thi
-
12 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
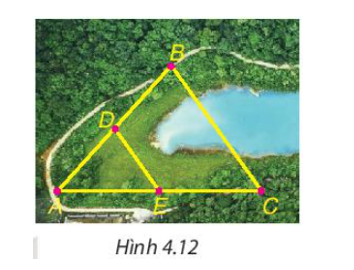
Cho B và C là hai điểm cách nhau bởi một hồ nước như Hình 4.12 với D, E lần lượt là trung điểm của AB và AC. Biết DE = 500 m, liệu không cần đo trực tiếp, ta có thể tính được khoảng cách giữa hai điểm B và C không?
 Xem đáp án
Xem đáp án
Sau bài học này ta giải quyết được bài toán như sau:
Trong tam giác ABC có D, E lần lượt là trung điểm của AB và AC nên D ∈ AB; E ∈ AC và AD = BD; AE = EC.
Suy ra DE là đường trung bình của tam giác ABC.
Do đó suy ra BC = 2DE = 2 . 500 = 1 000 (m)
Vậy khoảng cách giữa hai điểm B và C bằng 1 000 m.
Câu 2:
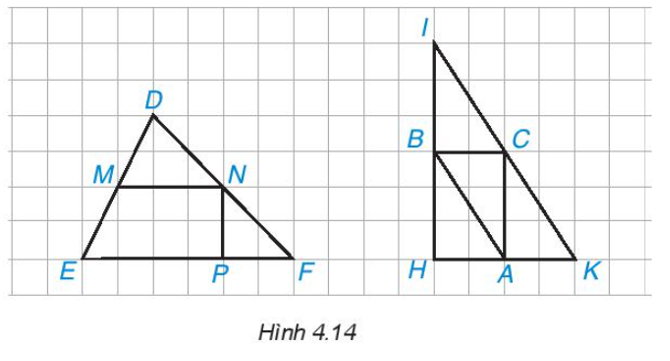
Em hãy chỉ ra các đường trung bình của ∆DEF và ∆IHK trong Hình 4.14.
 Xem đáp án
Xem đáp án
Quan sát Hình 4.14, ta thấy:
* Xét ∆DEF có M là trung điểm của cạnh DE; N là trung điểm của cạnh DF nên MN là đường trung bình của ∆DEF.
* Xét ∆IHK có:
• B là trung điểm của cạnh IH; C là trung điểm của cạnh IK nên BC là đường trung bình của ∆DEF.
• B là trung điểm của cạnh IH; A là trung điểm của cạnh HK nên AB là đường trung bình của ∆DEF.
• A là trung điểm của cạnh HK; C là trung điểm của cạnh IK nên AC là đường trung bình của ∆DEF.
Vậy đường trung bình của ∆DEF là MN; các đường trung bình của ∆IHK là AB, BC, AC.
Câu 3:
Cho DE là đường trung bình của tam giác ABC (H.4.15
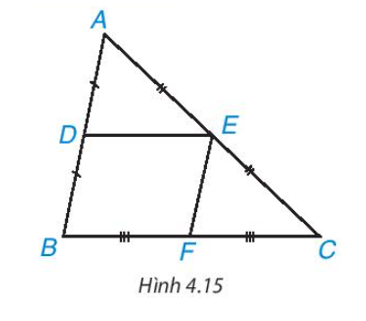
Sử dụng định lí Thalès đảo, chứng minh rằng DE // BC.
 Xem đáp án
Xem đáp án
Ta có AD = BD và D ∈ AB nên D là trung điểm của AB;
AE = EC và E ∈ AC nên E là trung điểm của AC.
Xét tam giác ABC có D, E lần lượt là trung điểm của AB và AC, theo định lí Thalès đảo, ta suy ra DE // BC (đpcm).
Câu 4:
Cho DE là đường trung bình của tam giác ABC (H.4.15
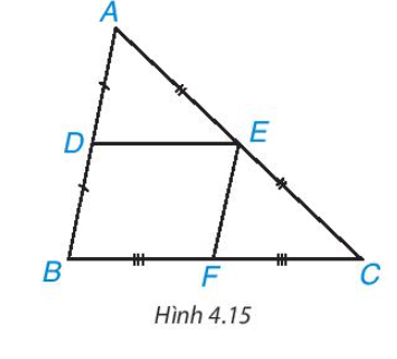
Gọi F là trung điểm của BC. Chứng minh tứ giác DEFB là hình bình hành. Từ đó suy ra .
 Xem đáp án
Xem đáp án
Vì DE là đường trung bình của tam giác ABC nên D, E lần lượt là trung điểm của AB, AC.
Suy ra .
Do đó DE // BC (theo định lí Thalès đảo).
Vì E, F lần lượt là trung điểm của AC, BC.
Suy ra .
Do đó EF // AB (theo định lí Thalès đảo).
Xét tứ giác DEFB có DE // BF (vì DE // BC); EF // BD (vì EF // AB)
Do đó tứ giác DEFB là hình bình hành.
Suy ra DE = BF mà nên .
Câu 5:
Cho tam giác ABC cân tại A, D và E lần lượt là trung điểm của AB, AC. Tứ giác DECB là hình gì? Tại sao?
 Xem đáp án
Xem đáp án
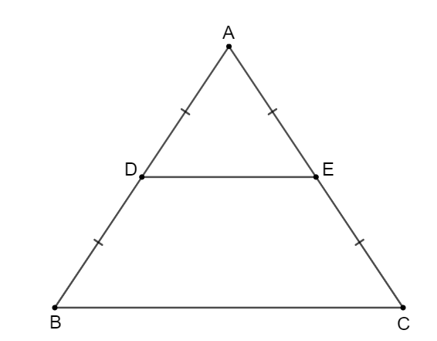
Tam giác ABC cân tại A nên .
Vì D và E lần lượt là trung điểm của AB, AC nên DE là đường trung bình của tam giác ABC.
Suy ra DE // BC nên tứ giác DECB là hình thang.
Hình thang DECB có nên tứ giác DECB là hình thang cân.
Câu 6:
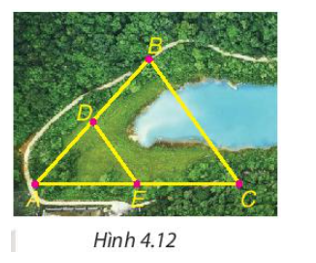
Cho B và C là hai điểm cách nhau bởi một hồ nước như Hình 4.12 với D, E lần lượt là trung điểm của AB và AC. Biết DE = 500 m, liệu không cần đo trực tiếp, ta có thể tính được khoảng cách giữa hai điểm B và C không?
 Xem đáp án
Xem đáp án
Trong tam giác ABC có D, E lần lượt là trung điểm của AB và AC nên D ∈ AB; E ∈ AC và AD = BD; AE = EC.
Suy ra DE là đường trung bình của tam giác ABC.
Do đó suy ra BC = 2DE = 2 . 500 = 1 000 (m)
Vậy khoảng cách giữa hai điểm B và C bằng 1 000 m.
Câu 7:
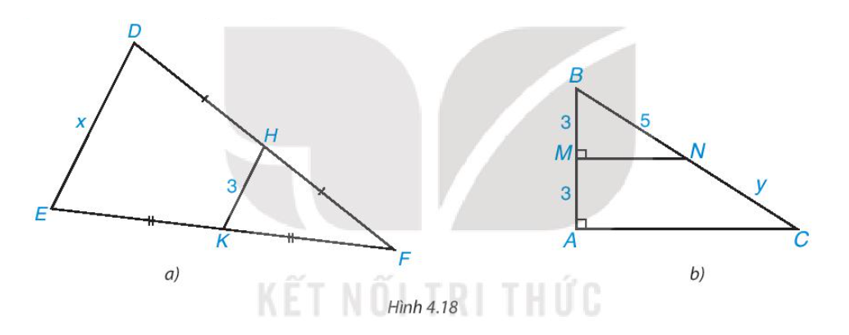
Tính các độ dài x, y trong Hình 4.18.
 Xem đáp án
Xem đáp án
• Hình 4.18a)
Ta có: DH = HF, H ∈ DF nên H là trung điểm của DF;
EK = KF, K ∈ EF nên K là trung điểm của EF.
Xét tam giác DEF có H, K lần lượt là trung điểm của DF, EF nên HK là đường trung bình của tam giác DEF.
Suy ra .
Do đó x = 2HK = 2 . 3 = 6.
• Hình 4.18b)
Vì MN ⊥ AB, AC ⊥ AB nên MN // AC.
Mà M là trung điểm của BC (vì AM = BM = 3)
Suy ra MN là đường trung bình của tam giác ABC.
Do đó y = NC = BN = 5.
Vậy x = 6; y = 5.
Câu 8:
Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC.
a) Chứng minh tứ giác BMNC là hình thang.
 Xem đáp án
Xem đáp án
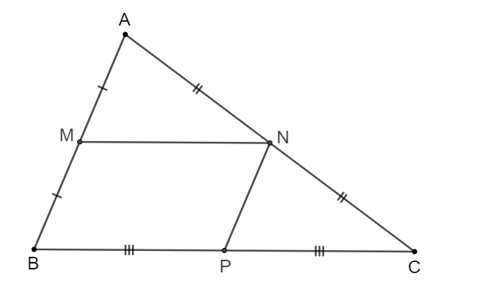
a) Vì M, N lần lượt là trung điểm của các cạnh AB, AC nên MN là đường trung bình của tam giác ABC suy ra MN // BC hay MN // BP.
Tứ giác BMNC có MN // BP nên tứ giác BMNC là hình thang (đpcm).
Câu 9:
b) Tứ giác MNPB là hình gì? Tại sao?
 Xem đáp án
Xem đáp án
b) Vì N, P lần lượt là trung điểm của các cạnh AC, BC nên NP là đường trung bình của tam giác ABC suy ra NP // AB hay NP // MB.
Tứ giác MNPB có MN // BP; BM // NP (chứng minh trên).
Do đó, tứ giác MNPB là hình bình hành.
Câu 10:
Cho tam giác ABC có trung tuyến AM. Lấy điểm D và E trên cạnh AB sao cho AD = DE = EB và D nằm giữa hai điểm A, E.
a) Chứng minh DC // EM.
 Xem đáp án
Xem đáp án
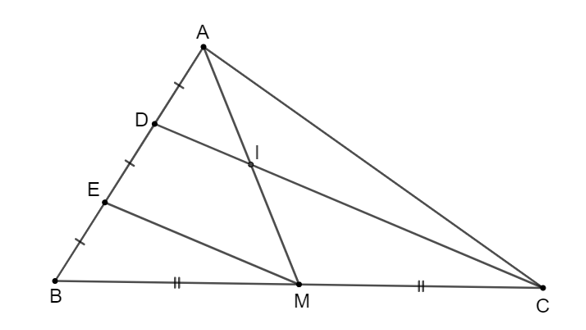
a) Vì AM là đường trung tuyến của tam giác ABC nên M là trung điểm của BC.
Ta có BE = DE và E ∈ BD nên E là trung điểm của BD.
Xét tam giác BCD có E, M lần lượt là trung điểm của BD, BC nên EM là đường trung bình của tam giác BCD.
Do đó DC // EM (tính chất đường trung bình).
Câu 11:
 Xem đáp án
Xem đáp án
b) Ta có D là trung điểm của AE (vì AD = DE, D ∈ AE).
Mà DI // EM (vì DC // EM).
Do đó DI là đường trung bình của tam giác AEM.
Suy ra I là trung điểm của AM.
Câu 12:
Cho hình chữ nhật ABCD có AC cắt BD tại O. Gọi H, K lần lượt là trung điểm của AB, AD. Chứng minh tứ giác AHOK là hình chữ nhật.
 Xem đáp án
Xem đáp án
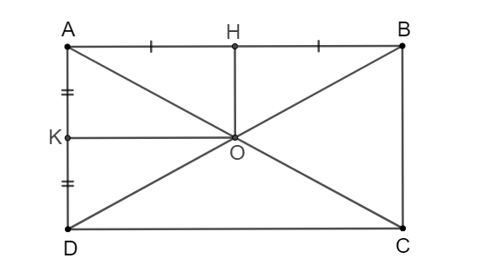
Vì ABCD là hình chữ nhật nên và hai đường chéo AC, BD bằng nhau và cắt nhau tại trung điểm O của mỗi đường.
Suy ra AB ⊥ AD; O là trung điểm của AC và BD.
Vì O, H lần lượt là trung điểm của BD và AB nên OH là đường trung bình của tam giác ABD.
Suy ra OH // AD mà AB ⊥ AD nên OH ⊥ AB hay .
Tương tự, ta chứng minh được: OK ⊥ AD hay .
Ta có:
Suy ra .
Tứ giác AHOK có .
Do đó, tứ giác AHOK là hình chữ nhật.
