Giải SGK Toán 8 KNTT Bài 9. Phân tích đa thức thành nhân tử có đáp án
-
145 lượt thi
-
21 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Tròn nói: Tớ biết cách tìm được tất cả số x để 2x2 + x = 0.
Vuông thắc mắc: Tròn làm như thế nào nhỉ?
 Xem đáp án
Xem đáp án
Sau bài học này ta giải quyết được bài toán như sau:
Để tìm x thỏa mãn 2x2 + x = 0 thì Tròn cần phân tích đa thức 2x2 + x thành nhân tử.
Ta có: 2x2 + x = x(2x + 1) (phân tích đa thức thành nhân tử bằng cách đặt nhân tử chung).
Khi đó x(2x + 1) = 0
x = 0 hoặc 2x + 1 = 0
x = 0 hoặc .
Vậy .
Câu 2:
Hãy viết đa thức x2 – 2xy thành tích của các đa thức, khác đa thức là số.
 Xem đáp án
Xem đáp án
Áp dụng tính chất phân phối giữa phép nhân với phép cộng, ta viết đa thức x2 – 2xy thành tích của các đa thức như sau:
x2 – 2xy = x(x – 2y).
Câu 4:
 Xem đáp án
Xem đáp án
Câu 5:
Giải bài toán mở đầu bằng cách phân tích 2x2 + x thành nhân tử.
 Xem đáp án
Xem đáp án
Để tìm x thỏa mãn 2x2 + x = 0 thì Tròn cần phân tích đa thức 2x2 + x thành nhân tử.
Ta có: 2x2 + x = x(2x + 1) (phân tích đa thức thành nhân tử bằng cách đặt nhân tử chung).
Khi đó x(2x + 1) = 0
x = 0 hoặc 2x + 1 = 0
x = 0 hoặc .
Vậy .
Câu 6:
Phân tích các đa thức sau thành nhân tử
a) (x + 1)2 – y2;
 Xem đáp án
Xem đáp án
a) (x + 1)2 – y2 = (x + 1 + y)(x + 1 – y);
Câu 7:
b) x3 + 3x2 + 3x + 1;
 Xem đáp án
Xem đáp án
b) x3 + 3x2 + 3x + 1 = x3 + 3 . x2 . 1 + 3 x . 12 + 13 = (x + 1)3;
Câu 8:
c) 8x3 – 12x2 + 6x – 1.
 Xem đáp án
Xem đáp án
c) 8x3 – 12x2 + 6x – 1 = (2x)3 – 3. (2x)2 . 1 + 3 . 2x . 12 – 13 = (2x – 1)3.
Câu 9:
Phân tích các đa thức 2x2 – 4xy + 2y – x thành nhân tử.
 Xem đáp án
Xem đáp án
Ta phân tích các đa thức 2x2 – 4xy + 2y – x thành nhân tử như sau:
2x2 – 4xy + 2y – x = (2x2 – 4xy) + (2y – x)
= 2x(x – 2y) + (2y – x) = –2x(2y – x) + (2y – x)
= (2y – x)(1 – 2x).
Câu 10:
Tính nhanh giá trị của biểu thức
A = x2 + 2y – 2x – xy tại x = 2022, y = 2020.
 Xem đáp án
Xem đáp án
Ta có A = x2 + 2y – 2x – xy = (x2 – 2x) + (2y – xy)
= x(x – 2) + y(2 – x) = x(x – 2) – y(x – 2)
= (x – 2)(x – y).
Thay x = 2022, y = 2020 vào biểu thức A, ta được:
(2022 – 2)(2022 – 2020) = 2020 . 2 = 4040.
Câu 11:
Phân tích x3 – x thành nhân tử
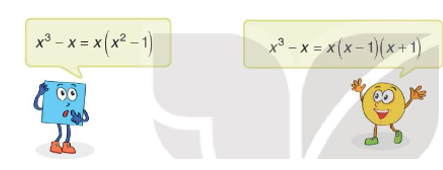
Em hãy nêu ý kiến của em về lời giải của Tròn và Vuông.
 Xem đáp án
Xem đáp án
Bạn Vuông phân tích đa thức đã cho thành tích của hai đa thức, tuy nhiên đa thức trong ngoặc còn có thể phân tích tiếp được.
Bạn Tròn phân tích đa thức thành các nhân tử, trong đó mỗi nhân tử không phân tích tiếp được nữa.
Câu 13:
Phân tích các đa thức sau thành nhân tử:
b) 6a2b – 18ab;
 Xem đáp án
Xem đáp án
b) 6a2b – 18ab = 6ab(a – 3);
Câu 14:
Phân tích các đa thức sau thành nhân tử:
c) x3 – 4x;
 Xem đáp án
Xem đáp án
c) x3 – 4x = x(x2 – 4) = x(x + 2)(x – 2);
Câu 15:
Phân tích các đa thức sau thành nhân tử:
d) x4 – 8x.
 Xem đáp án
Xem đáp án
d) x4 – 8x = x(x3 – 8) = x(x3 – 23)
= x(x – 2)(x2 + 2x + 22)
= x(x – 2)(x2 + 2x + 4).
Câu 16:
Phân tích các đa thức sau thành nhân tử:
a) x2 – 9 + xy + 3y;
 Xem đáp án
Xem đáp án
a) x2 – 9 + xy + 3y = (x2 – 9) + (xy + 3y)
= (x + 3)(x – 3) + y(x + 3)
= (x + 3)(x + y – 3).
Câu 17:
Phân tích các đa thức sau thành nhân tử:
b) x2y + x2 + xy – 1.
 Xem đáp án
Xem đáp án
b) x2y + x2 + xy – 1 = (x2y + xy) + (x2 – 1)
= xy(x + 1) + (x + 1)(x – 1) = (x + 1)(xy + x – 1).
Câu 18:
Tìm x, biết:
a) x2 – 4x = 0;
 Xem đáp án
Xem đáp án
a) x2 – 4x = 0
x(x – 4) = 0
x = 0 hoặc x – 4 = 0
x = 0 hoặc x = – 4.
Vậy x ∈ {0; – 4}.
Câu 19:
Tìm x, biết:
b) 2x3 – 2x = 0.
 Xem đáp án
Xem đáp án
b) 2x3 – 2x = 0
2x(x2 – 1) = 0
2x(x + 1)(x – 1) = 0
x = 0 hoặc x + 1 = 0 hoặc x – 1 = 0
x = 0 hoặc x = – 1 hoặc x = 1.
Vậy x ∈ {– 1; 0; 1}.
Câu 20:
Một mảnh vườn hình vuông có độ dài cạnh bằng x (mét). Người ta làm đường đi xung quanh mảnh vườn, có độ rộng như nhau và bằng y (mét) (H.2.2).
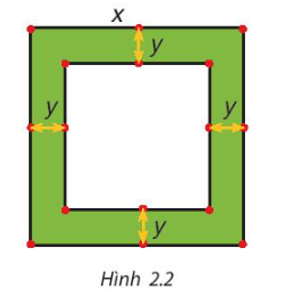
a) Viết biểu thức tính diện tích S của đường bao quanh mảnh vườn theo x và y.
 Xem đáp án
Xem đáp án
a) Đặt tên các điểm A, B, C, D, M, N, P, Q như hình vẽ.
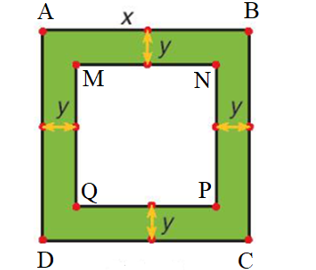
Diện tích hình vuông ABCD là: x2 (m).
Hình vuông ABCD có độ dài một cạnh là: x – y – y = x – 2y (m).
Diện tích hình vuông ABCD là: (x – 2y)2 (m).
Diện tích S của đường bao quanh mảnh vườn là:
S = x2 – (x – 2y)2 = (x + x – 2y)(x – x + 2y) = 2y(2x – 2y) = 4xy – 4y2 (m2).
Vậy diện tích S của đường bao quanh mảnh vườn là 4xy – 4y2 (m2).
Câu 21:
 Xem đáp án
Xem đáp án
b) Phân tích đa thức S thành nhân tử, ta được:
S = x2 – (x – 2y)2 = (x + x – 2y)(x – x + 2y) = 2y(2x – 2y).
Thay x = 102 m, y = 2 m vào biểu thức S, ta được:
S = 2y(2x – 2y) = 2 . 2 . (2 . 102 – 2 . 2) = 4 . (204 – 4) = 4 . 200 = 800 (m2).
