Giải SGK Toán 8 KNTT Luyện tập chung có đáp án
-
129 lượt thi
-
11 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho các biểu thức:
.
a) Trong các biểu thức đã cho, biểu thức nào là đơn thức? Biểu thức nào không là đơn thức?
 Xem đáp án
Xem đáp án
a) Các biểu thức là đơn thức.
Các biểu thức không là đơn thức.
Câu 2:
b) Hãy chỉ ra hệ số và phần biến của mỗi đơn thức đã cho.
 Xem đáp án
Xem đáp án
b) • Đơn thức có hệ số là và phần biến là x;
• Đơn thức có hệ số là và phần biến là xy;
• Đơn thức −3xy2 có hệ số là −3 và phần biến là xy2;
• Đơn thức có hệ số là và phần biến là x2y;
• Đơn thức có hệ số là và phần biến là x2y.
Câu 3:
c) Viết tổng tất cả các đơn thức trên để được một đa thức. Xác định bậc của đa thức đó.
 Xem đáp án
Xem đáp án
c) Tổng tất cả các đơn thức trên là:
.
Đa thức là 3.
Câu 4:
Trong một khách sạn có hai bể bơi dạng hình hộp chữ nhật. Bể thứ nhất có chiều sâu là 1,2 m, đáy là hình chữ nhật có chiều dài x mét, chiều rộng y mét. Bể thứ hai có chiều sâu 1,5 m, hai kích thước đáy gấp 5 lần hai kích thước đáy của bể thứ nhất.
a) Hãy tìm đơn thức (hai biến x và y) biểu thị số mét khối nước cần có để bơm đầy cả hai bể bơi.
 Xem đáp án
Xem đáp án
a) Bể thứ hai có đáy là hình chữ nhật có chiều dài 5x mét và chiều rộng là 5y mét.
Số mét khối nước cần có để bơm đầy cả hai bể bơi là thể tích nước chứa được ở hai bể bơi.
Câu 5:
 Xem đáp án
Xem đáp án
b) Biểu thức biểu thị số mét khối nước cần có để bơm đầy bể thứ nhất là: 1,2xy;
Biểu thức biểu thị số mét khối nước cần có để bơm đầy bể thứ hai là: 1,5 . 5x . 5y = 37,5xy;
Do đó, biểu thức biểu thị số mét khối nước cần có để bơm đầy cả hai bể bơi là:
1,2xy + 37,5xy = 38,7xy.
Câu 6:
Tìm bậc của mỗi đa thức sau rồi tính giá trị của chúng tại x = 1; y = −2.
P = 5x4 – 3x3y + 2xy3 – x3y + 2y4 – 7x2y2 – 2xy3;
Q = x3 + x2y – xy2 – x2y – xy2 – x3.
 Xem đáp án
Xem đáp án
• Ta có P = 5x4 – 3x3y + 2xy3 – x3y + 2y4 – 7x2y2 – 2xy3
= 5x4 – (3x3y + x3y) + (2xy3 – 2xy3) + 2y4 – 7x2y2
= 5x4 – 4x3y + 2y4 – 7x2y2.
Đa thức P có bậc là 4.
Thay x = 1; y = −2 vào biểu thức P, ta được:
P = 5 . 14 – 4 . 13 . (−2) + 2. (−2)4 – 7 . 12 . (−2)2
= 5 – 4 . (−2) + 2 . 16 – 7 . 4
= 5 + 8 + 32 – 28 = 13 + 4 = 17.
• Ta có Q = x3 + x2y – xy2 – x2y – xy2 – x3
= (x3 – x3) + (x2y – x2y) – (xy2 + xy2) = –2xy2.
Đa thức Q có bậc là 3.
Thay x = 1; y = −2 vào biểu thức Q, ta được:
Q = –2xy2 = –2 . 1 . (−2)2 = –2 . 4 = –8.
Câu 7:
Cho hai đa thức:
A = 7xyz2 – 5xy2z + 3x2yz – xyz + 1; B = 7x2yz – 5xy2z + 3xyz2 – 2.
a) Tìm đa thức C sao cho A – C = B;
 Xem đáp án
Xem đáp án
a) Ta có A – C = B
Suy ra C = A – B = (7xyz2 – 5xy2z + 3x2yz – xyz + 1) – (7x2yz – 5xy2z + 3xyz2 – 2)
= 7xyz2 – 5xy2z + 3x2yz – xyz + 1 – 7x2yz + 5xy2z – 3xyz2 + 2
= (7xyz2 – 3xyz2) + (5xy2z – 5xy2z) + (3x2yz – 7x2yz) – xyz + (1 + 2)
= 4xyz2 – 4x2yz – xyz + 3.
Vậy C = 4xyz2 – 4x2yz – xyz + 3.
Câu 8:
b) Tìm đa thức D sao cho A + D = B;
 Xem đáp án
Xem đáp án
b) Ta có A + D = B
Suy ra D = B – A = –(A – B) = –(4xyz2 – 4x2yz – xyz + 3)
= –4xyz2 + 4x2yz + xyz – 3.
Vậy D = –4xyz2 + 4x2yz + xyz – 3.
Câu 9:
 Xem đáp án
Xem đáp án
c) Ta có E – A = B.
Suy ra E = A + B = (7xyz2 – 5xy2z + 3x2yz – xyz + 1) + (7x2yz – 5xy2z + 3xyz2 – 2)
= 7xyz2 – 5xy2z + 3x2yz – xyz + 1 + 7x2yz – 5xy2z + 3xyz2 – 2
= (7xyz2 + 3xyz2) – (5xy2z + 5xy2z) + (7x2yz + 3x2yz) – xyz + (1 – 2)
= 10x2yz – 10xy2z + 10xyz2 – xyz + 3.
Vậy E = 10x2yz – 10xy2z + 10xyz2 – xyz + 3.
Câu 10:
Từ một miếng bìa, người ta cắt ra hai hình tròn có bán kính x centimét và y centimét. Tìm biểu thức biểu thị diện tích phần còn lại của miếng bìa, nếu biết miếng bìa có hình dạng gồm hai hình vuông ghép lại và có kích thước (centimét) như Hình 1.2. Biểu thức đó có phải là một đa thức không? Nếu phải thì đó là đa thức bậc mấy?
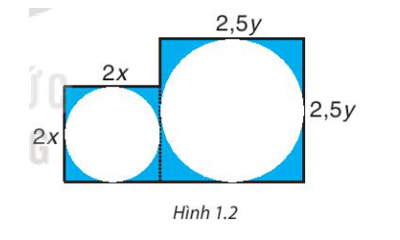
 Xem đáp án
Xem đáp án
Trong Hình 1.2 có:
• Diện tích hình vuông nhỏ là: (2x)2 = 4x2 (cm2).
Diện tích hình vuông lớn là: (2,5y)2 = 6,25y2 (cm2).
Tổng diện tích hai hình vuông là: 4x2 + 6,25y2 (cm2).
• Hình tròn nhỏ có đường kính là 2x nên sẽ có bán kính là x (cm)
Diện tích hình tròn nhỏ là: πx2 (cm2).
• Hình tròn lớn có đường kính là 2,5y nên sẽ có bán kính là 1,25y (cm)
Diện tích hình tròn lớn là: 1,5625πy2 (cm2).
Do đó, biểu thức biểu thị diện tích phần còn lại của miếng bìa là:
(4x2 + 6,25y2) – (πx2 + 1,5625πy2) = 4x2 + 6,25y2 – πx2 – 1,5625πy2
= (4x2 – πx2) + (6,25y2 – 1,5625πy2)
= (4 – π)x2 + (6,25 – 1,5625π)y2
Biểu thức (4 – π)x2 + (6,25 – 1,5625π)y2 là một đa thức bậc 2.
Câu 11:
Cho ba đa thức:
M = 3x3 – 4x2y + 3x – y; N = 5xy – 3x + 2; P = 3x3 + 2x2y + 7x – 1.
Tính M + N – P và M – N – P.
 Xem đáp án
Xem đáp án
Ta có:
• M + N – P = (3x3 – 4x2y + 3x – y) + (5xy – 3x + 2) – (3x3 + 2x2y + 7x – 1)
= 3x3 – 4x2y + 3x – y + 5xy – 3x + 2 – 3x3 – 2x2y – 7x + 1
= (3x3 – 3x3) – (4x2y + 2x2y) + 5xy + (3x – 3x – 7x) – y + (2 + 1)
= – 6x2y + 5xy – 7x – y + 3.
• M – N – P = (3x3 – 4x2y + 3x – y) – (5xy – 3x + 2) – (3x3 + 2x2y + 7x – 1)
= 3x3 – 4x2y + 3x – y + 5xy + 3x – 2 – 3x3 – 2x2y – 7x + 1
= (3x3 – 3x3) – (4x2y + 2x2y) + 5xy + (3x + 3x – 7x) – y + (1 – 2)
= – 6x2y + 5xy – x – y – 1.
Vậy M + N – P = – 6x2y + 5xy – 7x – y + 3; M – N – P = – 6x2y + 5xy – x – y – 1.
