Đề thi Học kì 1 Toán lớp 8 cực hay, có đáp án (Đề 4)
-
1051 lượt thi
-
5 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Phân tích đa thức thành nhân tử:
Xem đáp án
a) x2 + xy –x – y = x(x + y) – (x + y) = (x + y)(x -1 ).
b) a2 – b2 + 8a + 16 = (a2 + 8a + 16) – b2 = (a + 4)2 – b2
= (a + 4 – b)(a + 4 + b).
Câu 2:
Tìm x, biết:
Xem đáp án
a) 4x(x + 1) + (3 – 2x)(3 + 2x) = 15
⇔4x2 + 4x + (9 – 4x2) = 15
⇔ 4x2 + 4x + 9 – 4x2 = 15
⇔4x = 15 – 9
⇔4x = 6
⇔x = 3/2
b)3x(x – 20012) – x + 20012 = 0
⇔3x(x – 20012) – (x – 20012) = 0
⇔(x – 20012)(3x – 1) = 0
⇔x – 20012 = 0 hay 3x – 1 = 0
⇔x = 20012 hoặc x = 1/2
Câu 3:
Cho biểu thức:
a) Tìm điều kiện của x để biểu thức A xác định
b) Rút gọn biểu thức A
Xem đáp án
a) Ta có: x - 1 ≠ 0 ⇒ x ≠ 1
x2 - 1 = (x + 1)(x - 1) ≠ 0 ⇔ x ≠ -1 và x ≠ 1
x2 - 2x + 1 = (x - 1)2 ≠ 0 ⇔ x - 1 ≠ 0 ⇔ x ≠ 1
ĐKXĐ: x ≠ -1 và x ≠ 1
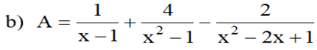
Câu 5:
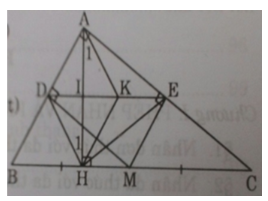
Cho tam giác ABC vuông tại A (AB < AC) . M là trung điểm cạnh BC. Vẽ MD vuông góc với AB tại D và ME vuông góc với AC tại E.
a) Chứng minh tứ giác ADME là hình chữ nhật.
b) Chứng minh E là trung điểm của đoạn thẳng AC và tứ giác CMDE là hình bình hành.
c) Vẽ đường cao AH của tam giác ABC. Chứng minh tứ giác MHDE là hình thang cân
d) Qua A vẽ đường thẳng song song với DH cắt DE tại K. Chứng minh HK vuông góc với AC.
Xem đáp án
a) Xét tứ giác ADME có:
∠(DAE) = ∠(ADM) = ∠(AEM) = 90o
⇒ Tứ giác ADME là hình chữ nhật (có ba góc vuông).
b) Ta có ME // AB ( cùng vuông góc AC)
M là trung điểm của BC (gt)
⇒ E là trung điểm của AC.
Ta có E là trung điểm của AC (cmt)
Chứng minh tương tự ta có D là trung điểm của AB
Do đó DE là đường trung bình của ΔABC
⇒ DE // BC và DE = BC/2 hay DE // MC và DE = MC
⇒ Tứ giác CMDE là hình bình hành.
c) Ta có DE // HM (cmt) ⇒ MHDE là hình thang (1)
Lại có HE = AC/2 (tính chất đường trung tuyến của tam giác vuông AHC)
DM = AC/2 (DM là đường trung bình của ΔABC) ⇒ HE = DM (2)
Từ (1) và (2) ⇒ MHDE là hình thang cân.
d) Gọi I là giao điểm của AH và DE. Xét ΔAHB có D là trung điểm của AB, DI // BH (cmt) ⇒ I là trung điểm của AH
Xét ΔDIH và ΔKIA có
IH = IA
∠DIH = ∠AIK (đối đỉnh),
∠H1 = ∠A1(so le trong)
ΔDIH = ΔKIA (g.c.g)
⇒ ID = IK
Tứ giác ADHK có ID = IK, IA = IH (cmt) ⇒ DHK là hình bình hành
⇒ HK // DA mà DA ⊥ AC ⇒ HK ⊥ AC