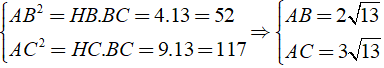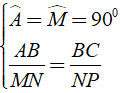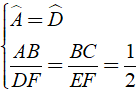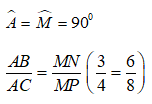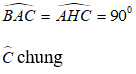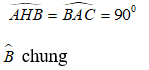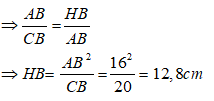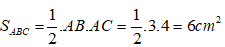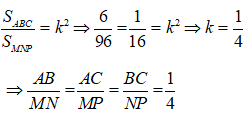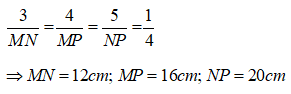Trắc nghiệm Các trường hợp đồng dạng của tam giác vuông (có đáp án)
-
802 lượt thi
-
17 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho tam giác vuông ABC vuông tại A, chân đường cao AH của tam giác ABC chia cạnh huyền BC thành hai đoạn thẳng BH = 4cm, HC = 9cm. Tính diện tích tam giác ABC?
 Xem đáp án
Xem đáp án
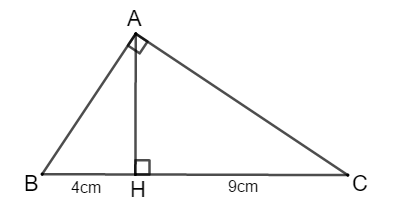
Ta có:
Vậy
Chọn đáp án A.
Câu 2:
Cho ΔABC và ΔMNP có , AB/MN = BC/NP thì?
 Xem đáp án
Xem đáp án
Xét ΔABC và ΔMNP, ta có:
⇒ Δ ABC ∼ Δ MNP ( c - g - c )
Chọn đáp án C.
Câu 3:
Nếu hai tam giác đồng dạng với nhau thì: Chọn phát biểu sai trong các phát biểu sau?
 Xem đáp án
Xem đáp án
Áp dụng tính chất mở rộng
Nếu hai tam giác đồng dạng với nhau thì:
+ Tỉ số hai đường cao tương ứng bằng tỉ số đồng dạng.
+ Tỉ số hai đường phân giác tương ứng bằng tỉ số đồng dạng.
+ Tỉ số hai đường trung tuyến tương ứng bằng tỉ số đồng dạng.
+ Tỉ số các chu vi bằng tỉ số đồng dạng.
Đáp án D sai.
Chọn đáp án D.
Câu 4:
Cho hai tam giác ABC và DEF có ,AB = 3cm, BC = 5cm,EF = 10cm, DF = 6cm. Chọn phát biểu đúng trong các phát biểu sau?
 Xem đáp án
Xem đáp án
Ta có:
⇒ Δ ABC ∼ Δ DFE ( c - g - c )
Chọn đáp án C.
Câu 5:
Cho tam giác ABC có AB = 3cm; AC = 4cm và BC = 5cm. Tam giác MNP vuông tại M có MN = 6cm; MP = 8cm. Tìm khẳng định sai
 Xem đáp án
Xem đáp án
Ta có:
Suy ra: tam giác ABC vuông tại A
Xét Δ ABC và Δ MNP có:
Suy ra: Δ ABC và ΔMNP đồng dạng với nhau.
Áp dụng định lí Pyta go vào tam giác MNP có:
nên NP = 10cm
Chọn đáp án D
Câu 6:
Cho tam giác ABC vuông tại A, kẻ AH vuông góc BC. Tìm tam giác đồng dạng với tam giác ABC?
 Xem đáp án
Xem đáp án
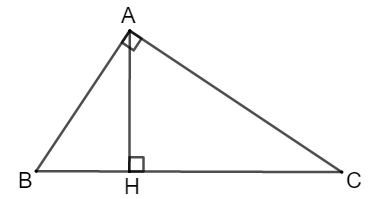
Xét ΔABC và ΔHAC có:
Suy ra: ΔABC đồng dạng với ΔHAC ( g.g)
Chọn đáp án A
Câu 8:
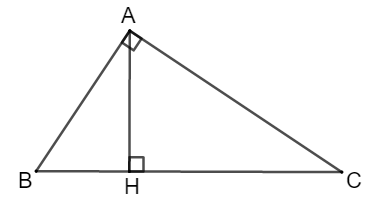
Cho tam giác ABC vuông tại A, kẻ AH vuông góc với BC. Biết BC = 20cm, AC = 12cm. Tính BH?
 Xem đáp án
Xem đáp án
Áp dụng định lí Pytago vào tam giác ABC ta có:
suy ra:
Nên AB = 16cm
* Xét tam giác AHB và tam giác CAB có:
Suy ra: Δ AHB và CAB đồng dạng ( g.g) .
Chọn đáp án D
Câu 9:
Cho tam giác ABC vuông tại A, kẻ đường cao AH. Biết AH = 6cm, BH = 3cm. Tính AC?
 Xem đáp án
Xem đáp án
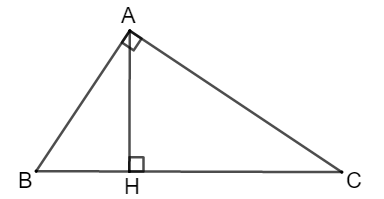

Chọn đáp án C
Câu 10:
Cho tam giác ABC có AB = 3cm, AC = 4cm, BC = 5cm. Tam giác MNP đồng dạng với tam giác ABC và diện tích tam giác MNP là . Tính độ dài các cạnh của tam giác MNP?
 Xem đáp án
Xem đáp án
Suy ra: tam giác ABC vuông tại A (định lý Py-ta-go đảo)
Diện tích tam giác ABC là:
*Gọi tam giác ABC đồng dạng với tam giác MNP theo tỉ số k
Suy ra:
Thay số
Chọn đáp án B
Câu 11:
Cho tam giác ABC vuông ở A, AB = 6cm, AC = 8cm, đường cao AH, đường phân giác BD. Tính độ dài các đoạn AD, DC lần lượt là
 Xem đáp án
Xem đáp án
+ Áp dụng định lý Pitago trong tam giác vuông ABC ta có:
+ Vì BD là đường phân giác của tam giác ABC nên áp dụng tính chất đường phân giác của tam giác, ta có:
=> AD = 3cm => DC = AC - AD = 8 - 3 = 5cm
Đáp án D.
Câu 12:
Cho tam giác ABC vuông ở A, AB = 6cm, AC = 8cm, đường cao AH, đường phân giác BD. Gọi I là giao điểm của AH và BD. Chọn kết luận đúng.
 Xem đáp án
Xem đáp án
+ Áp dụng định lý Pitago trong tam giác vuông ABC ta có:
+ Vì BD là đường phân giác của tam giác ABC nên áp dụng tính chất đường phân giác của tam giác, ta có:
=> AD = 3cm => DC = AC - AD = 8 - 3 = 5cm
Đáp án: B
Câu 13:
Cho tam giác ABC vuông ở A, AB = 6cm, AC = 8cm, đường cao AH, đường phân giác BD. Gọi I là giao điểm của AH và BD. Chọn khẳng định đúng.
 Xem đáp án
Xem đáp án
Xét 2 tam giác vuông ABD và HBI có:
(BD là tia phân giác của góc B)
=> ΔABD ~ ΔHBI (g - g)
AB.BI = BD.HB
Đáp án: A
Câu 14:
Cho tam giác ABC, phân giác AD. Gọi E, F lần lượt là hình chiếu của B và C lên AD. Chọn khẳng định đúng.
 Xem đáp án
Xem đáp án
Xét 2 tam giác vuông ABE và ACF ta có:
(vì AD là tia phân giác của góc A)
=> ΔABE ~ ΔACF (g - g)
(1)
Xét 2 tam giác vuông BDE và CDF ta có:
(2 góc đối đỉnh)
=> ΔBDE ~ ΔCDF (g - g)
(2)
Từ (1) và (2) ta có: AE.DF = AF.DE (đpcm)
Đáp án: C
Câu 15:
Cho tam giác ABC, phân giác AD. Gọi E, F lần lượt là hình chiếu của B và C lên AD. Chọn khẳng định không đúng.
 Xem đáp án
Xem đáp án
Xét 2 tam giác vuông ABE và ACF ta có:
(vì AD là tia phân giác của góc A)
=> ΔABE ~ ΔACF (g - g)
(1) => AE.CF = AF.BE hay A đúng
Xét 2 tam giác vuông BDE và CDF ta có:
(2 góc đối đỉnh)
=> ΔBDE ~ ΔCDF (g - g)
(2) hay D đúng
Từ (1) và (2) ta có: AE.DF = AF.DE hay C đúng
Đáp án: B
Câu 16:
Cho tam giác ABC vuông tại A, đường cao AH chia cạnh BC thành hai đoạn thẳng HB = 7cm và HC = 18cm. Điểm E thuộc đoạn thẳng HC sao cho đường thẳng đi qua E và vuông góc với BC chia tam giác ABC thành hai phần có diện tích bằng nhau. Tính CE.
 Xem đáp án
Xem đáp án
Gọi D là giao điểm của AC và đường vuông góc với BC tại E.
Xét ΔAHC và ΔABC có C chung và nên ΔAHC ~ ΔBAC (g-g)
Ta có (1), (2).
Từ (1) và (2) suy ra
Vì DE // AH (cùng vuông với BC) suy ra ΔDEC ~ ΔAHC nên
(4)
Từ (3) và (4) suy ra tức là => EC = 15cm.
Đáp án: A
Câu 17:
Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 3,5cm và HC = 9cm. Điểm E thuộc đoạn thẳng HC sao cho đường thẳng đi qua E và vuông góc với BC chia tam giác ABC thành hai phần có diện tích bằng nhau. Tính CE.
 Xem đáp án
Xem đáp án
Gọi D là giao điểm của AC và đường vuông góc với BC tại E.
Xét ΔAHC và ΔABC có C chung và nên ΔAHC ~ ΔBAC (g-g)
Ta có (1),
Từ (1) và (2) suy ra
Vì DE // AH (cùng vuông với BC) duy ra ΔDEC ~ ΔAHC nên
Từ (3) và (4) suy ra tức là => EC = 7,5cm.
Đáp án: D