Trắc nghiệm chuyên đề Toán 8 Chủ đề 3: Hình lăng trụ đứng. Diện tích xung quanh, thể tích của hình lăng trụ đung có đáp án
Trắc nghiệm chuyên đề Toán 8 Chủ đề 3: Hình lăng trụ đứng. Diện tích xung quanh, thể tích của hình lăng trụ đung có đáp án
-
402 lượt thi
-
9 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác đều, AB = 4cm,AA' = 5cm. Tính diện tích xung quanh, diện tích toàn phần và thể tích của hình lặng trụ AB C.A'B'C' ?
Xem đáp án
Xét tam giác ABC có nửa chu vi của tam giác là:
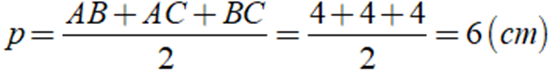
Khi đó ta có
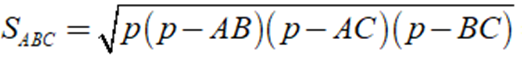
+ Diện tích xung quanh của hình lăng trụ Sxq = 2p.AA' = 2.6.5 = 60( cm2 )
+ Diện tích toàn phần của hình lăng trụ là Stp = Sxq + 2SABC = 60 + 2.4√ 3 = 60 + 8√ 3 ( cm2 )
+ Thể tích của hình lăng trụ là V = S.AA' = 4√ 3 .5 = 20√ 3 ( cm^3 ).
Câu 2:
Tính chiều cao của hình lăng trụ đứng ABCD.EFGH, biết rằng đáy ABCD là hình thoi có các đường chéo AC = 10cm,BD = 24cm và diện tích toàn phân bằng 1280cm2
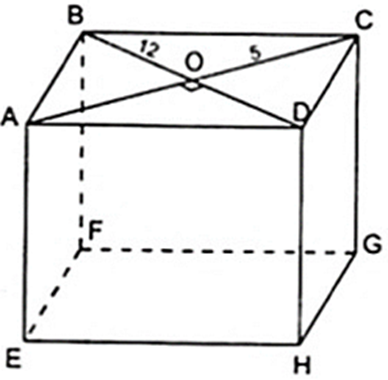
Xem đáp án
Áp dụng công thức: Stp = Sxq + 2Sd
Hay Sxq = Stp - 2Sd = 1280 - 2.1/2.1024
= 1280 - 240 = 1040( cm2 )
Vì đáy ABCD là hình thoi nên AC vuông góc với BD tại O (tính chất về đường chéo của hình thoi)
Áp dụng định lý Py – ta – go vào tam giác BOC vuông tại O ta được:
BC2 = BO2 + OC2 ⇒ BC2 = 122 + 52 = 132 ⇔ BC = 13( cm )
Chu vi đáy là 2p = 4.13 = 52( cm )
Áp dụng công thức Sxq = 2p.h
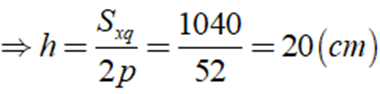
Câu 3:
Một trại hè có dạng hình lăng trụ đứng đáy tam giác, thể tích hình không gian bên trong là 2,16( cm3 ). Biết chiều dài lều AD = 2,4( cm ), chiều rộng của lều là 1,2cm. Tính chiều cao AH của lều?
Xem đáp án
Áp dụng công thức thể tích của hình lăng trụ đứng ta có: V = S.h
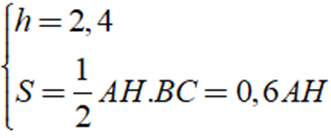
Do đó: V = S.h = 0,6AH.2,4 = 1,44AH
Theo giả thiết ta có: 1,44AH = 2,16 ⇔ AH = 1,5( cm )
Câu 4:
Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác ABC vuông tại A có AB = 3cm, AC = 4cm. Hình lăng trụ có chiều cao h = 3cm. Thể tích của hình lăng trụ đó là?
Xem đáp án
Ta có: SABC = 1/2AB.AC = 1/2.3.4 = 6( cm2 )
Khi đó: V = h.SABC = 3.6 = 18( cm3 )
Chọn đáp án B.
Câu 5:
Cho hình lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là hình chữ nhật, AB = 4cm BC = 5cm, chiều cao h = 2,5cm. Diện tích xung quanh của hình lăng trụ đứng là?
Xem đáp án
Ta có chu vi của đáy là: p = 2( AB + BC ) = 2( 4 + 5 ) = 18( cm )
Khi đó: Sxq = p.h = 18.2,5 = 45( cm2 )
Chọn đáp án B.
Câu 6:
Cho hình lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là hình chữ nhật, AB = 4cm BC = 5cm, chiều cao h = 2,5cm. Diện tích toàn phần của hình lăng trụ đứng là?
Xem đáp án
Theo câu 2, ta có: Sxq = 45( cm2 )
Khi đó ta có: Stp = Sxq + 2S = 45 + 2.4.5 = 85( cm2 )
Chọn đáp án B.
Câu 7:
Chọn phát biểu đúng trong các phát biểu sau:
Xem đáp án
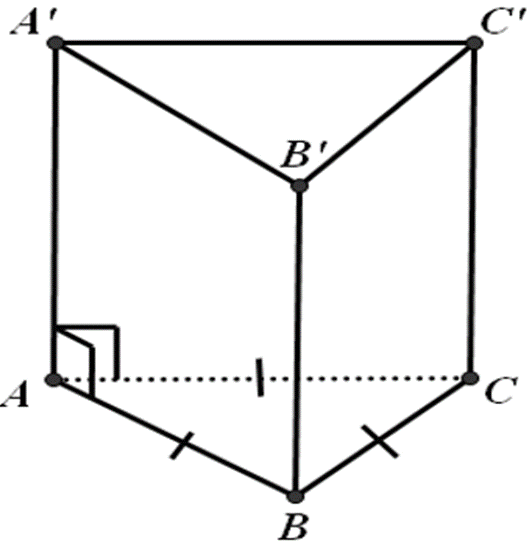
Hình lăng trụ tam giác gồm 5 mặt và 6 đỉnh.
+ 5 mặt:
( A'B'C' ), ( BCC'B' ), ( ABC ), ( A'C'CA ), ( ABB'A' )
+ 6 đỉnh là: A,B,C,A',B',C'
Chọn đáp án B.
Câu 8:
Tính chiều cao của hình lăng trụ đứng ABCD.EFGH, biết rằng đáy ABCD là hình thoi có các đường chéo AC = 10cm,BD = 24cm và diện tích toàn phân bằng 1280cm2
Xem đáp án
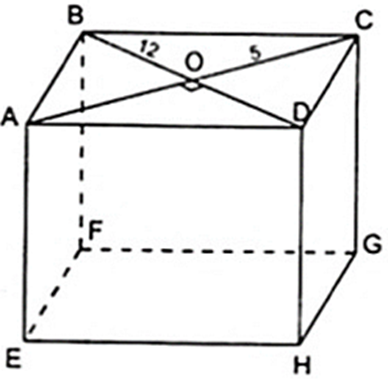
Áp dụng công thức: Stp = Sxq + 2Sd
Hay Sxq = Stp - 2Sd = 1280 - 2.1/2.1024
= 1280 - 240 = 1040( cm2 )
Vì đáy ABCD là hình thoi nên AC vuông góc với BD tại O (tính chất về đường chéo của hình thoi)
Áp dụng định lý Py – ta – go vào tam giác BOC vuông tại O ta được:
BC2 = BO2 + OC2 ⇒ BC2 = 122 + 52 = 132 ⇔ BC = 13( cm )
Chu vi đáy là 2p = 4.13 = 52( cm )
Áp dụng công thức Sxq = 2p.h
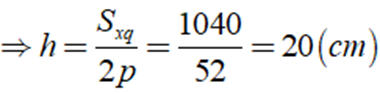
Câu 9:
Một trại hè có dạng hình lăng trụ đứng đáy tam giác, thể tích hình không gian bên trong là 2,16( cm3 ). Biết chiều dài lều AD = 2,4( cm ), chiều rộng của lều là 1,2cm. Tính chiều cao AH của lều?
Xem đáp án
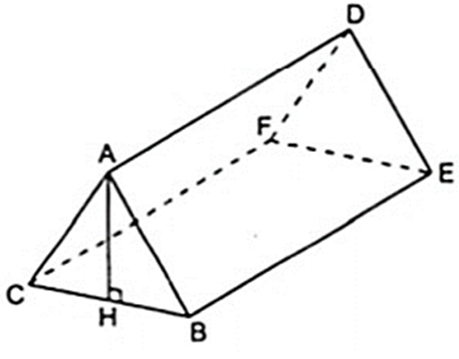
Áp dụng công thức thể tích của hình lăng trụ đứng ta có: V = S.h
Ta có:
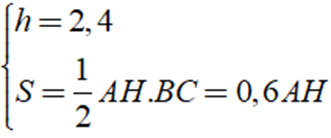
Do đó: V = S.h = 0,6AH.2,4 = 1,44AH
Theo giả thiết ta có: 1,44AH = 2,16 ⇔ AH = 1,5( cm )