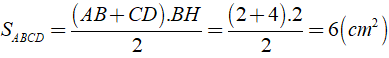Trắc nghiệm chuyên đề Toán 8 Chủ đề 4. Diện tích hình thang có đáp án
-
309 lượt thi
-
6 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Xem đáp án
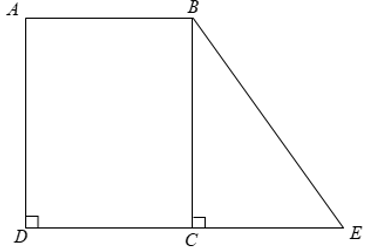
Theo bài ra ta có SABCD = AB.BC = 23.BC = 828 ⇒ BC = 36 ( cm )
Khi đó ta có
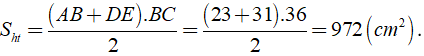
Câu 2:
Xem đáp án
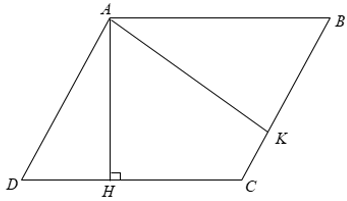
Xét hình bình bình ABCD có AB = CD = 8( cm ) và AD = BC = 6( cm )
Từ A kẻ các đường cao AH,AK.
Khi đó ta có:
+ Shbh = AH.CD = 8.AH
+ Shbh = AK.BC = 6.AK
Mà một hình bình hành thì chỉ có một diện tích chung nên 8.AH = 6.AK
Nếu độ dài đường cao thứ nhất là AH = 5( cm ) thì:
8.5 = 6.AK ⇔ AK = ( cm ) là độ dài đường cao thứ hai.
Nếu độ dài đường cao thứ nhất là AK = 5( cm ) thì:
8.AH = 6.5 ⇔ AH = ( cm ) là độ dài đường cao thứ hai.
Vậy bài toán này có hai đáp sốCâu 3:
Xem đáp án
Chọn đáp án B.
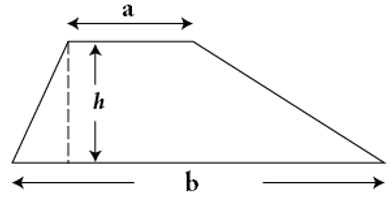
Ta có: S = ( a + b ).h
Khi đó ta có:
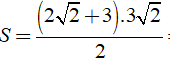
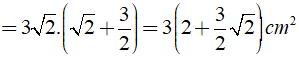
Câu 4:
Xem đáp án
Chọn đáp án A.
Diện tích của hình thang là S = ( a + b ).h
⇒ ( a + b ).h = 2S ⇔ h =
Khi đó, chiều cao của hình thang là h = = 3( cm ).
Câu 5:
Xem đáp án
Chọn đáp án B.
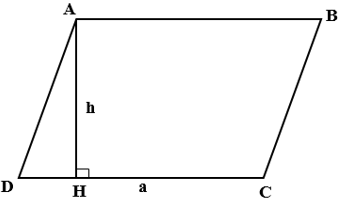
Ta có : S = a.h
Khi đó ta có: S = 4.2 = 8( cm2 ).
Câu 6:
Cho hình thang vuông ABCD ( Aˆ = Dˆ = 900 ), trong đó có Cˆ = 450, AB = 2cm, CD = 4cm. Diện tích của hình thang vuông ABCD là
Xem đáp án
Chọn đáp án D.
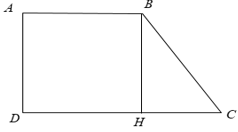
Xét hình thang ABCD
Từ B kẻ BH ⊥ CD, khi đó ta được hình chữ nhật ABHD ⇒ AB = DH = 2cm
⇒ HC = CD - DH = 4 - 2 = 2cm.
+ Xét Δ BDC có BH là đường cao đồng thời là đường trung tuyến
⇒ Δ BDC là tam giác cân tại B.
Mà BCDˆ = 450 ⇒ BDCˆ = 450
⇒ DBCˆ = 1800 - ( BCDˆ + BDCˆ ) = 1800 - 900 = 900.
⇒ Δ BDC là tam giác vuông cân tại B nên BH = DC = 2cm.
Do đó 