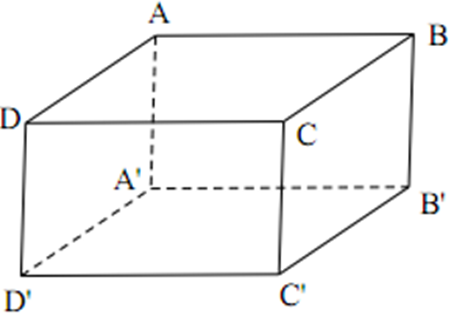
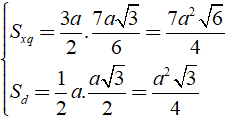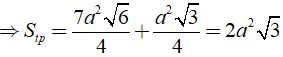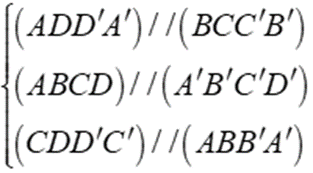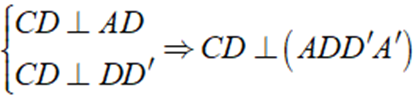Trắc nghiệm chuyên đề Toán 8 Chủ đề 6: Ôn tập và kiểm tra có đáp án
-
411 lượt thi
-
39 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Số mặt, số đỉnh, số cạnh của hình lập phương là?
Xem đáp án
Hình lập phương cũng được gọi là hình hộp chữ nhật có 6 mặt, 8 đỉnh, 12 cạnh.
Chọn đáp án B.
Câu 2:
Hình hộp chữ nhật có số cặp mặt song song là?
Xem đáp án
Hình hộp chữ nhật có 3 cặp mặt song song.
Chọn đáp án B.
Câu 4:
Cho hình hộp chữ nhật ABCD.A'B'C'D'. Chọn phát biểu đúng?
Xem đáp án
Ta có: ABCD là mặt đáy hình chữ nhật
⇒ AB//CD
Chọn đáp án A.
Câu 7:
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 2cm, AD = 3cm, AA' = 4cm. Thể tích hình hộp chữ nhật ABCD.A'B'C'D' ?
Xem đáp án
Ta có:
V = AB.AD.AA' = 2.3.4 = 24( cm3 )
Chọn đáp án B.
Câu 8:
Cho hình lập phương có các cạnh có độ dài là 5cm. Thể tích của hình lập phương đó là?
Xem đáp án
Thể tích hình lập phương cần tìm là:
V = a3 = 53 = 125( cm3 )
Chọn đáp án D.
Câu 9:
Cho hình hộp chữ nhật ABCD.A'B'C'D' có diện tích đáy SABCD = 24cm2 và có thể tích V = 84( cm3 ). Chiều cao của hình hộp chữ nhật có độ dài là?
Xem đáp án
Ta có: Thể tích cua hình hộp chữ nhật là: V = h.SABCD
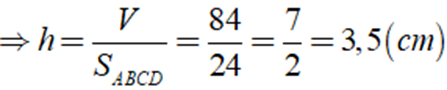
Vậy chiều cao của hình hộp chữ nhật là h = 3,5( cm )
Chọn đáp án B.
Câu 10:
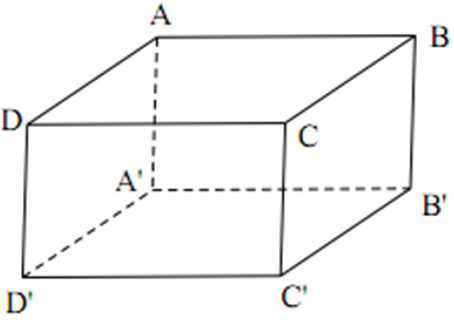
Cho hình hộp chữ nhật ABCD.A'B'C'D'. Chọn phát biểu đúng trong các phát biểu sau:
Xem đáp án
Ta có:
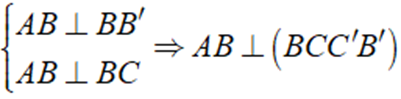
Mà AB ∈ ( ABB'A' ) ⇒ ( ABB'A' ) ⊥ ( BCC'B' )
Chọn đáp án C.
Câu 11:
Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác ABC vuông tại A có AB = 3cm, AC = 4cm. Hình lăng trụ có chiều cao h = 3cm. Thể tích của hình lăng trụ đó là?
Xem đáp án
Ta có: SABC = 1/2AB.AC = 1/2.3.4 = 6( cm2 )
Khi đó: V = h.SABC = 3.6 = 18( cm3 )
Chọn đáp án B.
Câu 12:
Cho hình lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là hình chữ nhật, AB = 4cm, BC = 5cm, chiều cao h = 2,5cm. Diện tích xung quanh của hình lăng trụ đứng là?
Xem đáp án
Ta có chu vi của đáy là: p = 2( AB + BC ) = 2( 4 + 5 ) = 18( cm )
Khi đó: Sxq = p.h = 18.2,5 = 45( cm2 )
Chọn đáp án B.
Câu 13:
Cho hình lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là hình chữ nhật, AB = 4cm, BC = 5cm, chiều cao h = 2,5cm. Diện tích toàn phần của hình lăng trụ đứng là?
Xem đáp án
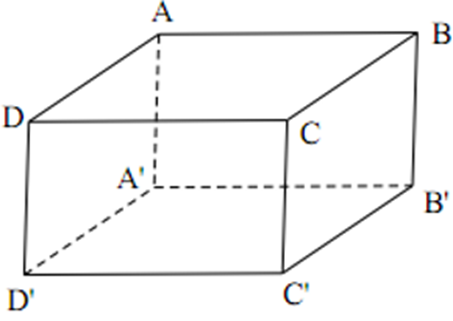
Theo câu 2, ta có: Sxq = 45( cm2 )
Khi đó ta có: Stp = Sxq + 2S = 45 + 2.4.5 = 85( cm2 )
Chọn đáp án B.
Câu 14:
Chọn phát biểu đúng trong các phát biểu sau:
Xem đáp án
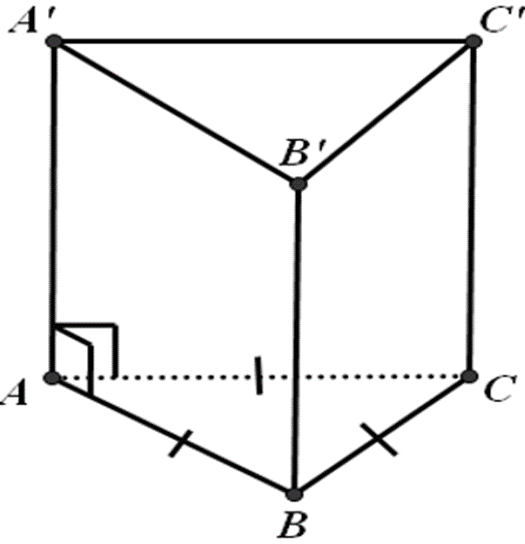
Hình lăng trụ tam giác gồm 5 mặt và 6 đỉnh.
+ 5 mặt:
( A'B'C' ), ( BCC'B' ), ( ABC ), ( A'C'CA ),( ABB'A' )
+ 6 đỉnh là: A,B,C,A',B',C'
Chọn đáp án B.
Câu 16:
Mặt bên của hình chóp cụt đều là hình gì?
Xem đáp án
Áp dụng định nghĩa của hình thang cân ta có: Mỗi mặt bên của hình chóp cụt đều là một hình thang cân.
Chọn đáp án C.
Câu 17:
Hình chóp tứ giác đều có mặt bên là hình gì?
Xem đáp án
Hình chóp tứ giác đều có mặt bên là tam giác cân.
Chọn đáp án A.
Câu 18:
Hình chóp lục giác đều có bao nhiêu mặt?
Xem đáp án
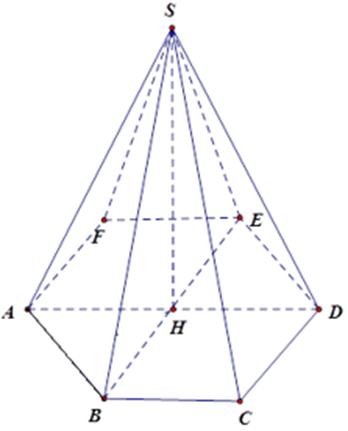
Hình chóp lục giác đều gồm có 6 mặt bên và 1 mặt đáy.
Chọn đáp án D.
Câu 19:
Các mặt bên của hình lăng trụ đứng là hình gì?
Xem đáp án
Hình lăng trụ đứng là hình có 2 mặt đáy là các đa giác, các mặt bên là hình chữ nhật
Chọn đáp án C.
Câu 20:
Các mặt bên của hình lăng trụ đứng?
Xem đáp án
Các mặt bên của hình lăng trụ đứng thì luôn song song với nhau, vuông góc với 2 mặt đáy và bằng nhau.
Chọn đáp án D.
Câu 21:
Cho hình lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là hình thang vuông ( Aˆ = Dˆ = 900 ). Có bao nhiêu cạnh song song với mặt phẳng ( BCC'B' ) ?
Xem đáp án
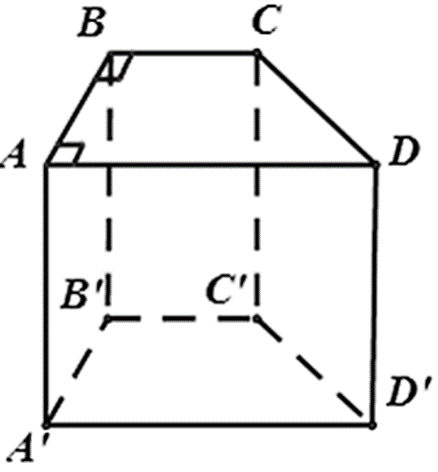
Vì
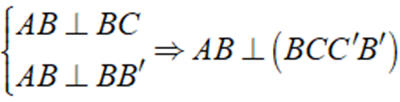
Tương tự: A'B' ⊥ ( BCC'B' ) ⇒ AB,A'B' ⊥ ( BCC'B' )
Chọn đáp án A.
Câu 22:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 3cm, chiều cao của hình chóp là h = 2cm. Thể tích của hình chóp đã cho là?
Xem đáp án
Áp dụng công thức thể tích của hình chóp ta có:
V = 1/3h.SABCD = 1/3.2.32 = 6( cm3 )
Chọn đáp án A.
Câu 23:
Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD có AB = 4cm,BC = 5cm. Biết thể tích của hình chóp S.ABCD bằng 36( cm3 ). Tính độ dài đường cao của hình chóp?
Xem đáp án
Áp dụng công thức thể tích của hình chóp ta có: V = 1/3.h.SABCD
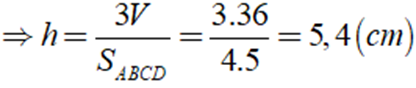
Chọn đáp án C.
Câu 24:
Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông cạnh bằng 4cm, các mặt bên là tam giác cân có độ dài cạnh bên là 6cm. Diện tích xung quanh của hình chóp đã cho là?
Xem đáp án
Chu vi của đáy ABCD là: 2( 4 + 4 ) = 16( cm )
Gọi d là độ dài trung đoạn của hình chóp
Ta có: d = √(62 - 22) = 4√2 ( cm )
Áp dụng công thức diên tích xung quanh của hình chóp: Sxq = p.d
⇒ Sxq = 8.4√2 = 32√2 ( cm2 )
Chọn đáp án B.
Câu 25:
Cho hình lăng trụ đứng ABC.A'B'C' có AB = 5cm, AC = 12cm,BC = 13cm. Có bao nhiêu mặt phẳng vuông góc với mặt phẳng ( ABB'A' ) ?
Xem đáp án
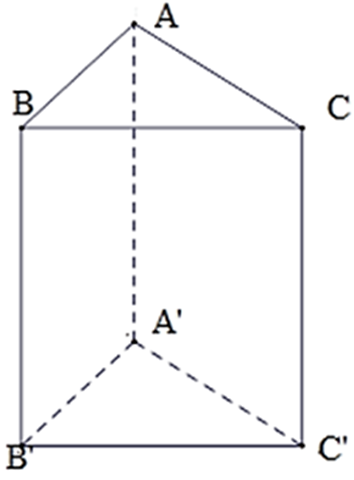
Ta có: AB2 + AC2 = BC2
⇒ Δ ABC vuông tại A.
Do đó:
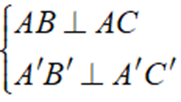
Vì AC vuông góc với hai đường thẳng cắt nhau là AB và AA'
Nên AC ⊥ ( ABB'A' )
Vậy có 3 mặt phẳng vuông góc với ( ABB'A' ) là:
( ABC ), ( A'B'C' ),( ACC'A' )
Chọn đáp án D.
Câu 26:
Cho hình lăng trụ đứng ABC.A'B'C' có BACˆ = 900 ,AB = 6cm, AC = 8cm, AA' = 15cm. Diện tích toàn phần của hình lăng trụ đó?
Xem đáp án
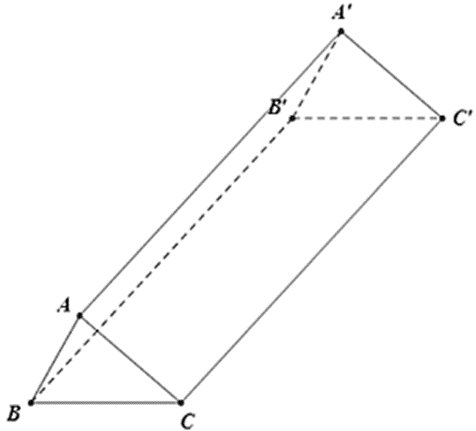
Ta có tam giác ABC vuông tại A
BC2 = AB2 + AC2 ⇒ BC = 10cm
Chu vi của đáy là: 24cm
Khi đó: Sxq = 24.15 = 360( cm2 )
+ Stp = Sxq + 2Sd = 360 + 2.1/2.6.8 = 408( cm2 )
Chọn đáp án D.
Câu 27:
Cho hình hộp chữ nhật có diện tích xung quanh bằng tổng diện tích hai đáy, chiều cao bằng 6cm. Một kích thức của đáy bằng 10cm. tính kích thước còn lại?
Xem đáp án
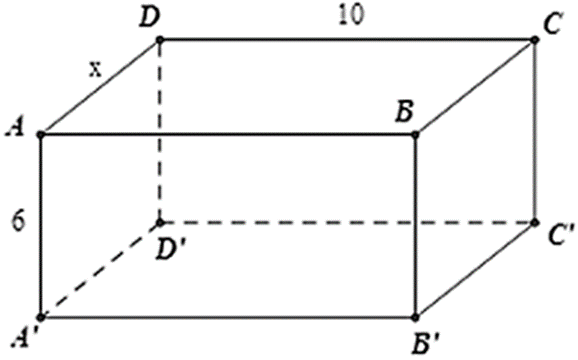
Chu vi của đáy bằng: 2( x + 10 )
Diện tích xung quanh: Sxq = 2( x + 10 ).6 = 12( x + 10 )
Diện tích đáy: 10x
Theo giả thiết ta có: 12( x + 10 ) = 20x ⇔ x = 15
Chọn đáp án A.
Câu 28:
Cho hình lăng trụ tam giác đều ABC.A'B'C' có chiều cao bằng 2cm, BAB'ˆ = 450 . Tính diện tích xung quanh của hình lăng trụ?
Xem đáp án
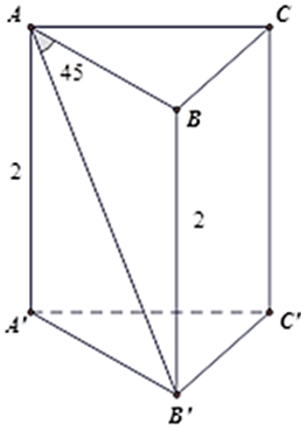
Tam giác vuông ABB' có BAB'ˆ = 450 nên là tam giác vuông cân tại B nên AB = BB' = 2cm.
Vì ABC là tam giác đều nên chu vi đáy bằng 6( cm )
Khi đó diện tích xung quanh hình lăng trụ là Sxq = 6.2 = 12( cm2 )
Chọn đáp án C.
Câu 29:
Cho hình lăng trụ tam giác đều ABC.A'B'C' có chiều cao bằng 2cm, BAB'ˆ = 450 . Tính diện tích toàn phần của hình lăng trụ?
Xem đáp án
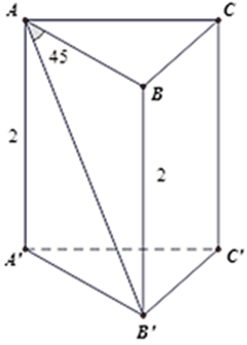
Tam giác vuông ABB' có BAB'ˆ = 450 nên là tam giác vuông cân tại B nên AB = BB' = 2cm.
Vì ABC là tam giác đều nên chu vi đáy bằng 6( cm )
Khi đó diện tích xung quanh hình lăng trụ là Sxq = 6.2 = 12( cm2 )
Diện tích toàn phần là Stp = Sxq + 2Sd = 12 + 2.1/2.2.2.sin 600 = 12 + 2√3 ( cm2 )
Chọn đáp án B.
Câu 30:
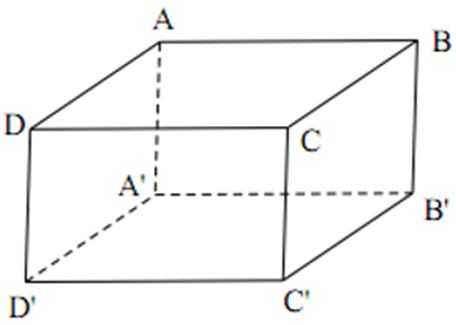
Cho hình hộp chữ nhật ABCD.A'B'C'D'
a) Nếu O là trung điểm của đoạn CB1 thì O có là điểm thuộc đoạn BC1 ?
b) K là điểm thuộc cạnh CD, liệu K có thể là điểm thuộc cạnh BB1 hay không?
Xem đáp án
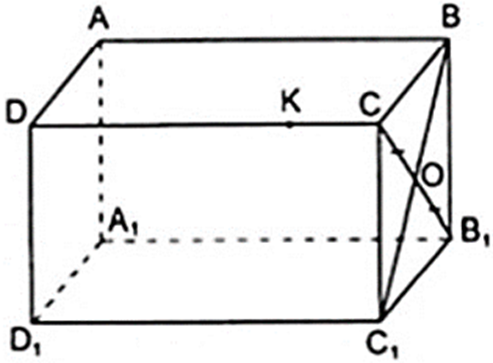
a) Câu trả lời trên là có. Thật vậy, vì mặt bên BCC1B1 là hình chữ nhật có O là trung điểm của đường chéo CB1 nên O cũng là trung điểm của đường chéo BC1 (theo tính chất đường chéo của hình chữ nhật). Vậy thuộc đoạn BC1.
b) K không thuộc cạnh BB1 vì K ∉ mp( BB1C1C ) mà BB1 thuộc mặt phẳng đó
Vậy K không thuộc cạnh BB1.
Câu 31:
Các kích thước của hình hộp chữ nhật ABCD.A1B1C1D1 là DC = 5 cm; CB = 4cm; BB1 = 3 cm. Tính các độ dài DC1, CB1 ?
Xem đáp án
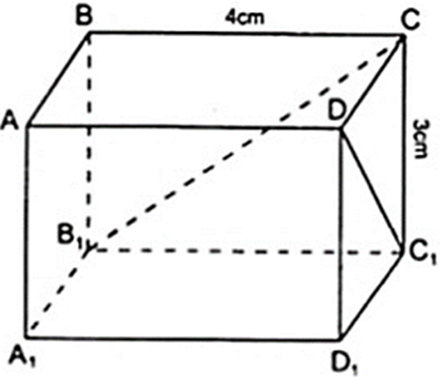
DC1 ∈ mp( DCC1D1 ) là hình chữ nhật nên Δ DCC1 vuông tại C.
Áp dụng định lý Py – ta – go vào Δ DCC1 vuông tại C ta được: DC12 = CC12 + CD2
Hay DC12 = 32 + 52 ⇔ DC12 = ( √34 )2 ⇔ DC1 = √34 ( cm )
CB1 ∈ ( BCC1B1 ) là hình chữ nhật nên Δ BCB1 vuông tại B.
Áp dụng định lí Py – ta – go vào Δ BCB1 vuông tại B ta được: CB12 = CB2 + BB12
Hay CB12 = 32 + 42 = 52 ⇔ CB1 = 5( cm )
Vậy DC1 = √34 ( cm ); CB1 = 5( cm )
Câu 32:
Xét sự đúng sai trong các phát biểu sau?
a) Hình chóp đều có đáy là hình thoi và chân đường cao trùng với giao điểm hai đường chéo của đáy.
b) Hình chóp đều có đáy là hình chữ nhật và chân đường cao trùng với giao điểm hai đường chéo của đáy.
Xem đáp án
a) Sai, vì hình thoi không phải là tứ giác đều (các góc không bằng nhau).
b) Sai, vì hình chữ nhật không phải là tứ giác đều (các cạnh không bằng nhau).
Câu 33:
Cho hình hộp chữ nhật ABCD.A1B1C1D1 có ABCD là hình vuông. Gọi O là giao điểm của AC và BD, O1 là giao điểm của A1C1 và B1D1. Chứng minh rằng:
a) BDD1B1 là hình chữ nhật.
b) OO1 ⊥ ( ABCD )
Xem đáp án
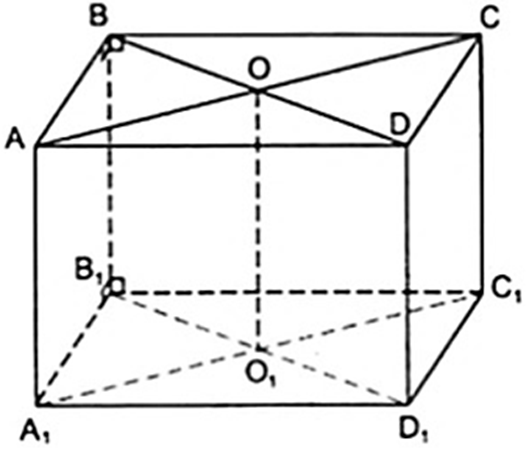
a) Từ giả thiết ABCD.A1B1C1D1 là hình hộp chữ nhật nên các mặt bên ( BB1A1A ),( BB1C1C ) là hình chữ nhật, do đó ta có:
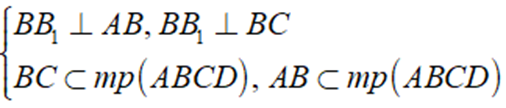
⇒ BB1 ⊥ mp( ABCD )
Mặt khác đường chéo BD ⊂ mp( ABCD ) và đi qua B nên:
BB1 ⊥ BD ⇒ B1BDˆ = 900
Chứng minh tương tự như trên, ta cũng được: BB1D1ˆ = BDD1ˆ = 900
Điều đó chứng tỏ tứ giác BDD1B1 có ba góc vuông nên là hình chữ nhật.
b) Chứng minh tương tự như câu a, ta có tứ giác ACC1A1 là hình chữ nhật
Áp dụng tính chất đường chéo và các hình vuông ABCD, A1B1C1D1 ta được O là trung điểm của AC và BD và O1 là trung điểm của A1C1 và B1D1
⇒ OO1 là đường trung bình của các hình chữ nhật BDD1B1 và ACC1A1
Do đó: OO1//BB1//DD1//AA1//CC1
Suy ra
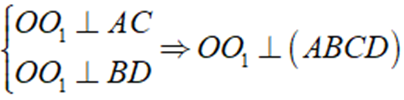
Câu 34:
Các kích thức của hình hộp chữ nhật như trên hình vẽ. Tính độ dài của đoạn AC1 ?
Xem đáp án
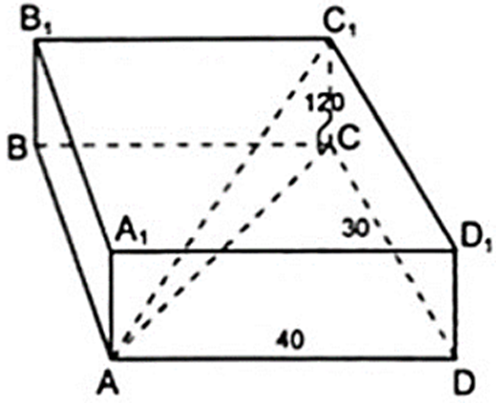
Vì ABCD.A1B1C1D1 là hình hộp chữ nên
CC1 ⊥ mp( ABCD ) ⇒ CC1 ⊥ AC hay tam giác ACC1 vuông tại C, đáy ABCD là hình chữ nhật nên tam giác ACD vuông tại D.
Áp dụng định lý Py – ta – go ta có:
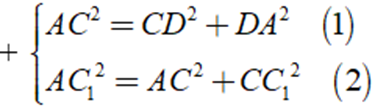
Thay đẳng thức ( 1 ) vào ( 2 ) ta được:
AC12 = CD2 + AD2 + CC12 ⇒ AC1 = √(CD2 + AD2 + CC12)
Hay AC1 = √(302 + 402 + 1202) = √(1302) = 130( cm )
Câu 35:
Tính chiều cao của hình lăng trụ đứng ABCD.EFGH, biết rằng đáy ABCD là hình thoi có các đường chéo AC = 10cm,BD = 24cm và diện tích toàn phân bằng 1280cm2
Xem đáp án
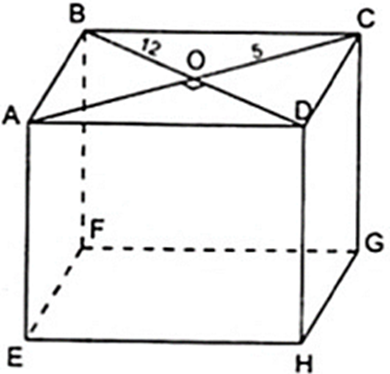
Áp dụng công thức: Stp = Sxq + 2Sd
Hay Sxq = Stp - 2Sd = 1280 - 2.1/2.1024
= 1280 - 240 = 1040( cm2 )
Vì đáy ABCD là hình thoi nên AC vuông góc với BD tại O (tính chất về đường chéo của hình thoi)
Áp dụng định lý Py – ta – go vào tam giác BOC vuông tại O ta được:
BC2 = BO2 + OC2 ⇒ BC2 = 122 + 52 = 132 ⇔ BC = 13( cm )
Chu vi đáy là 2p = 4.13 = 52( cm )
Áp dụng công thức Sxq = 2p.h ⇒ h = Sxq/(2p) = 1040/52 = 20( cm )
Câu 36:
Một trại hè có dạng hình lăng trụ đứng đáy tam giác, thể tích hình không gian bên trong là 2,16( cm3 ). Biết chiều dài lều AD = 2,4( cm ), chiều rộng của lều là 1,2cm. Tính chiều cao AH của lều?
Xem đáp án
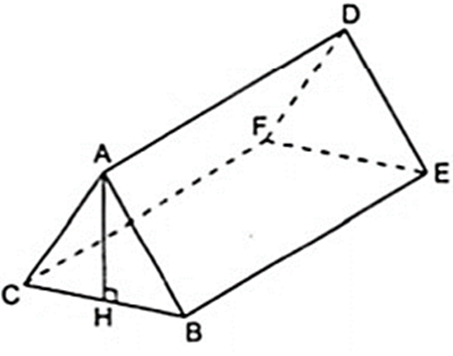
Áp dụng công thức thể tích của hình lăng trụ đứng ta có: V = S.h
Ta có:
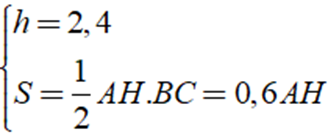
Do đó: V = S.h = 0,6AH.2,4 = 1,44AH
Theo giả thiết ta có: 1,44AH = 2,16 ⇔ AH = 1,5( cm )
Câu 37:
Cho hình hộp chữ nhật có diện tích xung quang 120cm2, chiều cao bằng 6cm. Tìm các kích thước của đáy để hình hộp chữ nhật có thể tích lớn nhất?
Xem đáp án
Gọi a và b là các kích thước của đáy
Thể tích của hình hộp chữ nhật là V = 6ab
Để V lớn nhất ⇔ ab lớn nhất
Ta có: Sxq = 120 ⇒ 2( a + b ).6 = 120 ⇔ a + b = 10
+ ab = a( 10 - a ) = - a2 + 10a = - ( a - 5 )2 + 25 ≤ 25
Khi đó ta có: ⇒ V = 6ab ≤ 6.25 = 150
Thể tích lớn nhất bằng 150cm3 khi và chỉ khi a = b = 5cm.
Câu 38:
Cho hình lăng trụ đứng có đáy là hình thoi và các đường chéo là 16cm và 30 cm. Diện tích toàn phần của hình lăng trụ là 1840cm2. Tính chiều cao của hình lăng trụ
Xem đáp án
Hướng dẫn giải:
Độ dài cạnh của hình thoi là: a = √(82 + 152) = 17( cm )
Gọi h là độ dài đường cao của hình lăng trụ
Chu vi của hình thoi là 68( cm )
Diện tích xung quanh của hình thoi là: Sxq = 68.h
Diện tích toàn phần là Stp = Sxq + 2Sd = 68h + 1/2.2.16.30 = 68h + 480
Theo giả thiết ta có: Stp = 1840 ⇒ 68h + 480 = 1840 ⇔ h = 20( cm )
Câu 39:
: Tính diện tích toàn phần của hình chóp tam giác đều có cạnh đáy bằng a và chiều cao bằng 2a.
Xem đáp án
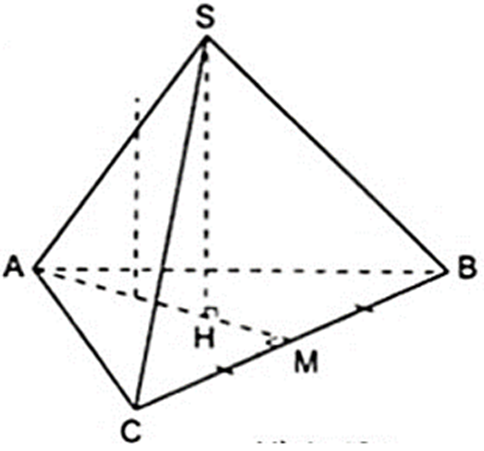
Xét hình chóp S.ABC có AB = AC = BC = a và SH = 2a.
Gọi M là trung điểm của BC thì AM vừa là đường trung tuyến, vừa là đường cao, vừa là đường phân giác của tam giác đều ABC nên AM ⊥ BC và HM = 1/3AM.
Áp dụng định lý Py – ta – go vào tam giác vuông ABM vuông tại M ta được:
AB2 = BM2 + AM2 ⇒ a2 = ( a/2 )2 + AM2
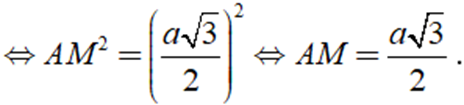
Do đó HM = (a√3 )/6.
Áp dụng định lí Py – ta – go vào tam giác vuông SHM vuông tại H, ta có:
SM2 = HM2 + SH2
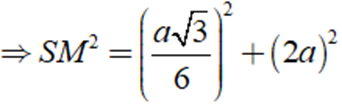
Áp dụng công thức: Stp = Sxq + Sd
Ta có:
