Trắc nghiệm chuyên đề Toán 8 Chủ đề 8: Hình chữ nhật có đáp án
-
450 lượt thi
-
8 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Cho tam giác ABC, đường cao AH. Gọi I là trung điểm của AC, E là điểm đối xứng với H qua I. Chứng minh tứ giác AHCE là hình chữ nhật.
Xem đáp án
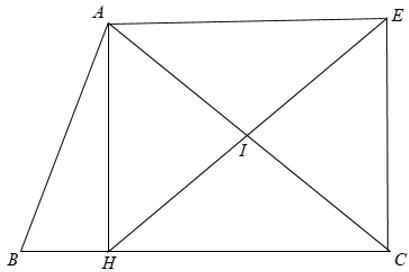
+ Trong Δ AHC vuông có I là trung điểm của AC
⇒ HE là đường trung tuyến của Δ AHC.
⇒ HI = AC = AI = IC.
Mà E đối xứng với H qua I ⇒ HI = IE.
Khi đó ta có HI = IE = AI = IC.
+ Xét Δ HCE có CI là đường trung tuyến ứng với cạnh HE
mà CI = HE ⇒ Δ HCE vuông tại C.
Tương tự xét với Δ AHE,Δ AEC đều là các tam giác vuông tại A, E.
Xét tứ giác AHCE có = 900
⇒ AHCE là hình chữ nhật.Câu 2:
Tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì ? Giải thích ?
Xem đáp án
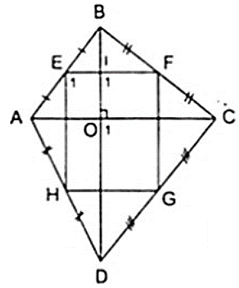
Tứ giác EFGH là hình chữ nhật.
Giải thích: Theo giả thiết ta có EF, GH lần lượt là đường trung bình của tam giác Δ ABC,Δ ADC
Áp dụng định lí đường trung bình vào hai tam giác ta được
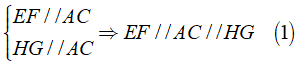
Chứng minh tương tự: EH//FG//BD ( 2 )
Từ ( 1 ) và ( 2 ), tứ giác EFGH có hai cặp cạnh đối song song nên tứ giác EFGH là hình bình hành.
Gọi O là giao điểm của AC và BD, I là giao điểm của EF với BD.
Áp dụng tính chất của các góc đồng vị vào các đường thẳng song song ở trên và giả thiết nên ta có:
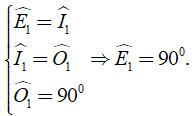
Hình bình hành EFGH có một góc vuông nên EFGH là hình chữ nhật.
Câu 3:
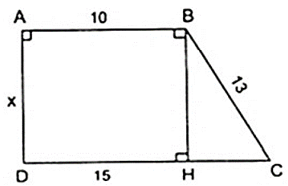
Tìm giá trị của x từ các thông tin trên hình sau ?
Xem đáp án
Kẻ BH ⊥ CD, tứ giác ABHD có = 900
⇒ Tứ giác ABHD là hình chữ nhật.
Áp dụng tính chất của hình chữ nhật ta có:
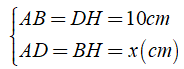
Ta có: CD = DH + HC ⇒ HC = CD - DH = 15 - 10 = 5( cm )
+ Xét Δ BCH, áp dụng định lý Py – to – go ta có:
BC2 = HC2 + BH2 ⇒ BH2 = BC2 - HC2
⇒BH==12( cm )
Do đó BH = AD = x = 12( cm ). Vậy x = 12
Câu 4:
Xem đáp án
Định nghĩa: Hình chữ nhật là tứ giác có bốn góc vuông.
Câu 5:
Xem đáp án
Định lý trong hình chữ nhật
+ Hình chữ nhật có hai đường chéo bằng nhau.
+ Hình chữ nhật có hai đường chéo cắt nhau tại trung điểm tại trung điểm mỗi đường.
+ Giao của hình đường chéo của hình chữ nhật là tâm của hình chữ nhật đó.
+ Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông
⇒ Đáp án C sai.
Câu 6:
Xem đáp án
Dấu hiệu nhận biết hình chữ nhật:
+ Tứ giác có ba góc vuông là hình chữ nhật.
+ Hình thang cân có một góc vuông là hình chữ nhật.
+ Hình bình hành có một góc vuông là hình chữ nhật.
+ Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.
⇒ Hình bình hành có hai đường chéo cắt nhau tại trung điểm mỗi đường chưa đủ điều kiện để là hình chữ nhật.
Câu 7:
Xem đáp án
Định lý
+ Trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.một cạnh bằng nửa cạnh ấy thì tam giác đó là tam giác vuông.
+ Nếu một tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh ấy thì tam giác đó là tam giác vuông.
⇒ Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền thì vuông góc với cạnh huyền nếu tam giác vuông đó là tam giác vuông cân.
Câu 8:
Xem đáp án
Độ dài của đường chéo hình chữ nhật bằng căn bậc hai tổng hai bình phương của hai kích thước hình chữ nhật
Do đó, độ dài đường chéo là = 13( cm )