27 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 8 Bài tập Ôn tập chương 4 (Có đáp án)

Câu 1:

Cho các bất phương trình sau, đâu là bất phương trình bậc nhất một ẩn?

A. 5x + 7 < 0

B. 0x + 6 > 0

C. x² – 2x > 0

D. x – 10 = 3

Xem đáp án

Dựa vào định nghĩa bất phương trình bậc nhất một ẩn ta có:

Đáp án A là bất phương trình bậc nhất một ẩn.

Đáp án B không phải bất phương trình bậc nhất một ẩn vì a = 0.

Đáp án C không phải bất phương trình bậc nhất một ẩn vì có x²

Đáp án D không phải bất phương trình vì đây là phương trình bậc nhất một ẩn.

Đáp án cần chọn là: A

Câu 2:

Giá trị x = 2 là nghiệm của bất phương trình nào sau đây?

A. 7 – x < 2x

B. 2x + 3 > 9

C. -4x ≥ x + 5

D. 5 – x > 6x – 12

Xem đáp án

(Trong bài này chúng ta làm theo cách thứ 2) thay x = 2 vào từng bất phương trình:

Đáp án A: 7 – 2 < 2.2 ó 5 < 4 vô lý. Loại đáp án A.

Đáp án B: 2.2 + 3 > 9 ó 7 > 9 vô lý. Loại đáp án B

Đáp án C: -4.2 ≥ 2 + 5 ó -8 ≥ 7 vô lý. Loại đáp án C.

Đáp án D: 5 – 2 > 6.2 ó 3 > 0 luôn đúng. Chọn đáp án D

Đáp án cần chọn là: D

Câu 3:

Nghiệm của bất phương trình 7(3x + 5) >0 là:

A. x > $\frac{3}{5}$

B. x ≤ $- \frac{5}{3}$

C. x ≥ $- \frac{5}{3}$

D. x > $- \frac{5}{3}$

Xem đáp án

Vì 7 > 0 nên 7(3x + 5) ≥ 0 ó 3x + 5 > 0 ó 3x > -5 ó x > $- \frac{5}{3}$

Đáp án cần chọn là: D

Câu 4:

Cho a > b. Bất đẳng thức nào tương đương với bất đẳng thức đã cho?

A. a – 3 > b – 3

B. -3a + 4 > -3b + 4

C. 2a + 3 < 2b + 3

D. -5a – 1 < -5a – 1

Xem đáp án

+) Đáp án A: a > b ó a – 3 > b – 3

Vậy ý A đúng chọn luôn ý A

+) Đáp án B: -3a + 4 > -3b + 4 ó -3a > -3b ó a < b trái với giải thiết nên B sai

+) Đáp án C: 2a + 3 < 2b + 3 ó 2a < 2b ó a < b trái với giả thiết nên C sai.

+) Đáp án D: -5b – 1 < -5a – 1 ó -5a < -5a ó b > a trái với giả thiết nên D sai.

Đáp án cần chọn là: A

Câu 5:

Phương trình |2x – 5| = 1 có nghiệm là:

A. x = 3; x = 2

B. x = $\frac{5}{2}$ ; x = 2

C. x = 1; x = 2

D. x = 0,5; x = 1,5

Xem đáp án

Giải phương trình: |2x – 5| = 1

TH1: 2x – 5 ≥ 0 ó x ≥ $\frac{5}{2}$ => |2x – 5| = 2x – 5 = 1 ó 2x = 6 ó x = 3 (tm)

TH2: 2x – 5 < 0 ó x < $\frac{5}{2}$ => |2x – 5| = -2x + 5 = 1 ó 2x = 4 ó x = 2 (tm)

Vậy phương trình có hai nghiệm x = 3 và x = 2

Đáp án cần chọn là: A

Câu 6:

Phương trình $\frac{1}{3} - | \frac{5}{4} - 2 x | = \frac{1}{4}$ có nghiệm là

A. x = 1/12; x = 7/12

B. x = 8/12; x = 5/12

C. x = 7/12 ; x = 2/3

D. x = 1/12 ; x = 5/12

Xem đáp án

Câu 7:

Hình vẽ dưới đây là biểu diễn tập nghiệm của bất phương tình nào?

A. x – 1 ≥ 5

B. x + 1 ≤ 7

C. x + 3 < 9

D. x + 1 > 7

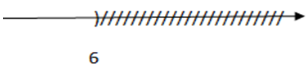
Xem đáp án

Theo đề bài thì trục số biểu diễn tập nghiệm x < 6

Ta có

+) Đáp án A: x – 1 ≥ 5 ó x ≥ 6 loại vì tập nghiệm là x < 6.

+) Đáp án B: x + 1 ≤ 7 ó x ≤ 6 loại vì tập nghiệm là x < 6.

+) Đáp án C: x + 3 < 9 ó x < 6 thỏa mãn vì tập nghiệm là x < 6.

+) Đáp án D: x + 1 > 7 ó x > 6 loại vì tập nghiệm là x < 6.

Đáp án cần chọn là: C

Câu 8:

Với giá trị nào của m thì bất phương trình m(2x + 1) < 8 là bất phương tình bậc nhất một ẩn?

A. m ≠ 1

B. m ≠ $- \frac{1}{3}$

C. m ≠ 0

D. m ≠ 8

Xem đáp án

Ta có m(2x + 1) < 8 ó 2mx + m < 8 ó 2mx + m – 8 < 0

Vậy để bất phương trình m(2x + 1) < 8 là bất phương trình bậc nhất 1 ẩn thì 2mx + m – 8 < 0 là bất phương trình bậc nhất một ẩn.

Theo định nghĩa bất phương trình bậc nhất một ẩn thì a ≠ 0 hay 2m ≠ 0 ó m ≠ 0

Đáp án cần chọn là: C

Câu 9:

Tập nghiệm của bất phương trình 3x + 7 > x + 9 là

A. S = {x|x > 1}

B. S = {x|x > -1}

C. x = 1

D. S = {x|x < 1}

Xem đáp án

3x + 7 > x + 9 ó 3x – x > 9 – 7 ó 2x > 2 ó x > 1

Vậy tập nghiệm của bất phương trình là S = {x|x > 1}

Đáp án cần chọn là: A

Câu 10:

Phương trình |5x – 4| = |x + 2| có nghiệm là

A. x = $\frac{1}{3}$

B. x = 1,5; x = $- \frac{1}{3}$

C. x = -1,5; x = $- \frac{1}{3}$

D. x = 1,5; x = $\frac{1}{3}$

Xem đáp án

Câu 11:

Tổng các nghiệm của phương trình 7,5 – 3|5 – 2x| = -4,5 là

A. 1/2

B. 9/2

C. 5

D. 11/2

Xem đáp án

Câu 12:

Số nghiệm của phương trình |2x – 3| - |3x + 2| = 0 là

A. 0

B. 1

C. 2

D. 5

Xem đáp án

Câu 13:

Nghiệm của phương trình |x – 1| = 3x – 2 là:

A. x = 3/4

B. x = 1/2; x = 3/4

C. x = 1

D. Phương trình vô nghiệm

Xem đáp án

Câu 14:

Hình vẽ nào dưới đây biểu diễn tập nghiệm của phương trình 2x – 8 ≤ 13 – 5x.

A.

B.

C.

D.

Xem đáp án

2x – 8 ≤ 13 – 5x ó 2x + 5x ≤ 13 + 8 ó 7x ≤ 21 ó x ≤ 21 : 7 ó x ≤ 3

Vậy tập nghiệm của phương trình S = {x|x ≤ 3}

Biểu diễn tập nghiệm trục số

Đáp án cần chọn là: C

Câu 15:

Số nguyên lớn nhất thỏa mãn bất phương trình (x – 2)² – x² – 8x + 3 ≥ 0 là

A. x = 1

B. x = 0

C. x = -1

D. x ≤ 7/12

Xem đáp án

(x – 2)² – x² – 8x + 3 ≥ 0

ó x² – 4x + 4 – x² – 8x + 3 ≥ 0

ó -12x + 7 ≥ 0

ó x ≤ 7/12

Vậy nghiệm của bất phương trình là x ≤ 7/12

Nên số nguyên lớn nhất thỏa mãn bất phương trình là x = 0

Đáp án cần chọn là: B

Câu 16:

Số nguyên nhỏ nhất thỏa mãn bất phương trình x(5x + 1) + 4(x + 3) > 5x² là

A. x = -3

B. x = 0

C. x = -1

D. x = -2

Xem đáp án

x(5x + 1) + 4(x + 3) > 5x²

ó 5x² + x + 4x + 12 > 5x²

ó 5x > -12

ó x > -12/5

Vậy nghiệm của bất phương trình là x > -12/5.

Số nguyên lớn nhất thỏa mãn bất phương trình là x = 02

Đáp án cần chọn là: D

Câu 17:

Bất phương trình $\frac{3 x + 5}{2} - 1 \leq \frac{x + 2}{3} + x$ có nghiệm là

A. Vô nghiệm

B. x ≥ 4,11

C. Vô số nghiệm

D. x ≤ -5

Xem đáp án

Câu 18:

Bất phương tình 2(x – 1) – x > 3(x – 1) – 2x – 5 có nghiệm là:

A. Vô số nghiệm

B. x < 3,24

C. x > 2,12

D. Vô nghiệm

Xem đáp án

Ta có: 2(x – 1) – x > 3(x – 1) – 2x – 5

ó 2x – 2 – x > 3x – 3 – 2x – 5

ó x – 2 > x – 8

ó -2 > -8 (luôn đúng)

Vậy bất phương trình trên có vô số nghiệm.

Đáp án cần chọn là: A

Câu 19:

Tập nghiệm của bất phương trình $\frac{x - 3}{x + 4} < 0$ là

A. x > 4

B. -4 < x < 3

C. x < 3

D. x ≠ -4

Xem đáp án

Câu 20:

Tìm giá trị của x để biểu thức A = $\frac{5 - 2 x}{x^{2} + 4}$ có giá trị dương

A. x < 5/2

B. x > 5/2

C. x = 5/2

D. x > 2

Xem đáp án

Câu 21:

Phương trình |x – 1| + |x - 3| = 2x – 1 có số nghiệm là

A. 2

B. 1

C. 3

D. 0

Xem đáp án

Đặt |x – 1| + |x - 3| = 2x – 1 (1)

Xét +) x – 1 = 0 ó x = 1

+) x – 3 = 0 ó x = 3

Ta có bảng xét dấu đa thức x – 1 và x – 3 dưới đây

x	1 3
x – 1	- 0 + \| +
x – 3	- \| - 0 +

+ Xét khoảng x < 1 ta có:

(1) ó (1 – x) + (3 – x) = 2x – 1 ó -2x + 4 = 2x – 1 ó 4x = 5 ó x = $\frac{5}{4}$

(Không thuộc khoảng đang xét)

(1) ó (x – 1) + (3 – x) = 2x – 1 ó 2 = 2x – 1 ó x = $\frac{3}{2}$ (TM)

+) Xét khoảng x > 3 ta có:

(1) ó (x – 1) + (x – 3) = 2x – 1 ó 0.x = -3 (phương trình vô nghiệm)

Vậy phương trình có nghiệm x = $\frac{3}{2}$

Đáp án cần chọn là: B

Câu 22:

Nghiệm của bất phương trình $\frac{x + 4}{x + 1} + \frac{x}{x - 1} < \frac{2 x^{2}}{x^{2} - 1}$ là

A. x < -1

B. x < 1

C. x > 1

D. x > -1

Xem đáp án

Câu 23:

Chọn câu đúng, biết 0 < a < b.

A. $\frac{a}{b} + \frac{b}{a} < 2$

B. $\frac{a}{b} + \frac{b}{a} > 2$

C. $\frac{a}{b} + \frac{b}{a} \geq 2$

D. $\frac{a}{b} + \frac{b}{a} = 1$

Xem đáp án

Câu 24:

Cho số thực x, chọn câu đúng nhất.

A. x⁴ + 3 ≥ 4x

B. x⁴ + 5 > x² + 4x

C. Cả A, B đều sai

D. Cả A, B đều đúng

Xem đáp án

+) Đáp án A: Bất đẳng thức tương đương với x⁴ – 4x + 3 ≥ 0

ó (x – 1)(x³ + x² + x – 3) ≥ 0

ó (x – 1)((x³ – 1) + (x² + x – 2)) ≥ 0

ó (x – 1)((x – 1)(x² + x + 1) + (x – 1)(x + 2)) ≥ 0

ó (x – 1)(x – 1)(x² + x + 1 + x + 2) ≥ 0

ó (x – 1)²(x² + 2x + 3) ≥ 0

ó (x – 1)²[(x + 1)² + 1] ≥ 0 (luôn đúng với mọi số thực x)

Đẳng thức xảy ra khi và chỉ khi x = 1.

Nên A đúng

+) Đáp án B: Bất đẳng thức tương đương với x⁴ – x² – 4x + 5 > 0

ó x⁴ – 2x² + 1 + x² – 4x + 4 > 0

ó (x² – 1)² + (x – 2)² > 0

Ta có: (x² – 1) ≥ 0, (x – 2)² ≥ 0

ó (x² – 1) + (x – 2)² ≥ 0

Dấu = xảy ra ó $\{\begin{cases} x^{2} - 1 = 0 \\ x - 2 = 0 \end{cases}$ ó $\{\begin{cases} x = \pm 1 \\ x = 2 \end{cases}$ điều này không xảy ra

=> (x² – 1)² + (x – 2)² > 0 nên B đúng

Đáp án cần chọn là: D

Câu 25:

Tập nghiệm của các bất phương trình x² + 2(x – 3) – 1 > x(x + 5) + 5 và $\frac{2}{3} - \frac{3 x - 6}{2} > \frac{1 + 3 x}{6}$ lần lượt là

A. S₁ = {x|x > -4}; S₂ = {x|x > 7/4}

B. S₁ = {x|x > -4}; S₂ = {x|x < 7/4}

C. S₁ = {x|x < -4}; S₂ = {x|x < 7/4}

D. S₁ = {x|x < -4}; S₂ = {x|x > 7/4}

Xem đáp án

+) x² + 2(x – 3) – 1 > x(x + 5) + 5

ó x² + 2x – 6 – 1 > x² + 5x + 5

ó x² + 2x – x² – 5x > 5 + 6 + 1

ó -3x > 12

ó x < -4

Vậy tập nghiệm của bất phương trình trên là S₁ = {x|x < -4}

+) $\frac{2}{3} - \frac{3 x - 6}{2} > \frac{1 + 3 x}{6}$

ó 2.2 – 3(3x – 6) > 1 + 3x

ó 4 – 9x + 18 > 1 + 3x

ó 12x < 21 ó x < 7/4

Vậy tập nghiệm của bất phương trình trên là S₂ = {x|x < 7/4}

Đáp án cần chọn là: C

Câu 26:

Tích các nghiệm của phương trình |x² + 2x – 1| = 2 là

A. 3

B. -3

C. 1

D. -1

Xem đáp án

Câu 27:

Giải phương trình |x – 3y|²⁰¹⁷ + |y + 4|²⁰¹⁸ = 0 ta được nghiệm (x; y). Khi đó y – x bằng

A. -16

B. -8

C. 16

D. 8

Xem đáp án

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Toán 8 Bài tập Ôn tập chương 4 (Có đáp án)

Trắc nghiệm Toán 8 Bài tập Ôn tập chương 4 (Có đáp án)

Danh sách câu hỏi

Có thể bạn quan tâm

Các bài thi hot trong chương