Đề kiểm tra Học kì 1 Toán 8 có đáp án (Mới nhất)_ đề 4
-
1854 lượt thi
-
6 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Điền chữ Đ hoặc chữ S trong ô vuông tương ứng với mỗi phát biểu sau:
a. ( x + 5 )( x – 5 ) = x2 – 5 c
b. a3 – 1 = (a – 1 ) ( a2 + a + 1 ) c
c. Hình bình hành có một tâm đối xứng là giao điểm của hai đường chéo c
d. Hai tam giác có diện tích bằng nhau thì bằng nhau c
 Xem đáp án
Xem đáp án
1 – S;
2 – Đ;
3 – Đ;
4 – S.
Câu 2:
Khoanh tròn chữ cái trước câu trả lời đúng nhất:
1. Đa thức x2 – 4x + 4 tại x = 2 có giá trị là:
A. 1
B. 0
C. 4
D. 25
2. Giá trị của x để x ( x + 1) = 0 là:
A. x = 0
B. x = - 1
C. x = 0; x = 1
D. x = 0; x = -1
3. Một hình thang có độ dài hai đáy là 6 cm và 10 cm. Độ dài đường trung bình của hình thang đó là :
A. 14 cm
B. 7 cm
C. 8 cm
D. Một kết quả khác.
4. Một tam giác đều cạnh 2 dm thì có diện tích là:
A. dm2
B. 2dm2
C. dm2
D. 6dm2
 Xem đáp án
Xem đáp án
Câu 4:
Cho phân thức:
a) Tìm điều kiện xác định của phân thức A.
b) Thu gọn biểu thức A
c) Tính giá trị của biểu thức A với .
 Xem đáp án
Xem đáp án
a.
c. Thay vào biểu thức A, ta được:
Câu 5:
 Xem đáp án
Xem đáp án
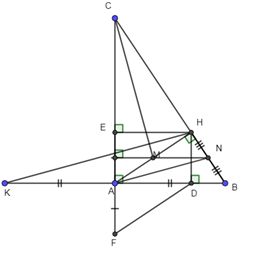
a) vuông tại A
(định lý Py–ta–go)
b) Tứ giác ADHE có: (gt)
Do đó tứ giác ADHE là hình chữ nhật (dấu hiệu nhận biết).
c) Ta có (gt), AE=DH (tứ giác ADHE là hình chữ nhật)
Tứ giác AFDH có AF//DH, AF=DH
suy ra Tứ giác AFDH là hình bình hành (dấu hiệu nhận biết).d) Gọi N là trung điểm của đoạn thẳng BH
Ta có M, N lần lượt là trung điểm của AH, BH
Suy ra MN là đường trung bình của tam giác HAB
Mà
Nên
có MN, AH là hai đường cao cắt nhau tại M
M là trực tâm của tam giác CAN
CM là đường cao của tam giác CAN
Mặt khác A, N lần lượt là trung điểm của BK, HB
AN là đường trung bình của tam giác BKH
Ta có ,
VậyCâu 6:
Cho các số x, y thoả mãn đẳng thức . Tính giá trị của biểu thức
.
 Xem đáp án
Xem đáp án
Biến đổi
Vì với mọi x,
Thay x = 1 và y = -1 vào M
.