Giải SGK Toán 8 CTST Bài 1. Định lí Pythagore có đáp án
-
127 lượt thi
-
22 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
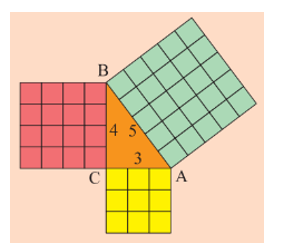
Hãy so sánh diện tích hình vuông màu xanh với tổng diện tích của hai hình vuông màu đỏ và màu vàng.
 Xem đáp án
Xem đáp án
Lời giải:
Hình vuông màu xanh có diện tích là: 52 = 25 (đơn vị diện tích).
Hình vuông màu đỏ có diện tích là: 42 = 16 (đơn vị diện tích).
Hình vuông màu vàng có diện tích là: 32 = 9 (đơn vị diện tích).
Tổng diện tích của hai hình vuông màu đỏ và màu vàng là: 16 + 9 = 25 (đơn vị diện tích).
Vậy diện tích hình vuông màu xanh bằng tổng diện tích của hai hình vuông màu đỏ và màu vàng.
Câu 2:
Cho một tam giác vuông có hai cạnh góc vuông là a, b và cạnh huyền là c.
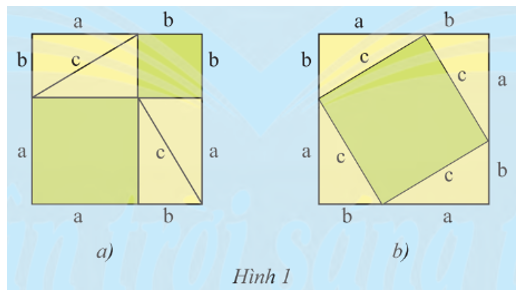
‒ Lấy một tờ bìa lớn, cắt tám hình tam giác vuông bằng tam giác vuông đã cho và cắt hai hình vuông lớn cùng có cạnh bằng a + b.
‒ Đặt bốn tam giác vuông lên hình vuông thứ nhất như trong Hình 1a. Phần bìa không bị che lấp gồm hai hình vuông có cạnh lần lượt là a và b. Tính diện tích phần bìa đó theo a và b.
‒ Đặt bốn tam giác vuông còn lại lên hình vuông thứ hai như trong Hình 1b. Phần bìa không bị che lấp là hình vuông có cạnh là c. Tính diện tích phần bìa đó theo c.
‒ Rút ra kết luận về quan hệ giữa a2 + b2 và c2.
 Xem đáp án
Xem đáp án
• Diện tích hình vuông có cạnh bằng a là: a2 (đơn vị diện tích).
Diện tích hình vuông có cạnh bằng b là: b2 (đơn vị diện tích).
Diện tích phần bìa không bị che lấp trong hình vuông lớn ở Hình 1a là:
a2 + b2 (đơn vị diện tích).
• Diện tích phần bìa không bị che lấp trong hình vuông lớn ở Hình 1b chính là diện tích hình vuông có cạnh bằng c, và bằng: c2 (đơn vị diện tích).
• Trong cả hai hình đều đặt bốn tam giác vuông lên hai hình vuông lớn có cạnh bằng a + b.
Khi đó diện tích phần bìa không bị che lấp của cả hai hình sẽ bằng nhau.
Do đó a2 + b2 = c2.
Câu 3:
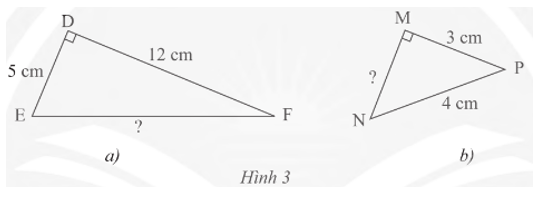
Tính độ dài cạnh EF, MN của các tam giác vuông trong Hình 3.
 Xem đáp án
Xem đáp án
Hình 3a: Áp dụng định lí Pythagore vào tam giác vuông DEF có cạnh huyền EF, ta có:
EF2 = DE2 + DF2
Suy ra EF2 = 52 + 122 = 25 + 144 = 169 = 132.
Vậy EF = 13 cm.
Hình 3b: Áp dụng định lí Pythagore vào tam giác vuông MNP có cạnh huyền NP, ta có:
NP2 = MN2 + MP2
Suy ra MN2 = NP2 – MP2
MN2 = 42 – 32 = 16 – 9 = 7.
Vậy EF = cm.
Câu 4:
Một chiếc ti vi màn hình phẳng có chiều rộng và chiều dài đo được lần lượt là 72 cm và 120 cm. Tính độ dài đường chéo của màn hình chiếc ti vi đó theo đơn vị inch (biết 1 inch ≈ 2,54 cm).

 Xem đáp án
Xem đáp án
Chiếc ti vi ở Hình 4 được mô tả bởi tam giác ABC vuông tại A có các kích thước như hình vẽ sau:
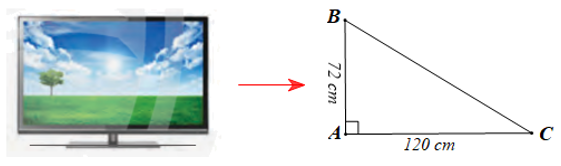
Áp dụng định lí Pythagore vào tam giác ABC có cạnh huyền BC, ta có:
BC2 = AB2 + AC2 = 722 + 1202 = 5 184 + 14 400 = 19 584.
Suy ra BC = (cm).
Vậy độ dài đường chéo của màn hình chiếc ti vi đó theo đơn vị inch là:
(inch).
Câu 5:
 Xem đáp án
Xem đáp án
Ta vẽ tam giác ABC có AB = 12 cm, AC = 5 cm, BC = 13 cm như sau:
• Vẽ đoạn thẳng AB = 12 cm;
• Vẽ cung tròn tâm A bán kính 5 cm và cung tròn tâm B bán kính 13 cm. Hai cung tròn này cắt nhau tại một điểm, điểm này là điểm C.
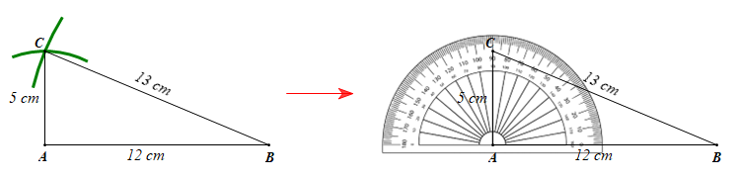
Dùng thước đo góc (đặt thước như hình vẽ trên) ta xác định được .
Câu 6:
Tìm tam giác vuông trong các tam giác sau:
a) Tam giác EFK có EF = 9 m, FK = 12 m, EK = 15 m.
 Xem đáp án
Xem đáp án
a) Ta có: 152 = 92 + 122, suy ra EK2 = EF2 + FK2.
Vậy tam giác EFK vuông tại F.
Câu 7:
b) Tam giác PQR có PQ = 17 cm, QR = 12 cm, PR = 10 cm.
 Xem đáp án
Xem đáp án
b) Ta có PQ là cạnh dài nhất và 172 ≠ 102 + 122, suy ra PQ2 ≠ PR2 + QR2.
Vậy tam giác PQR không phải là tam giác vuông.
Câu 8:
c) Tam giác DEF có DE = 8 m, DF = 6 m, EF = 10 m.
 Xem đáp án
Xem đáp án
c) Ta có: 102 = 62 + 82, suy ra EF2 = DF2 + DE2.
Vậy tam giác DEF vuông tại D.
Câu 9:
a) Nam dự định làm một cái êke từ ba thanh nẹp gỗ. Nam đã có hai thanh làm hai cạnh góc vuông dài 6 cm và 8 cm. Hỏi thanh nẹp còn lại Nam phải làm có độ dài bao nhiêu? (Giả sử các mối nối không đáng kể)
 Xem đáp án
Xem đáp án
a) Giả sử chiếc êke mà Nam dự định làm được mô tả bởi tam giác ABC vuông tại A có kích thước như hình vẽ dưới đây:
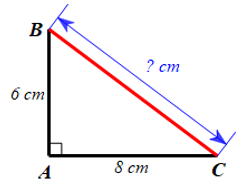
Áp dụng định lí Pythagore cho tam giác ABC có BC là cạnh huyền, ta có:
BC2 = AB2 + AC2 = 62 + 82 = 36 + 64 = 100 = 102
Suy ra BC = 10 cm.
Vậy thanh nẹp còn lại Nam phải làm có độ dài 10 cm.
Câu 10:
b) Một khung gỗ ABCD (Hình 6) được tạo thành từ 5 thanh nẹp có độ dài như sau: AB = CD = 36 cm; BC = AD = 48 cm; AC = 60 cm. Chứng minh rằng và là các góc vuông.
 Xem đáp án
Xem đáp án
b) Xét DABC có: AB2 + BC2 = 362 + 482 = 3600 và AC2 = 602 = 3600.
Do đó AB2 + BC2 = AC2.
Vậy tam giác ABC vuông tại B nên là góc vuông.
Xét DADC có: AD2 + DC2 = 482 + 362 = 3600 và AC2 = 602 = 3600.
Do đó AD2 + DC2 = AC2.
Vậy tam giác ADC vuông tại D nên là góc vuông.
Câu 11:
Tính các độ dài PN và BC trong Hình 9.
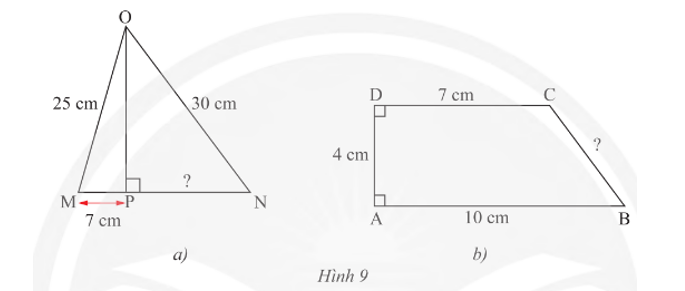
 Xem đáp án
Xem đáp án
a) Áp dụng định lí Pythagore vào tam giác OPM vuông tại P, ta có:
OM2 = OP2 + MP2
Suy ra OP2 = OM2 – MP2 = 252 – 72 = 625 – 49 = 576.
Áp dụng định lí Pythagore vào tam giác OPN vuông tại P, ta có:
ON2 = OP2 + PN2
Suy ra PN2 = ON2 – OP2 = 302 – 576 = 900 – 576 = 324 = 182.
Vậy PN = 18 cm.
b)
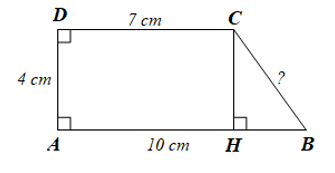
Vẽ CH vuông góc với AB như hình vẽ, ta có:
CH = 4 cm; HB = 10 – 7 = 3 (cm).
Áp dụng định lí Pythagore vào tam giác CHB vuông tại H, ta có:
BC2 = CH2 + HB2 = 42 + 32 = 25 = 52.
Vậy BC = 5 cm.
Câu 12:
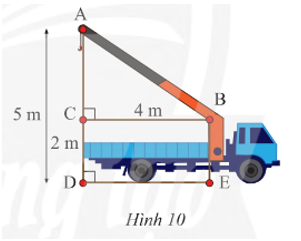
Tính chiều dài cần cẩu AB trong Hình 10.
 Xem đáp án
Xem đáp án
Xét tam giác ABC có CB = 4 m, AC = AD – CD = 5 – 2 = 3 (m).
Áp dụng định lí Pythagore cho tam giác ABC vuông tại C, ta có:
AB2 = AC2 + CB2 = 32 + 42 = 25 = 52.
Suy ra AB = 5 m.
Vậy chiều dài cần cẩu AB là 5 m.
Câu 13:
Cho tam giác ABC vuông tại A.
a) Tính độ dài cạnh BC nếu biết AB = 7 cm, AC = 24 cm.
 Xem đáp án
Xem đáp án
a) Áp dụng định lí Pythagore cho tam giác ABC vuông tại A, ta có:
BC2 = AB2 + AC2 = 72 + 242 = 49 + 576 = 625 = 252.
Vậy BC = 25 cm.
Câu 14:
b) Tính độ dài cạnh AB nếu biết AC = 2 cm, BC = cm.
 Xem đáp án
Xem đáp án
b) Áp dụng định lí Pythagore cho tam giác ABC vuông tại A, ta có:
BC2 = AB2 + AC2.
Suy ra AB2 = BC2 – AC2 = – 22 = 13 – 4 = 9 = 32.
Vậy AB = 3 cm.
Câu 15:
c) Tính độ dài cạnh AC nếu biết BC = 25 cm, AB = 15 cm.
 Xem đáp án
Xem đáp án
c) Áp dụng định lí Pythagore cho tam giác ABC vuông tại A, ta có:
BC2 = AB2 + AC2.
Suy ra: AC2 = BC2 – AB2 = 252 – 152 = 625 – 225 = 400 = 202.
Vậy AC = 20 cm.
Câu 16:
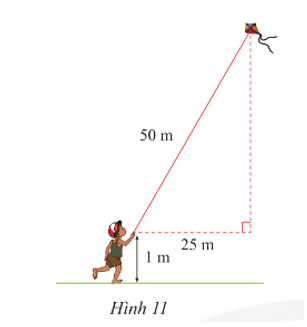
Tính độ cao của con diều so với mặt đất (Hình 11).
 Xem đáp án
Xem đáp án
Đặt các điểm A, B, C như hình vẽ trên.
Áp dụng định lí Pythagore cho tam giác ABC vuông tại A, ta có:
BC2 = AB2 + AC2.
Suy ra: AC2 = BC2 – AB2 = 502 – 252 = 2 500 – 625 = 1 875 = .
Do đó AC = (m).
Vậy độ cao của con diều so với mặt đất là: (m).
Câu 17:
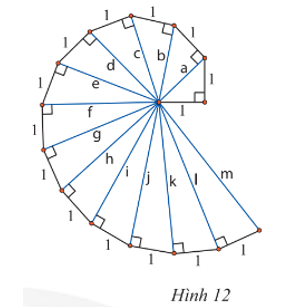
Lần lượt tính độ dài các cạnh huyền a, b, c, d của các tam giác vuông trong Hình 12. Hãy dự đoán kết quả của các cạnh huyền còn lại.
 Xem đáp án
Xem đáp án
Áp dụng định lí Pythagore lần lượt cho các tam giác vuông có cạnh huyền a, b, c, d trong Hình 12 ta có:
• a2 = 12 + 12 = 2, suy ra a = ;
• b2 = a2 + 12 = 2 + 1 = 3, suy ra b = .
• c2 = b2 + 12 = 3 + 1 = 4, suy ra c = .
• d2 = c2 + 12 = 4 + 1 = 5, suy ra d = .
Dự đoán kết quả của các cạnh huyền còn lại:
.
Câu 18:
Chứng minh rằng tam giác ABC vuông trong các trường hợp sau:
a) AB = 8 cm, AC = 15 cm, BC = 17 cm;
 Xem đáp án
Xem đáp án
a) Ta có: 172 = 82 + 152. Suy ra BC2 = AB2 + AC2.
Vậy tam giác ABC vuông tại A.
Câu 19:
Chứng minh rằng tam giác ABC vuông trong các trường hợp sau:
b) AB = 29 cm, AC = 21 cm, BC = 20 cm;
 Xem đáp án
Xem đáp án
b) Ta có 292 = 202 + 212. Suy ra AB2 = BC2 + AC2.
Vậy tam giác ABC vuông tại C.
Câu 20:
Chứng minh rằng tam giác ABC vuông trong các trường hợp sau:
c) AB = 12 cm, AC = 37 cm, BC = 35 cm.
 Xem đáp án
Xem đáp án
c) Ta có 372 = 122 + 352. Suy ra AC2 = AB2 + BC2.
Vậy tam giác ABC vuông tại B.
Câu 21:
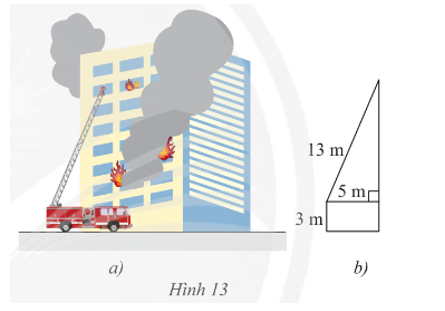
Cho biết thang của một xe cứu hoả có chiều dài 13 m, chân thang cách mặt đất 3 m và cách tường của toà nhà 5 m. Tính chiều cao mà thang có thể vươn tới.
 Xem đáp án
Xem đáp án
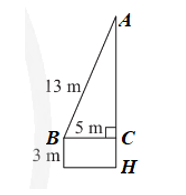
Đặt các điểm A, B, C, H như hình vẽ trên.
Áp dụng định lí Pythagore cho tam giác ABC vuông tại C, ta có:
AB2 = AC2 + BC2.
Suy ra: AC2 = AB2 – BC2 = 132 – 52 = 169 – 25 = 144 = 122.
Do đó AC = 12 m và AH = 12 + 3 = 15 (m).
Vậy chiều cao mà thang có thể vươn tới là 15 m.
Câu 22:
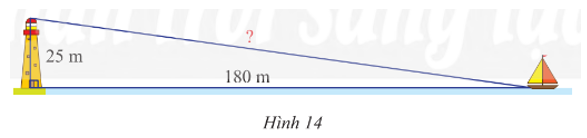
Một con thuyền đang neo ở một điểm cách chân tháp hải đăng 180 m. Cho biết tháp hải đăng cao 25 m. Hãy tính khoảng cách từ thuyền đến ngọn hải đăng.
 Xem đáp án
Xem đáp án
Đặt các điểm A, B lần lượt là vị trí của đỉnh tháp hải đăng, chân tháp hải đăng và C là vị trí của con thuyền.
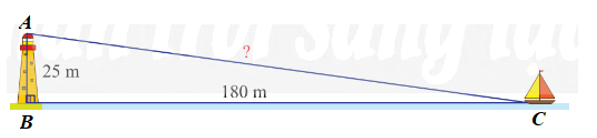
Áp dụng định lí Pythagore cho tam giác ABC vuông tại B, ta có:
AC2 = AB2 + BC2 = 252 + 1802 = 625 + 32 400 = 33 025.
Suy ra AC ≈ 181,73 (m).
Vậy khoảng cách từ thuyền đến ngọn hải đăng khoảng 181,73 m.
