Giải SGK Toán 8 CTST Bài 1. Đơn thức và đa thức nhiều biến có đáp án
-
274 lượt thi
-
29 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Hình bên là bản vẽ sơ lược nền của một ngôi nhà (các kích thước tính theo m).
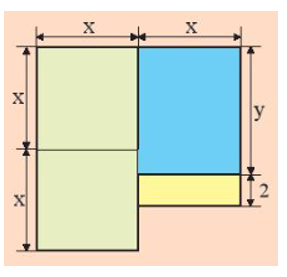
Có thể biểu thị diện tích của nền nhà bằng một biểu thức chứa x và y không? Nếu có, trong biểu thức đó chứa các phép tính nào?
 Xem đáp án
Xem đáp án
Có thể biểu thị diện tích của nền nhà bằng một biểu thức chứa x và y.
Ta chia nền nhà thành các hình chữ nhật ABCD, BEFG, GHKF như hình vẽ dưới đây.
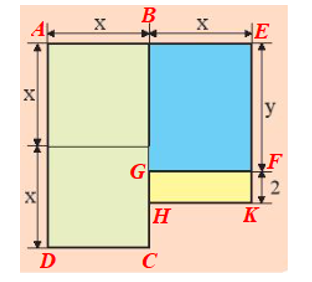
Biểu thức biểu thị diện tích hình chữ nhật ABCD là:
(x + x).x = 2x.x = 2x2 (m2).
Biểu thức biểu thị diện tích hình chữ nhật BEFG là: xy (m2).
Biểu thức biểu thị diện tích hình chữ nhật GHKF là: 2x (m2).
Diện tích nền nhà là tổng diện tích của các hình chữ nhật nên biểu thức biểu thị diện tích nền nhà là:
2x2 + xy + 2x (m2).
Trong biểu thức trên có chứa phép cộng, phép nhân.
Câu 2:
Một số biểu thức được phân chia thành các nhóm như dưới đây:
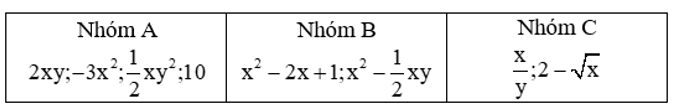
a) Các biểu thức ở nhóm A có đặc điểm gì phân biệt với các biểu thức ở nhóm B và nhóm C?
 Xem đáp án
Xem đáp án
a) Các biểu thức ở nhóm A là các biểu thức đại số chỉ gồm một số, hoặc một tích giữa các số và các biến.
Các biểu thức ở nhóm B và nhóm C là tổng, hiệu hoặc thương của các biểu thức đại số gồm một số, hoặc một tích giữa các số và các biến.
Câu 3:
b) Các biểu thức ở nhóm A và nhóm B có đặc điểm gì chung, phân biệt với các biểu thức ở nhóm C?
 Xem đáp án
Xem đáp án
b) Các biểu thức ở nhóm A và nhóm B chỉ gồm tổng, hiệu hoặc tích giữa các số và các biến.
Các biểu thức ở nhóm C có xuất hiện phép chia giữa các biến hoặc phép toán lấy căn bậc hai số học của biến.
Câu 4:
Cho các biểu thức sau:
a) Các đơn thức;
 Xem đáp án
Xem đáp án
Trong các biểu thức trên:
a) Các đơn thức là: .
Câu 5:
b) Các đa thức và số hạng tử của chúng.
 Xem đáp án
Xem đáp án
b) Các đa thức là: ; ab – πr2 và x3 – x + 1.
Các đa thức đều có một hạng tử.
Đa thức ab – πr2 có hai hạng tử; đa thức x3 – x + 1 có ba hạng tử.
Câu 6:
Một bức tường hình thang có cửa sổ hình tròn với các kích thước như Hình 1 (tính bằng m)
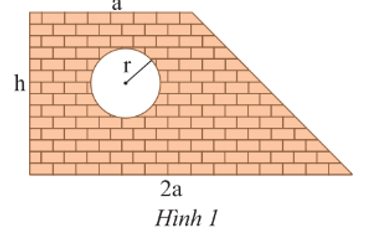
a) Viết biểu thức biểu thị diện tích bức tường (không tính phần cửa sổ).
 Xem đáp án
Xem đáp án
a) Biểu thức biểu thị diện tích bức tường hình thang (tính cả phần cửa sổ) là:
(m2).
Biểu thức biểu thị diện tích của cửa sổ hình tròn là: πr2 (m2).
Biểu thức biểu thị diện tích bức tường không tính phần cửa sổ là:
ah – πr2 (m2).
Câu 7:
b) Tính giá trị diện tích trên khi a = 2 m; h = 3 m; r = 0,5 m (lấy π = 3,14; làm tròn kết quả đến hàng phần trăm).
 Xem đáp án
Xem đáp án
b) Thay a = 2 m; h = 3 m; r = 0,5 m vào biểu thức ở câu a và lấy π = 3,14 ta có:
.2.3 – 3,14.0,52 = 9 – 0,785 = 8,215 (m2).
Làm tròn kết quả đến hàng phần trăm ta được diện tích bức tường không tính phần cửa sổ là 8,22 (m2).
Câu 8:
 Xem đáp án
Xem đáp án
Thể tích của hình hộp chữ nhật có ba kích thước a, b, c là: V = abc (đơn vị thể tích).
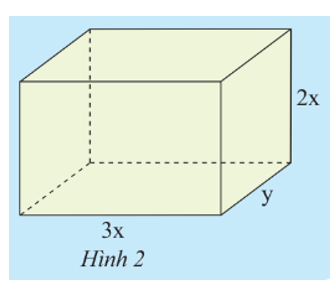
Do đó thể tích của hình hộp chữ nhật ở Hình 2 là:
V = 3x.y.2x = 3xy.2x = (3.2).(x.x).y = 6.x1+1.y = 6x2y (đơn vị thể tích).
Vậy kết quả của hai bạn An và Tâm đều đúng, tuy nhiên kết quả của bạn Tâm gọn hơn.
Câu 9:
Thu gọn các đơn thức sau đây. Chỉ ra hệ số và bậc của chúng.
a) 12xy2x; Xem đáp án
Xem đáp án
a) 12xy2x = 12.(x.x).y2 = 12x2y2.
Câu 10:
Thu gọn các đơn thức sau đây. Chỉ ra hệ số và bậc của chúng.
b) –y(2z)y;
 Xem đáp án
Xem đáp án
b) –y(2z)y = –2.(y.y).z = –2y2z.
Câu 11:
Thu gọn các đơn thức sau đây. Chỉ ra hệ số và bậc của chúng.
c) x3yx; Xem đáp án
Xem đáp án
c) x3yx = (x3.x).y = x4y.
Câu 12:
Thu gọn các đơn thức sau đây. Chỉ ra hệ số và bậc của chúng.
d) 5x2y3z4y. Xem đáp án
Xem đáp án
d) 5x2y3z4y = 5x2.(y3.y).z4 = 5x2y4z4.
Câu 13:
Cho hai hình hộp chữ nhật A và B có các kích thước như Hình 3
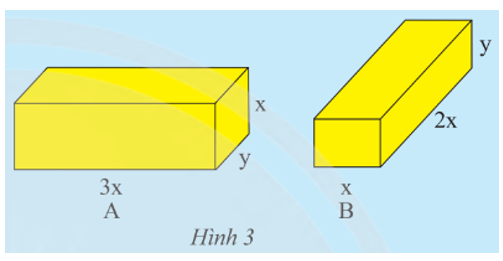
a) Tính tổng thể tích của hình hộp chữ nhật A và B.
 Xem đáp án
Xem đáp án
a) Thể tích của hình hộp chữ nhật A là:
3x.y.x = 3x2y (đơn vị thể tích).
Thể tích của hình hộp chữ nhật B là:
x.2x.y = 2x2y (đơn vị thể tích).
Tổng thể tích của hình hộp chữ nhật A và B là:
3x2y + 2x2y = (3 + 2)x2y = 5x2y (đơn vị thể tích).
Câu 14:
b) Thể tích của A lớn hơn thể tích của B bao nhiêu?
 Xem đáp án
Xem đáp án
b) Thể tích của A lớn hơn thể tích của B là:
3x2y – 2x2y = (3 – 2)x2y = x2y (đơn vị thể tích).
Câu 15:
Mỗi cặp đơn thức sau có đồng dạng không? Nếu có, hãy tìm tổng và hiệu của chúng.
a) xy và –6xy;
 Xem đáp án
Xem đáp án
a) xy và –6xy là hai đơn thức đồng dạng vì có hệ số khác 0 và cùng có phần biến là xy.
Câu 16:
Mỗi cặp đơn thức sau có đồng dạng không? Nếu có, hãy tìm tổng và hiệu của chúng.
b) 2xy và xy2;
 Xem đáp án
Xem đáp án
b) Đơn thức 2xy có phần biến là xy;
Đơn thức xy2 có phần biến là xy2.
Phần biến của hai đơn thức khác nhau nên hai đơn thức 2xy và xy2 không phải là hai đơn thức đồng dạng.
Câu 17:
Mỗi cặp đơn thức sau có đồng dạng không? Nếu có, hãy tìm tổng và hiệu của chúng.
c) –4yzx2 và 4x2yz.
 Xem đáp án
Xem đáp án
c) Ta có –4yzx2 = –4x2yz, đơn thức này có phần biến là x2yz;
Đơn thức 4x2yz có phần biến là x2yz.
Vậy hai đơn thức có hệ số khác 0 và có cùng phần biến nên là hai đơn thức đồng dạng.
Câu 18:
Cho hai đa thức A = 5x2 – 4xy + 2x – 4x2 + xy; B = x2 – 3xy + 2x.
Tính giá trị của A và B tại x = –2; y = . So sánh hai kết quả nhận được.
 Xem đáp án
Xem đáp án
• Thay x = –2 và y = vào đa thức A = 5x2 – 4xy + 2x – 4x2 + xy ta được:
A = 5.(–2)2 – 4.(–2). + 2.(–2) – 4.(–2)2 + (–2).
= 20 + – 4 – 16 –
= 2.
• Thay x = –2 và y = vào đa thức B = x2 – 3xy + 2x ta được:
B = (–2)2 – 3.(–2). + 2.(–2) = 4 + 2 – 4 = 2.
Vậy giá trị của hai biểu thức A và B bằng nhau.
Câu 19:
Thu gọn và tìm bậc của mỗi đa thức sau:
a) A = x – 2y + xy – 3x + y2;
 Xem đáp án
Xem đáp án
a) A = x – 2y + xy – 3x + y2
= (x – 3x) – 2y + xy + y2
= –2x – 2y + xy + y2
Bốn hạng tử của A lần lượt có bậc là 1; 1; 2; 2. Do đó bậc của đa thức A bằng 2.
Câu 20:
Thu gọn và tìm bậc của mỗi đa thức sau:
b) B = xyz – x2y + xz – xyz + xz.
 Xem đáp án
Xem đáp án
b) B = xyz – x2y + xz – xyz + xz
Ba hạng tử của B lần lượt có bậc là 3; 3; 2. Do đó bậc của đa thức B bằng 3.
Câu 21:
Tính giá trị của đa thức A = 3x2y – 5xy – 2x2y – 3xy tại x = 3; y = .
 Xem đáp án
Xem đáp án
Thu gọn đa thức A:
A = 3x2y – 5xy – 2x2y – 3xy
= (3x2y – 2x2y) + (– 5xy – 3xy)
= x2y – 8xy
Thay x = 3 và y = vào đa thức A thu gọn ở trên ta được:
.
Câu 22:
Cho hình hộp chữ nhật có các kích thước như Hình 4 (tính theo cm).
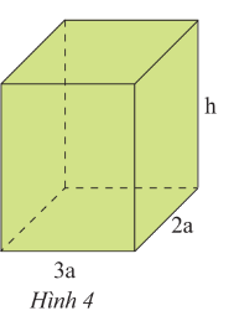
a) Viết các biểu thức tính thể tích và diện tích xung quanh của hình hộp chữ nhật đó.
 Xem đáp án
Xem đáp án
a) Biểu thức biểu thị thể tích của hình hộp chữ nhật đó là:
V = 3a.2a.h = 6a2h (cm3).
Biểu thức biểu thị diện tích xung quanh của hình hộp chữ nhật đó là:
Sxq = 2.(3a + 2a).h = 2.5a.h = 10ah (cm2).
Câu 23:
b) Tính giá trị của các đại lượng trên khi a = 2 cm; h = 5 cm.
 Xem đáp án
Xem đáp án
b) Thay a = 2 cm và h = 5 cm vào biểu thức V = 6a2h ta được:
V = 6.22.5 = 120 (cm3).
Thay a = 2 cm và h = 5 cm vào biểu thức Sxq = 10ah ta được:
Sxq = 10.2.5 = 100 (cm2).
Vậy khi a = 2 cm; h = 5 cm thì thể tích và diện tích xung quanh của hình hộp chữ nhật lần lượt là 120 cm3 và 100 cm2.
Câu 24:
Chỉ ra các đơn thức, đa thức trong các biểu thức sau:
. Xem đáp án
Xem đáp án
Các đơn thức là: –3; 2z; –10x2yz.
Các đa thức là: –3; 2z; –10x2yz; xy + 1; 5x – .
Câu 25:
Thu gọn các đơn thức sau. Chỉ ra hệ số, phần biến và bậc của mỗi đơn thức.
. Xem đáp án
Xem đáp án
Thu gọn các đơn thức:
• 5xyx = 5(x.x)y = 5x2y;
• –xyzy = –x(y.y)z = –xy2z;
• .
Ta có:
|
Đơn thức |
Hệ số |
Phần biến |
Bậc |
|
5x2y |
5 |
x2y |
3 |
|
– xy2z |
|
xy2z |
4 |
|
x3 |
|
x3 |
3 |
Câu 26:
Thu gọn và tìm bậc của mỗi đa thức sau:
a) M = x – 3 – 4y + 2x – y;
 Xem đáp án
Xem đáp án
a) M = x – 3 – 4y + 2x – y
= (x + 2x) + (–4y – y) – 3
= 3x – 5y – 3
Ba hạng tử của đa thức M có bậc lần lượt là 1; 1; 0. Do đó bậc của đa thức M bằng 1.
Câu 27:
Thu gọn và tìm bậc của mỗi đa thức sau:
b) N = –x2t + 13t3 + xt2 + 5t3 – 4.
 Xem đáp án
Xem đáp án
b) N = –x2t + 13t3 + xt2 + 5t3 – 4.
= –x2t + (13t3 + 5t3) + xt2 – 4
= –x2t + 18t3 + xt2 – 4
Câu 28:
Tính giá trị của đa thức P = 3xy2 – 6xy + 8xz + xy2 – 10xz tại x = –3; y = ; z = 3.
 Xem đáp án
Xem đáp án
Thu gọn đa thức P:
P = 3xy2 – 6xy + 8xz + xy2 – 10xz
= (3xy2 + xy2) – 6xy + (8xz – 10xz)
= 4xy2 – 6xy – 2xz.
Thay x = –3; y = và z = 3 vào đa thức P ta được:
Vậy giá trị của biểu thức P đã cho tại x = –3; y = ; z = 3 là 6.
Câu 29:
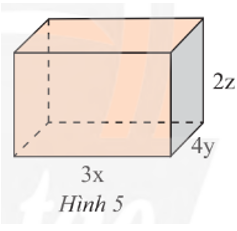
Viết biểu thức biểu thị thể tích V và diện tích xung quanh S của hình hộp chữ nhật trong Hình 5.
Tính giá trị của V, S khi x = 4 cm, y = 2 cm và z = 1 cm.
 Xem đáp án
Xem đáp án
Biểu thức biểu thị thể tích V của hình hộp chữ nhật trong Hình 5 là:
V = 3x.4y.2z = 24xyz (đơn vị thể tích).
Biểu thức biểu thị diện tích xung quanh S của hình hộp chữ nhật trong Hình 5 là:
S = 2.(3x + 4y).2z = 4z(3x + 4y) (đơn vị diện tích).
Thay x = 4 cm, y = 2 cm và z = 1 cm vào biểu thức V, S ta được:
V = 24xyz = 24.4.2.1 = 192 (cm3).
S = 4.1.(3.4 + 4.2) = 4.(12 + 8) = 80 (cm2).
