Giải SGK Toán 8 CTST Bài 4. Phân tích đa thức thành nhân tử có đáp án
-
172 lượt thi
-
38 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Phát biểu của bạn nữ: “993 – 99 chia hết cho cả ba số 98, 99 và 100.”
Phát biểu của bạn nam: “Đúng rồi. Vì n3 – n chia hết cho n, n – 1 và n + 1 mà. (n là số tự nhiên, n > 1)”
Phát biểu của hai bạn có đúng không? Vì sao?
 Xem đáp án
Xem đáp án
Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:
Ta có: 993 – 99 = 99.(992 – 1)
= 99.(992 – 12)
= 99.(99 – 1).(99 + 1)
= 99.98.100
Do đó 993 – 99 chia hết cho cả ba số 98, 99 và 100.
Ta có: n3 – n = n(n2 – 1)
= n.(n – 1).(n + 1)
Do đó n3 – n chia hết cho n, n – 1 và n + 1.
Vậy phát biểu của cả hai bạn đều đúng.
Câu 2:
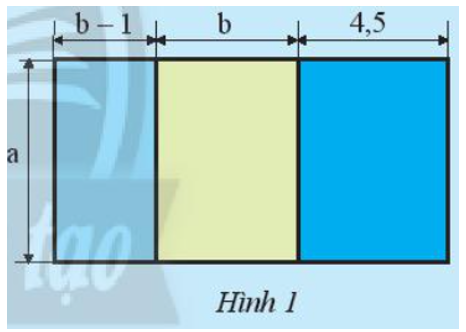
Tính diện tích của nền nhà có bản vẽ sơ lược như Hình 1 theo những cách khác nhau, biết a = 5; b = 3,5 (các kích thước tính theo mét).
Tính theo cách nào nhanh hơn?
 Xem đáp án
Xem đáp án
Cách 1: Tính tổng diện tích các hình.
Diện tích hình chữ nhật có chiều dài a (m) và chiều rộng b – 1 (m) là: a(b – 1) (m2).
Diện tích hình chữ nhật có chiều dài a (m) và chiều rộng b (m) là: ab (m2).
Diện tích hình chữ nhật có chiều dài a (m) và chiều rộng 4,5 (m) là: 4,5a (m2).
Diện tích của nền nhà là: S = a(b – 1) + ab + 4,5a (m2).
Với a = 5 và b = 3,5 ta có:
S = 5.(3,5 – 1) + 5.3,5 + 4,5.5
= 5 . (3,5 – 1 + 3,5 + 4,5)
= 5 . 10,5
= 52,5 (m2).
Cách 2: Tính chiều dài của nền nhà rồi tính diện tích của nền nhà.
Chiều dài của nền nhà là:
b – 1 + b + 4,5 = 2b + 3,5 (m).
Diện tích của nền nhà là: S = a.(2b + 3,5) (m2).
Với a = 5 và b = 3,5 ta có:
S = 5.(2.3,5 + 3,5) = 5 . 10,5 = 52,5 (m2).
Chú ý: Ngoài 2 cách trên ta có thể tính diện tích của nền nhà theo cách khác.
Trong tất cả các cách thì ta thấy Cách 2 là nhanh nhất.
Câu 3:
Phân tích các đa thức sau thành nhân tử:
a) P = 6x – 2x3;
 Xem đáp án
Xem đáp án
a) P = 6x – 2x3
= 2x.3 – 2x.x2
= 2x(3 – x2).
Câu 4:
Phân tích các đa thức sau thành nhân tử:
b) Q = 5x3 – 15x2y;
 Xem đáp án
Xem đáp án
b) Q = 5x3 – 15x2y
= 5x2.x – 5x2.3y
= 5x2(x – 3y).
Câu 5:
Phân tích các đa thức sau thành nhân tử:
c) R = 3x3y3 – 6xy3z + xy.
 Xem đáp án
Xem đáp án
c) R = 3x3y3 – 6xy3z + xy
= xy.3x2y2 – xy.6y2z + xy.1
= xy(3x2y2 – 6y2z + 1).
Câu 6:
Tìm biểu thức thích hợp thay vào mỗi chỗ , từ đó hoàn thành biến đổi sau vào vở để phân tích đa thức sau thành nhân tử:
a) ;
 Xem đáp án
Xem đáp án
a,
Câu 7:
Tìm biểu thức thích hợp thay vào mỗi chỗ , từ đó hoàn thành biến đổi sau vào vở để phân tích đa thức sau thành nhân tử:
b)
 Xem đáp án
Xem đáp án
b,
Câu 8:
Phân tích các đa thức sau thành nhân tử:
a) 9x2 – 16;
 Xem đáp án
Xem đáp án
a) 9x2 – 16 = (3x)2 – 42
= (3x – 4)(3x + 4).
Câu 9:
Phân tích các đa thức sau thành nhân tử:
b) 4x2 – 12xy + 9y2; Xem đáp án
Xem đáp án
b) 4x2 – 12xy + 9y2
= (2x)2 – 2.2x.3y + (3y)2
= (2x – 3y)2.
Câu 10:
Phân tích các đa thức sau thành nhân tử:
c) t3 – 8;
 Xem đáp án
Xem đáp án
c) t3 – 8 = t3 – 23
= (t – 2)(t2 + t.2 + 22)
= (t – 2)(t2 – 2t + 4).
Câu 11:
Phân tích các đa thức sau thành nhân tử:
d) 2ax3y3 + 2a.
 Xem đáp án
Xem đáp án
d) 2ax3y3 + 2a
= 2a.(x3y3 + 1)
= 2a.[(xy)3 + 13]
= 2a(xy + 1)[(xy)2 – xy.1 + 12]
= 2a(xy + 1)(x2y2 – xy + 1).
Câu 12:
Tìm một hình hộp chữ nhật có thể tích 2x3 – 18x (với x > 3) mà độ dài các cạnh đều là biểu thức chứa x.
 Xem đáp án
Xem đáp án
Ta có: 2x3 – 18x = 2x(x2 – 9)
= 2x(x2 – 32)
= 2x(x – 3)(x + 3)
Vậy hình hộp chữ nhật có thể tích 2x3 – 18x (với x > 3) sẽ có độ dài ba kích thước là 2x, x – 3 và x + 3.
Câu 13:
Giải đáp câu hỏi ở Hoạt động khởi động (trang 23).
 Xem đáp án
Xem đáp án
Ta có: 993 – 99 = 99.(992 – 1)
= 99.(992 – 12)
= 99.(99 – 1).(99 + 1)
= 99.98.100
Do đó 993 – 99 chia hết cho cả ba số 98, 99 và 100.
Ta có: n3 – n = n(n2 – 1)
= n.(n – 1).(n + 1)
Do đó n3 – n chia hết cho n, n – 1 và n + 1.
Vậy phát biểu của cả hai bạn đều đúng.
Câu 14:
Hãy hoàn thành biến đổi sau vào vở để phân tích đa thức thành nhân tử:
a2 + ab + 2a + 2b = (a2 + ab) + (2a + 2b) = …
Em có thể biến đổi theo cách khác để phân tích đa thức trên thành nhân tử không?
 Xem đáp án
Xem đáp án
a2 + ab + 2a + 2b
= (a2 + ab) + (2a + 2b)
= a(a + b) + 2(a + b)
= (a + b)(a + 2).
Ta có thể biến đổi theo cách khác như sau:
a2 + ab + 2a + 2b
= (a2 + 2a) + (ab + 2b)
= a(a + 2) + b(a + 2)
= (a + 2)(a + b).
Câu 15:
Phân tích các đa thức sau thành nhân tử:
a) a3 – a2b + a – b;
 Xem đáp án
Xem đáp án
a) a3 – a2b + a – b
= (a3 – a2b) + (a – b)
= a2(a – b) + (a – b)
= (a – b)(a2 + 1).
Câu 16:
Phân tích các đa thức sau thành nhân tử:
b) x2 – y2 + 2y – 1.
 Xem đáp án
Xem đáp án
b) x2 – y2 + 2y – 1
= x2 – (y2 – 2y + 1)
= x2 – (y – 1)2
= (x + y – 1).[x – (y – 1)]
= (x + y – 1)(x – y + 1).
Câu 17:
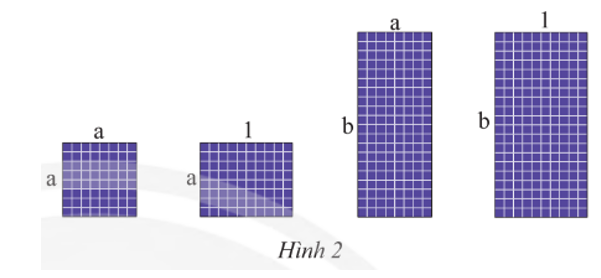
Có thể ghép bốn tấm pin mặt trời với kích thước như Hình 2 thành một hình chữ nhật không? Nếu có, tính độ dài các cạnh và diện tích hình chữ nhật đó. Biết a = 0,8; b = 2 (các kích thước tính theo mét).
 Xem đáp án
Xem đáp án
Diện tích tấm pin hình vuông có cạnh bằng a là: a2 (m2).
Diện tích tấm pin hình chữ nhật có chiều dài bằng 1 và chiều rộng bằng a là: a.1 = a (m2).
Diện tích tấm pin hình chữ nhật có chiều dài bằng b và chiều rộng bằng a là: ab (m2).
Diện tích tấm pin hình chữ nhật có chiều dài bằng b và chiều rộng bằng 1 là: b.1 = b (m2).
Tổng diện tích bốn tấm pin mặt trời là:
S = a2 + a + ab + b = (a2 + a) + (ab + b)
= a(a + 1) + b(a + 1)
= (a + 1)(a + b) (m2).
Vậy có thể ghép bốn tấm pin mặt trời với kích thước như Hình 2 thành một hình chữ nhật có chiều rộng là a + 1 (m) và chiều dài là a + b (m).
Với a = 0,8 (m) và b = 2 (m) ta có:
• Chiều rộng hình chữ nhật đó là 0,8 + 1 = 1,8 (m).
• Chiều dài hình chữ nhật đó là 0,8 + 2 = 2,8 (m).
• Diện tích hình chữ nhật đó là: 1,8 . 2,8 = 5,04 (m2).
Câu 18:
Phân tích các đa thức sau thành nhân tử:
a) x3 + 4x;
 Xem đáp án
Xem đáp án
a) x3 + 4x = x.x2 + x.4 = x(x2 + 4).
Câu 19:
Phân tích các đa thức sau thành nhân tử:
b) 6ab – 9ab2;
 Xem đáp án
Xem đáp án
b) 6ab – 9ab2 = 3ab.2 – 3ab.3b = 3ab(2 – 3b).
Câu 20:
Phân tích các đa thức sau thành nhân tử:
c) 2a(x – 1) + 3b(1 – x);
 Xem đáp án
Xem đáp án
c) 2a(x – 1) + 3b(1 – x)
= 2a(x – 1) + 3b[– (x – 1)]
= 2a(x – 1) – 3b(x – 1)
= (x – 1)(2a – 3b).
Câu 21:
Phân tích các đa thức sau thành nhân tử:
d) (x – y)2 – x(y – x).
 Xem đáp án
Xem đáp án
d) (x – y)2 – x(y – x)
= (x – y)2 + x(x – y)
= (x – y)(x – y + x)
= (x – y)(2x – y).
Câu 22:
Phân tích các đa thức sau thành nhân tử:
a) 4x2 – 1;
 Xem đáp án
Xem đáp án
a) 4x2 – 1 = (2x)2 – 12 = (2x + 1)(2x –1).
Câu 23:
Phân tích các đa thức sau thành nhân tử:
b) (x + 2)2 – 9;
 Xem đáp án
Xem đáp án
b) (x + 2)2 – 9 = (x + 2)2 – 32
= (x + 2 + 3)(x + 2 – 3)
= (x + 5)(x – 1).
Câu 24:
Phân tích các đa thức sau thành nhân tử:
c) (a + b)2 – (a – 2b)2.
 Xem đáp án
Xem đáp án
c) (a + b)2 – (a – 2b)2
= [(a + b) + (a – 2b)] . [(a + b) – (a – 2b)]
= [a + b + a – 2b] . [a + b – a + 2b]
= (2a – b).3b.
Câu 25:
Phân tích các đa thức sau thành nhân tử:
a) 4a2 + 4a + 1;
 Xem đáp án
Xem đáp án
a) 4a2 + 4a + 1
= (2a)2 + 2.2a.1 + 12
= (2a + 1)2.
Câu 26:
Phân tích các đa thức sau thành nhân tử:
b) –3x2 + 6xy – 3y2;
 Xem đáp án
Xem đáp án
b) –3x2 + 6xy – 3y2
= –3(x2 – 2xy + y2)
= –3(x – y)2.
Câu 27:
Phân tích các đa thức sau thành nhân tử:
c) (x + y)2 – 2(x + y)z + z2.
 Xem đáp án
Xem đáp án
c) (x + y)2 – 2(x + y)z + z2
= [(x + y) – z]2
= (x + y – z)2.
Câu 28:
Phân tích các đa thức sau thành nhân tử:
a) 8x3 – 1;
 Xem đáp án
Xem đáp án
a) 8x3 – 1
= (2x)3 – 13
= (2x – 1)[(2x)2 + 2x.1 + 12]
= (2x – 1)(4x2 + 2x + 1).
Câu 29:
Phân tích các đa thức sau thành nhân tử:
b) x3 + 27y3;
 Xem đáp án
Xem đáp án
b) x3 + 27y3
= x3 + (3y)3
= (x + 3y)[x2 – x.3y + (3y)2]
= (x + 3y)(x2 – 3xy + 9y2).
Câu 30:
Phân tích các đa thức sau thành nhân tử:
c) x3 – y6.
 Xem đáp án
Xem đáp án
c) x3 – y6
= x3 – (y2)3
= (x – y2)[x2 + x.y2 + (y2)2]
= (x – y2)(x2 + xy2 + y4).
Câu 31:
Phân tích các đa thức sau thành nhân tử:
a) 4x3 – 16x;
 Xem đáp án
Xem đáp án
a) 4x3 – 16x
= 4x(x2 – 4)
= 4x(x2 – 22)
= 4x(x + 2)(x – 2).
Câu 32:
Phân tích các đa thức sau thành nhân tử:
b) x4 – y4;
 Xem đáp án
Xem đáp án
b) x4 – y4
= (x2)2 – (y2)2
= (x2 + y2)(x2 – y2)
= (x2 + y2)(x + y)(x – y).
Câu 33:
Phân tích các đa thức sau thành nhân tử:
c) xy2 + x2y + y3;
 Xem đáp án
Xem đáp án
c) xy2 + x2y + y3
= y(xy + x2 + y2)
Câu 34:
Phân tích các đa thức sau thành nhân tử:
d) x2 + 2x – y2 + 1.
 Xem đáp án
Xem đáp án
d) x2 + 2x – y2 + 1
= (x2 + 2x + 1) – y2
= (x + 1)2 – y2
= (x + 1 + y)(x + 1 – y).
Câu 35:
Phân tích các đa thức sau thành nhân tử:
a) x2 – xy + x – y;
 Xem đáp án
Xem đáp án
a) x2 – xy + x – y
= (x2 – xy) + (x – y)
= x(x – y) + (x – y)
= (x – y)(x + 1).
Câu 36:
Phân tích các đa thức sau thành nhân tử:
b) x2 + 2xy – 4x – 8y;
 Xem đáp án
Xem đáp án
b) x2 + 2xy – 4x – 8y
= (x2 + 2xy) – (4x + 8y)
= x(x + 2y) – 4(x + 2y)
= (x + 2y)(x – 4).
Câu 37:
Phân tích các đa thức sau thành nhân tử:
c) x3 – x2 – x + 1.
 Xem đáp án
Xem đáp án
c) x3 – x2 – x + 1
= (x3 – x2) – (x – 1)
= x2(x – 1) – (x – 1)
= (x – 1)(x2 – 1)
= (x – 1)(x + 1)(x – 1)
= (x – 1)2(x + 1).
Câu 38:
Cho y > 0. Tìm độ dài cạnh của hình vuông có diện tích bằng 49y2 + 28y + 4.
 Xem đáp án
Xem đáp án
Giả sử hình vuông có độ dài cạnh bằng a (a > 0), khi đó diện tích của hình vuông là a2.
Tức là 49y2 + 28y + 4 = a2.
Ta phân tích đa thức 49y2 + 28y + 4 thành nhân tử có dạng a2.
49y2 + 28y + 4
= (7y)2 + 2.7y.2 + 22
= (7y + 2)2
Vậy độ dài cạnh của hình vuông có diện tích bằng 49y2 + 28y + 4 là 7y + 2.
