Giải SGK Toán 8 KNTT Bài 12. Hình bình hành có đáp án
-
159 lượt thi
-
26 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Hai con đường lớn a và b cắt nhau tạo thành một góc. Bên trong góc đó có một điểm dân cư O. Phải mở một con đường thẳng đi qua O như thế nào để theo con đường đó, hai đoạn đường từ điểm O đến con đường a và b bằng nhau (các con đường đều là đường thẳng) (H.3.27)?

 Xem đáp án
Xem đáp án
Sau bài học này ta giải quyết được bài toán như sau:
Gọi điểm giao nhau giữa hai đường thẳng a và b là điểm O
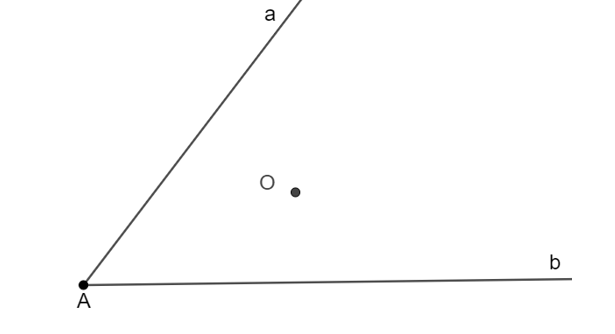
- Vẽ tia Ax đi qua điểm O. Trên tia Ax lấy điểm B sao cho OA = OB.
- Qua B vẽ tia By // Ab; Bz // Aa cắt hai tia Aa và Bb lần lượt tại hai điểm C và D
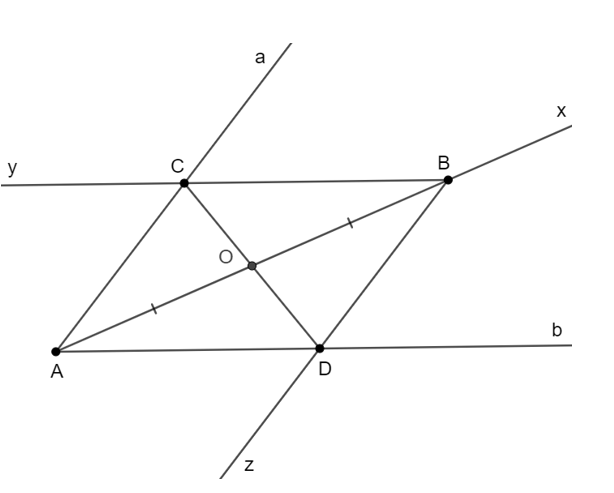
Khi đó, tứ giác ACBD là hình bình hành (vì AC // BD; AD // BC) có O là trung điểm AB nên O là trung điểm của CD.
Hai đoạn đường từ điểm O đến con đường a và b bằng nhau, tức là OC = OD.
Vậy con đường cần mở đường thẳng đi qua hai điểm C và D.
Câu 2:
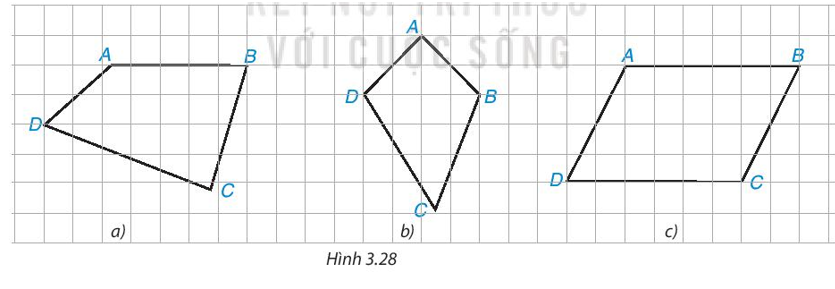
Trong Hình 3.28, có một hình bình hành. Đó là hình nào? Em có thể giải thích tại sao không?
 Xem đáp án
Xem đáp án
Tứ giác trong Hình 3.28c là hình bình hành vì:
Ta so sánh độ dài các cạnh đối trong tứ giác bằng cách đếm số ô vuông trong hình.
Ta thấy AB = CD; AD = BC.
Câu 3:
Vẽ hình bình hành, biết hai cạnh liên tiếp bằng 3 cm, 4 cm và góc xen giữa hai cạnh đó bằng 60o. Hãy mô tả cách vẽ và giải thích tại sao hình vẽ được là hình bình hành.
 Xem đáp án
Xem đáp án
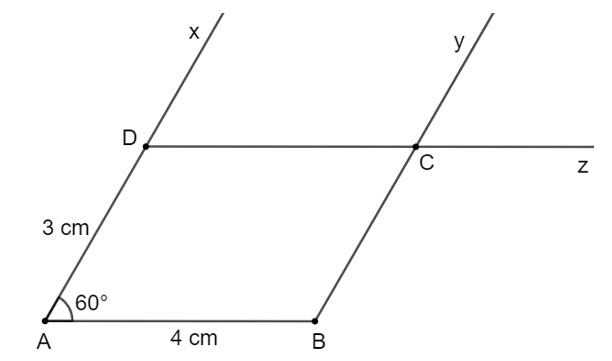
Giả sử hình bình hành ABCD có AD = 3cm, AB = 4 cm và .
Cách vẽ:
- Vẽ cạnh AB = 4 cm.
- Vẽ . Trên tia Ax lấy điểm D sao cho AD = 3cm.
- Kẻ By // AD, Dz // BC. Hai tia By và Dz cắt nhau tại C, ta được hình bình hành ABCD.
Hình vẽ được là hình bình hành vì có hai cặp cạnh đối song song (AB // CD, AD // BC).
Câu 4:
Hãy nêu các tính chất của hình bình hành mà em đã biết.
 Xem đáp án
Xem đáp án
Các tính chất của hình bình hành mà em đã biết:
- Hai cặp cạnh đối song song.
- Hai cặp cạnh đối bằng nhau.
Câu 5:
Cho hình bình hành ABCD (H.3.30).
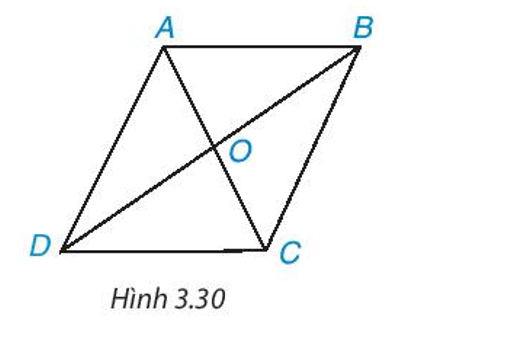
a) Chứng minh ∆ABC = ∆CDA.
Từ đó suy ra AB = CD, AD = BC và .
 Xem đáp án
Xem đáp án
a) Vì ABCD là hình bình hành nên AB // CD; AD // BC.
Suy ra (hai góc so le trong).
Xét ∆ABC và ∆CDA có:
(chứng minh trên);
Cạnh AC chung.
(chứng minh trên);
Do đó ∆ABC = ∆CDA (g.c.g).
Suy ra AB = CD, AD = BC (các cặp cạnh tương ứng); (hai góc tương ứng).
Câu 6:
b) Chứng minh ∆ABD = ∆CDB. Từ đó suy ra .
 Xem đáp án
Xem đáp án
b) Xét ∆ABD và ∆CDB có:
AB = CD (chứng minh trên);
AD = BC (chứng minh trên);
Cạnh BD chung.
Do đó ∆ABD = ∆CDB.
Suy ra (hai góc tương ứng).
Câu 7:
c) Gọi giao điểm của hai đường chéo AC, BD là O. Chứng minh ∆AOB = ∆COD. Từ đó suy ra OA = OC, OB = OD.
 Xem đáp án
Xem đáp án
c) Xét ∆AOB và ∆COD có:
(chứng minh trên);
AB = CD (chứng minh trên);
(chứng minh trên);
Do đó ∆AOB = ∆COD (g.c.g).
Suy ra OA = OC, OB = OD (các cặp cạnh tương ứng).
Câu 8:
Cho tam giác ABC. Từ một điểm M tùy ý trên cạnh BC, kẻ đường thẳng song song với AB, cắt cạnh AC tại N và kẻ đường thẳng song song với AC, cắt AB tại P. Gọi I là trung điểm của đoạn NP. Chứng minh rằng I cũng là trung điểm của đoạn thẳng AM.
 Xem đáp án
Xem đáp án
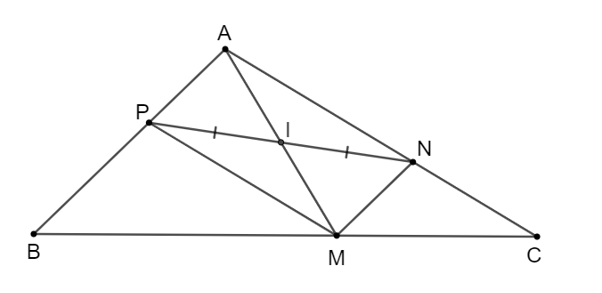
• MN // AP (vì MN // AB)
• MP // AN (vì MP // AC)
Do đó tứ giác APMN là hình bình hành.
Hình bình hành APMN có I là trung điểm của đoạn AP.
Do đó I là trung điểm của đoạn thẳng AM (đpcm).
Câu 9:
Tròn khẳng định: Hình thang cân có hai cạnh bên bằng nhau. Ngược lại, hình thang có hai cạnh bên bằng nhau thì nó là hình thang cân.
Vuông lại cho rằng: Tròn sai rồi!
Có trường hợp hình thang có hai cạnh bên bằng nhau nhưng nó lại là hình bình hành mà không phải là hình thang cân.
Theo em, bạn nào đúng? Vì sao?
 Xem đáp án
Xem đáp án
Khẳng định của bạn Vuông là đúng.
Trường hợp 1: Hình thang có hai cạnh bên bằng nhau nhưng không song song với nhau thì hình thang đó là hình thang cân.
Hình minh họa:

Trường hợp 2: Hình thang có hai cạnh bên bằng nhau và song song với nhau thì hình thang đó là hình bình hành.
Hình minh họa:

Câu 10:
Tròn khẳng định: Hình thang cân có hai cạnh bên bằng nhau. Ngược lại, hình thang có hai cạnh bên bằng nhau thì nó là hình thang cân.
Vuông lại cho rằng: Tròn sai rồi!
Có trường hợp hình thang có hai cạnh bên bằng nhau nhưng nó lại là hình bình hành mà không phải là hình thang cân.
Theo em, bạn nào đúng? Vì sao?
 Xem đáp án
Xem đáp án
Khẳng định của bạn Vuông là đúng.
Trường hợp 1: Hình thang có hai cạnh bên bằng nhau nhưng không song song với nhau thì hình thang đó là hình thang cân.
Hình minh họa:

Trường hợp 2: Hình thang có hai cạnh bên bằng nhau và song song với nhau thì hình thang đó là hình bình hành.
Hình minh họa:

Câu 11:
Hãy viết giả thiết, kết luận của Định lí 2.
 Xem đáp án
Xem đáp án
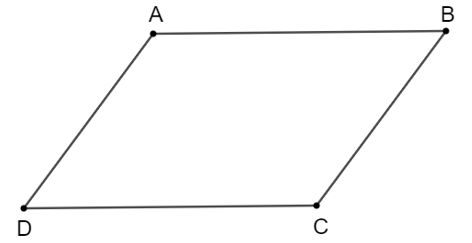
Giả thiết, kết luận của Định lí 2:
a)
|
GT |
Tứ giác ABCD có AB = CD; AD = BC |
|
|
KL |
Tứ giác ABCD là hình bình hành |
|
b)
|
GT |
Tứ giác ABCD có AB = CD; AB // CD |
|
|
KL |
Tứ giác ABCD là hình bình hành |
|
Câu 12:
Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB tại E và tia phân giác của góc B cắt CD tại F (H.3.32).
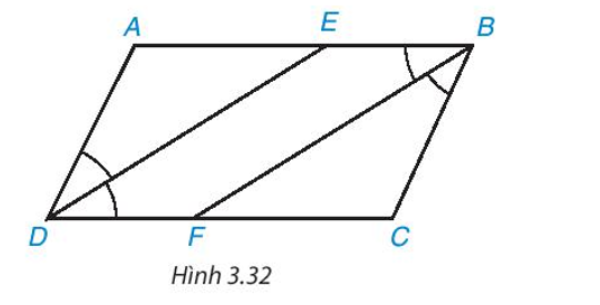
a) Chứng minh hai tam giác ADE và CBF là những tam giác cân, bằng nhau.
 Xem đáp án
Xem đáp án
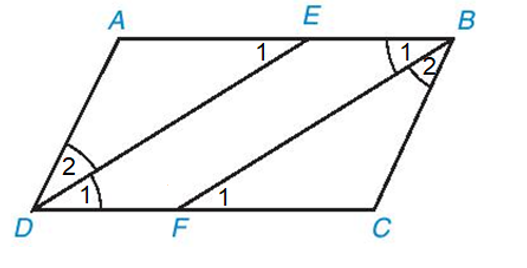
a) Vì ABCD là hình bình hành nên AB // CD hay BE // DF.
Vì DE là tia phân giác của nên .
Mà (BE // DF, hai góc so le trong) nên .
Suy ra tam giác ADE cân tại A.
Tương tự ta cũng chứng minh được: tam giác BCF cân tại C.
Vì ABCD là hình bình hành nên AD = BC; .
Vì AE là tia phân giác ; BF là tia phân giác nên
mà .
Do đó .
Xét ∆ADE và ∆CBF có:
(chứng minh trên);
AD = BC (chứng minh trên);
(chứng minh trên).
Do đó ∆ADE = ∆CBF (g.c.g).
Câu 13:
b) Tứ giác DEBF là hình gì? Tại sao?
 Xem đáp án
Xem đáp án
b) Vì mà (vì tam giác BCF cân tại C)
Suy ra (hai góc đồng vị).
Do đó DE // BF.
Tứ giác BEDF có:
BE // DF (chứng minh trên);
DE // BF (chứng minh trên).
Do đó, tứ giác BEDF là hình bình hành.
Câu 14:
Chia một sợi dây xích thành bốn đoạn: hai đoạn dài bằng nhau, hai đoạn ngắn bằng nhau và đoạn dài, đoạn ngắn xen kẽ nhau. Hỏi khi móc hai đầu mút của sợi dây xích đó lại để được một tứ giác ABCD (có các đỉnh tại các điểm chia) như Hình 3.33 thì tứ giác ABCD là hình gì? Tại sao?
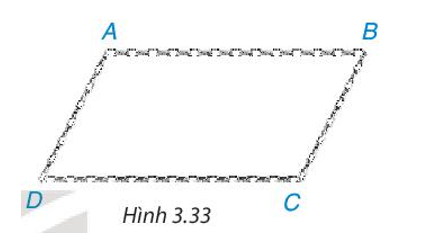
 Xem đáp án
Xem đáp án
Đoạn dây xích được chia thành:
• Hai đoạn dài có độ dài bằng nhau, tức là AB = CD;
• Hai đoạn ngắn có độ dài bằng nhau, tức là AD = BC.
Tứ giác ABCD có AB = CD; AD = BC nên tứ giác ABCD là hình bình hành.
Câu 15:
Hãy biết giả thiết, kết luận của Định lí 3.
 Xem đáp án
Xem đáp án
Giả thiết, kết luận của Định lí 3:
a)
|
GT |
Tứ giác ABCD có |
|
|
KL |
Tứ giác ABCD là hình bình hành |
|
b)
|
GT |
Tứ giác ABCD có AC cắt BD tại điểm O; OA = OC; OB = OD. |
|
|
KL |
Tứ giác ABCD là hình bình hành |
|
Câu 16:
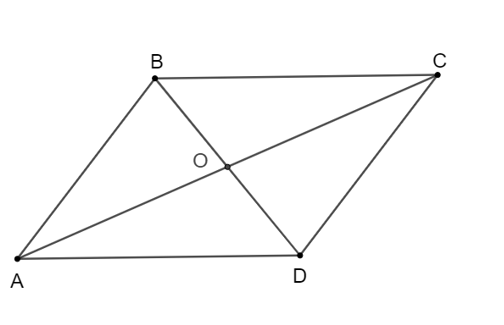
Cho hai điểm A, B phân biệt và điểm O không nằm trên đường thẳng AB. Gọi A’, B’ là các điểm sao cho O là trung điểm của AA’, BB’. Chứng minh rằng A’B’ = AB và đường thẳng A’B’ song song với đường thẳng AB.
 Xem đáp án
Xem đáp án
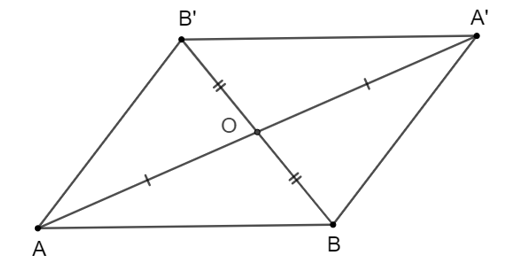
Ta hai điểm A, B phân biệt và điểm O không nằm trên đường thẳng AB.
Mà O là trung điểm của AA’, BB’ nên O là trung điểm của hai đường chéo của tứ giác ABA’B’.
Do đó tứ giác ABA’B’ là hình bình hành.
Câu 17:
Trở lại bài toán mở đầu. Em hãy vẽ hình và nêu cách vẽ con đường cần mở đi qua O sao cho theo con đường đó, hai đoạn đường từ O tới a và tới b bằng nhau.
 Xem đáp án
Xem đáp án
Gọi điểm giao nhau giữa hai đường thẳng a và b là điểm O
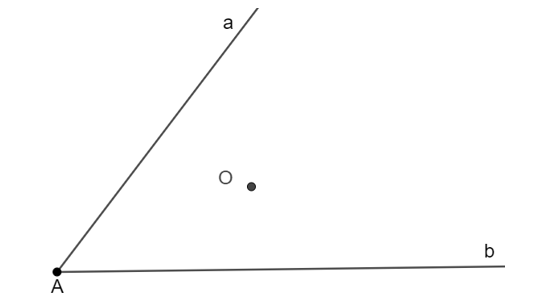
- Vẽ tia Ax đi qua điểm O. Trên tia Ax lấy điểm B sao cho OA = OB.
- Qua B vẽ tia By // Ab; Bz // Aa cắt hai tia Aa và Bb lần lượt tại hai điểm C và D.
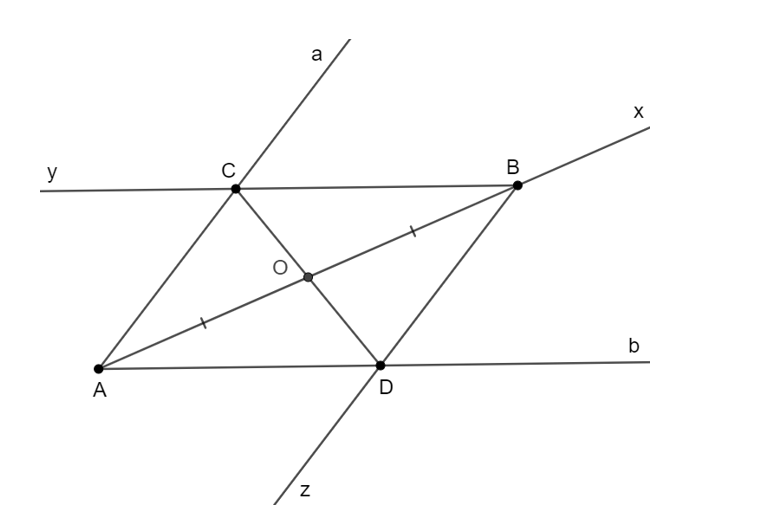
Khi đó, tứ giác ACBD là hình bình hành (vì AC // BD; AD // BC) có O là trung điểm AB nên O là trung điểm của CD.
Hai đoạn đường từ điểm O đến con đường a và b bằng nhau, tức là OC = OD.
Vậy con đường cần mở đường thẳng đi qua hai điểm C và D.
Câu 18:
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai? Vì sao?
a) Hình thang có hai cạnh bên song song là hình bình hành.
 Xem đáp án
Xem đáp án
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai? Vì sao?
a) Hình thang có hai cạnh bên song song là hình bình hành.
Câu 19:
b) Hình thang có hai cạnh bên bằng nhau là hình bình hành.
 Xem đáp án
Xem đáp án
b) Hình thang có hai cạnh bên bằng nhau là hình thang cân hoặc hình bình hành.
Vậy khẳng định b) sai.
Câu 20:
c) Tứ giác có hai cạnh đối nào cũng song song là hình bình hành.
 Xem đáp án
Xem đáp án
c) Tứ giác có hai cạnh đối nào cũng song song hay có hai cặp cạnh đối song song nên
tứ giác đó là hình bình hành.
Vậy khẳng định c) đúng.
Câu 22:
Cho hình bình hành ABCD. Gọi E, F lần lượt là trung điểm của AB, CD. Chứng minh BF = DE.
 Xem đáp án
Xem đáp án

Vì ABCD là hình bình hành nên AB = CD, AB // CD.
Mà E, F lần lượt là trung điểm của AB, CD nên AE = BE, CF = DF.
Do đó AE = BE = CF = DF.
Xét tứ giác BEDF có:
BE = DF (chứng minh trên);
BE // DF (vì AB // CD)
Do đó tứ giác BEDF là hình bình hành.
Suy ra BF = DE (đpcm).
Câu 23:
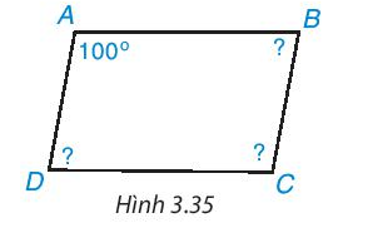
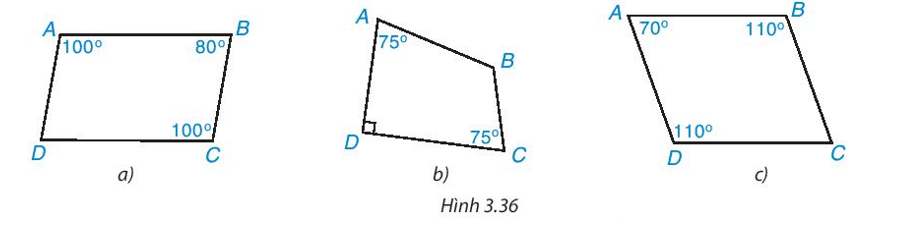
Trong mỗi trường hợp sau đây, tứ giác nào là hình bình hành, tứ giác nào không là hình bình hành? Vì sao?
 Xem đáp án
Xem đáp án
* Hình 3.36a)
Xét tứ giác ABCD có: .
Suy ra .
Tứ giác ABCD có: ; .
Do đó, tứ giác ABCD là hình bình hành.
* Hình 3.36b)
Xét tứ giác ABCD có: .
Suy ra .
Tứ giác ABCD có: nhưng .
Do đó, tứ giác ABCD không là hình bình hành.
* Hình 3.36c)
Xét tứ giác ABCD có: .
Suy ra .
Tứ giác ABCD có: ; .
Do đó, tứ giác ABCD là hình bình hành.
Vậy tứ giác ABCD trong Hình 3.36a) và 3.36c) là hình bình hành; tứ giác ABCD trong Hình 3.36b) không là hình bình hành.
Câu 24:
Cho hình bình hành ABCD. Gọi E, F lần lượt là trung điểm của các cạnh AB, CD. Chứng minh rằng:
a) Hai tứ giác AEFD, AECF là những hình bình hành;
 Xem đáp án
Xem đáp án
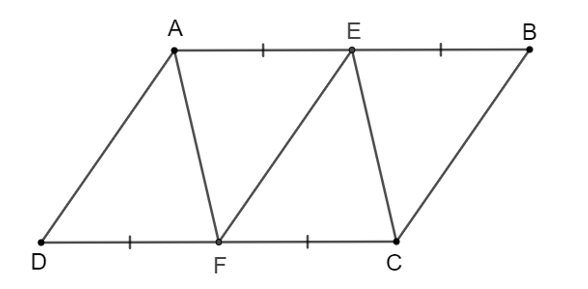
a) Vì ABCD là hình bình hành nên AB = CD, AB // CD.
Mà E, F lần lượt là trung điểm của AB, CD nên AE = BE, CF = DF.
Do đó AE = BE = CF = DF.
• Xét tứ giác AEFD có:
AE // DF (vì AB // CD);
AE = DF (chứng minh trên)
Do đó tứ giác AEFD là hình bình hành.
• Xét tứ giác AECF có:
AE // CF (vì AB // CD);
AE = CF (chứng minh trên)
Do đó tứ giác AECF là hình bình hành.
Vậy hai tứ giác AEFD, AECF là những hình bình hành.
Câu 25:
b) EF = AD, AF = EC.
 Xem đáp án
Xem đáp án
b) Vì tứ giác AEFD là hình bình hành nên EF = AD.
Vì tứ giác AECF là hình bình hành nên AF = EC.
Vậy EF = AD, AF = EC.
Câu 26:
Gọi O là giao điểm của hai đường chéo của hình bình hành ABCD. Một đường thẳng đi qua O lần lượt cắt các cạnh AB, CD của hình bình hành tại hai điểm M, N. Chứng minh ∆OAM = ∆OCN. Từ đó suy ra tứ giác MBND là hình bình hành.
 Xem đáp án
Xem đáp án
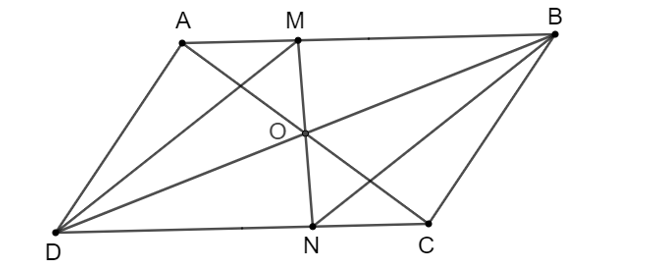
Vì ABCD là hình bình hành nên ta có:
• Hai đường chéo AC và BD cắt nhau tại O nên OA = OC, OB = OD.
• AB // CD nên AM // CN suy ra (hai góc so le trong).
Xét ∆OAM và ∆OCN có:
(chứng minh trên)
OA = OC (chứng minh trên)
(hai góc đối đỉnh)
Do đó ∆OAM = ∆OCN (g.c.g).
Suy ra AM = CN (hai cạnh tương ứng)
Mặt khác, AB = CD (chứng minh trên); AB = AM + BM; CD = CN + DN.
Suy ra BM = DN.
Xét tứ giác MBND có:
• BM // DN (vì AB // CD)
• BM = DN (chứng minh trên)
Do đó, tứ giác MBND là hình bình hành.