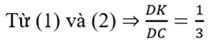Trắc nghiệm chuyên đề Toán 8 Chủ đề 13: Ôn tập và kiểm tra có đáp án (Đề 3)
-
828 lượt thi
-
11 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 2:
Xem đáp án
Chọn đáp án A
Câu 5:
Xem đáp án
Chọn đáp án C
Câu 6:
Xem đáp án
Chọn đáp án B
Câu 7:
Cho hình thoi ABCD có O là giao điểm hai đường chéo. Gọi I là trung điểm cạnh BC và E là điểm đối xứng với O qua I.
a) Tứ giác OBEC là hình gì? Tại sao?
Xem đáp án
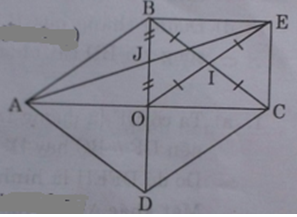
a) Ta có IB = IC (gt), IO = IE (tính chất đối xứng)
⇒ OBEC là hình bình hành.
Lại có ∠BOC = 90o (tính chất hai đường chéo hình thoi).
Do đó OBEC là hình chữ nhật.
Câu 8:
b) Chứng tỏ E đối xứng với A qua trung điểm J của đoạn O B.
Xem đáp án
b)Ta có OA = OC (tính chất đường chéo hình thoi)
Mà OC = BE và OC // BE (cmt) nên OA = BE và OA // BE.
Do đó ABEO là hình bình hành
Ta có J là trung điểm của OB nên đường chéo thứ hai AI phải qua J và JA = JE.
⇒ E đối xứng với A qua trung điểm J của đoạn OB.
Câu 9:
Cho tam giác ABC vuông tại A ( AB < AC). Gọi I là trung điểm của BC. Qua I vẽ IM ⊥ AB tại M, và IN ⊥ AC tại N.
a) Chứng minh AMIN là hình chữ nhật.
Xem đáp án
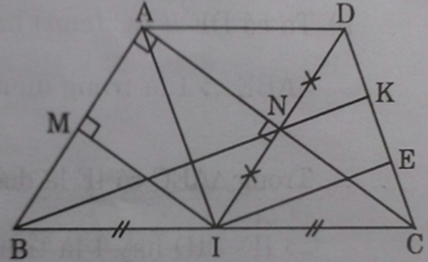
a) Xét tứ giác ANIM có:
(AMI) = 90o
(ANI) = 90o
(MAN) = 90o
⇒ Tứ giác ANIM là hình chữ nhật (có ba góc vuông)
Câu 10:
b) Gọi D là điểm đối xứng của I qua N. Chứng minh ADCI là hình thoi.
Xem đáp án
b) I là trung điểm của BC nên AI là đường trung tuyến của tam giác vuông ABC
⇒ AI = IC = . (1)
Do đó ΔAIC cân có IN là đường cao nên đồng thời là trung tuyến hay NA = NC (2)
lại có NI = NI (tính chất đối xứng) (3)
Từ (1), (2), (3) ⇒ ADIC là hình thoi.
Câu 11:
c) Đường thẳng BN cắt DC tại K. Chứng minh:
Xem đáp án
c) Kẻ qua I đường thẳng song song với BK cắt CD tai E.
Ta có: I là trung điểm của BC; IE // BK
⇒ E là trung điểm của CK hay EK = EC (1)
Mặt khác N là trung điểm của ID và NK // IE ( IE // BK)
⇒ K là trung điểm của DE hay EK = DK (2)
