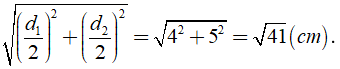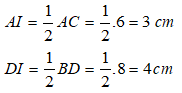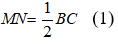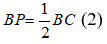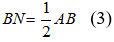Trắc nghiệm Hình thoi (có đáp án)
-
657 lượt thi
-
10 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Khoanh tròn vào phương án đúng trong các phương án sau ?
Xem đáp án
Định nghĩa: Hình thoi là tứ giác có bốn cạnh bằng nhau.
Chọn đáp án D.
Câu 2:
Trong các khẳng định sau, khẳng định nào sai về hình thoi ?
Xem đáp án
Định lí: Trong hình thoi:
+ Hai đường chéo vuông góc với nhau.
+ Hai đường chéo là các đường phân giác các góc của hình thoi.
+ Hai đường chéo cắt nhau tại trung điểm mỗi đường.
⇒ Đáp án A sai.
Chọn đáp án A.
Câu 3:
Hai đường chéo của hình thoi có độ dài lần lượt là 8cm và 10cm. Độ dài cạnh của hình thoi đó là ?
Xem đáp án
Vì hình thoi có hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm mỗi đường
→ Độ dài đường chéo của hình thoi là:
Chọn đáp án B.
Câu 4:
Hình thoi có độ dài các cạnh là 4cm thì chu vi là hình thoi là?
Xem đáp án
Chu vi của hình thoi là
Chọn đáp án C.
Câu 5:
Các phương án sau, phương án nào sai?
Xem đáp án
Định lí:
+ Hình thoi có hai trục đối xứng là hai đường chéo của hình thoi.
+ Có một tâm đối xứng là giao điểm của hai đường chéo.
Mở rộng:
+ Trong hình chữ nhật, các trung điểm của các cạnh hình chữ nhật là các đỉnh của một hình thoi.
+ Trong hình thoi, các trung điểm của bốn cạnh hình thoi là các hình chữ nhật.
→ Đáp án D sai.
Chọn đáp án D.
Câu 6:
Cho hình bình hành ABCD có I là giao điểm hai đường chéo. Biết rằng AC = 6cm và BD = 8cm và AD = 5cm. Tìm khẳng định sai ?
Xem đáp án
Theo tính chất hình bình hành ta có: I là trung điểm của AC và BD.
Suy ra:
Xét tam giác AID có:
Suy ra: tam giác AID là tam giác vuông: AI ⊥ DI hay AC ⊥ BD
Hình bình hành ABCD có 2 đường chéo AC và BD vuông góc với nhau nên là hình thoi.
Suy ra: AB = BC = CD = DA = 5cm
Chọn đáp án B
Câu 7:
Cho hình thoi ABCD có O là giao điểm hai đường chéo, biết AC = 16cm và OB = 6cm. Tính CD?
Xem đáp án
Do ABCD là hình thoi nên: AO = OC = 1/2 AC = 8cm
Áp dụng định lí Pytago vào tam giác vuông ABO ta có:
nên AB = 10cm
Vì ABCD là hình thoi nên AB = CD = 10cm
Chọn đáp án D
Câu 8:
Cho tam giác ABC , gọi M, N và P lần lượt là trung điểm của AC; AB và BC. biết AB = BC. Hỏi tứ giác NMPB là hình gì?
Xem đáp án
* Xét tam giác ABC có M và N lần lượt là trung điểm của AC và AB nên MN là đường trung bình của tam giác ABC.
Suy ra: MN// BC và 
* Lại có: P là trung điểm của BC nên 
Từ (1) và (2) suy ra: MN = BP.
Tứ giác NMPB có 2 cạnh đối MN và BP song song và bằng nhau nên là hình bình hành.
* Lại có: N là trung điểm của AB nên
Theo giả thiết AB = BC nên từ (2) và (3) suy ra: BP = BN
Hình bình hành NMPB có 2 cạnh kề BP và BN bằng nhau nên là hình thoi.
Chọn đáp án A
Câu 9:
Cho tam giác ABC cân tại A có AM là đường trung tuyến. Điểm D đối xứng với điểm A qua M. Hỏi tứ giác ABDC là hình gì?
Xem đáp án
Do tam giác ABC cân tại A có AM là đường trung tuyến nên đồng thời là đường cao:
AM ⊥ BC và M là trung điểm của BC.
Do D đối xứng vơi A qua M nên M là trung điểm của AD.
Tứ giác ABDC có hai đường chéo cắt nhau tại trung điểm mỗi đường nên là hình bình hành.
Lại có: AD ⊥ BC nên tứ giác ABDC là hình thoi.
Chọn đáp án C
Câu 10:
Cho hình thoi ABCD có CD = 4cm và . Tính AC
Xem đáp án
Do ABCD là hình thoi nên BD là đường phân giác của góc
Suy ra:
Xét tam giác ABC có AB = BC ( vì ABCD là hình thoi) và
Suy ra: tam giác ABC là tam giác đều.
Vì ABCD là hình thoi nên AB = BC = CD = DA =4cm
Suy ra : AC = AB = BC = 4cm.
Chọn đáp án D