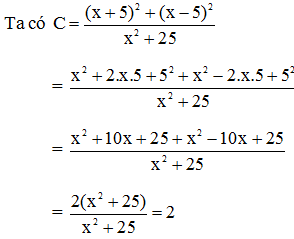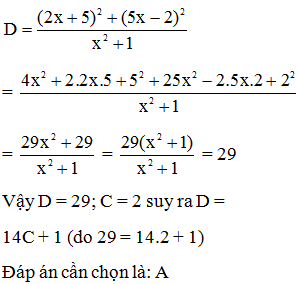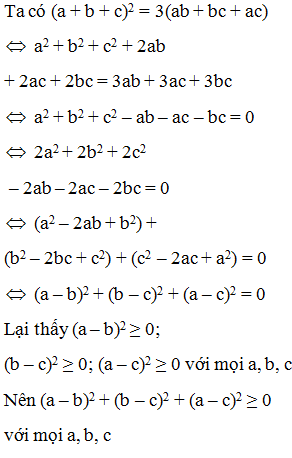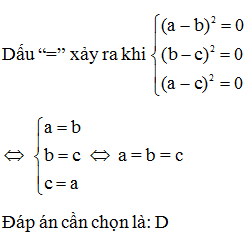18 câu hỏi trắc nghiệm thuộc Trắc nghiệm những hằng đẳng thức đáng nhớ (Vận dụng)

Câu 1:

Cho $C = \frac{{(x + 5)}^{2} + {(x - 5)}^{2}}{x^{2} + 25}$ và $D = \frac{{(2 x + 5)}^{2} + {(5 x - 2)}^{2}}{x^{2} + 1}$ . Tìm mối quan hệ giữa C và D.

A. D = 14C + 1

B. D = 14C

C. D = 14C – 1

D. D = 14C – 2

Xem đáp án

Câu 2:

So sánh A = 2016.2018.a và B = 2017².a (với a > 0)

A. A = B

B. A < B

C. A > B

D. A ≥ B

Xem đáp án

Ta có A = 2016.2018.a = (2017 – 1)(2017 + 1)a = (2017² – 1)a

Vì 2017² – 1 < 2017² và a > 0 nên (2017² – 1)a < 2017²a hay A < B

Đáp án cần chọn là: B

Câu 3:

So sánh A = 2019.2021.a và B = (2019² + 2.2019 + 1)a (với a > 0)

A. A= B

B. A ≥ B

C. A > B

D.A < B

Xem đáp án

Ta có A = 2019.2021.a = (2020 – 1)(2020 + 1)a = (2020² – 1)a

Và B = (2019² + 2.2019 + 1)a = (2019 + 1)²a = 2020²a

Vì 2020² – 1 < 2020² và a > 0 nên (2020² – 1)a < 2020²a hay A < B

Đáp án cần chọn là: D

Câu 4:

So sánh M = 2³² và N = (2 + 1)(2² + 1)(2⁴ + 1)(2⁸ + 1)(2¹⁶ + 1)

A. M > N

B. M < N

C. M = N

D. M = N – 1

Xem đáp án

Ta có N = (2 + 1)(2² + 1)(2⁴ + 1)(2⁸ + 1)(2¹⁶ + 1)

2² - 1 = 4 - 1 = 3 = 2 + 1

Suy ra N = [(2² – 1)(2² + 1)](2⁴ + 1)(2⁸ + 1)(2¹⁶ + 1)

= (2⁴ – 1)(2⁴ + 1)(2⁸ + 1)(2¹⁶ + 1)

= (2⁸ – 1)(2⁸ + 1)(2¹⁶ + 1)

= (2¹⁶ - 1)(2¹⁶ + 1) = (2¹⁶)² – 1 = 2³² – 1

Mà 2³² – 1 < 2³² => N < M hay M > N

Đáp án cần chọn là: A

Câu 5:

Chọn câu đúng về giá trị các biểu thức sau mà không tính cụ thể

A = 1 + 15(4² + 1)(4⁴ + 1)(4⁸ + 1) và B = (4³)⁵ + (4⁵)³

A. A = B + 2

B. B = 2A

C. A = 2B

D. A = B

Xem đáp án

Ta có A = 1 + 15(4² + 1)(4⁴ + 1)(4⁸ + 1)

= 1 + (4² – 1)(4² + 1)(4⁴ + 1)(4⁸ + 1)

= 1 + [(4²)² – 1](4⁴ + 1)(4⁸ + 1)

= 1 + (4⁴ – 1)(4⁴ + 1)(4⁸+ 1) = 1 + [(4⁴)² – 1](4⁸ + 1)

= 1 + (4⁸ – 1)(4⁸ + 1) = 1 + (4⁸)² – 1 = 1 + 4¹⁶ – 1 = 4¹⁶

= 4.4¹⁵

Và B = (4³)⁵ + (4⁵)³ = 4^3.5 + 4^5.3 = 4¹⁵ + 4¹⁵ = 2.4¹⁵

Vì A = 4.4¹⁵; B = 2.4¹⁵ => A = 2B

Đáp án cần chọn là: C

Câu 6:

Cho P = -4x² + 4x – 2. Chọn khẳng định đúng

A. P ≤ -1

B. P > -1

C. P > 0

D. P ≤ - 2

Xem đáp án

Ta có P = -4x² + 4x – 2

= -4x² + 4x – 1 – 1 = -(4x² – 4x + 1) – 1

= -1 – (2x – 1)²

Nhận thấy –(2x – 1)² ≤ 0

=> -1 – (2x – 1)² ≤ -1, Ɐx hay P ≤ -1.

Đáp án cần chọn là: A

Câu 7:

Cho T = -9x² + 6x – 5. Chọn khẳng định đúng

A. T < -4

B. T ≥ -4

C. T > -4

D.T ≤ -4

Xem đáp án

Ta có T = -9x² + 6x – 5 = -9x² + 6x – 1 – 4

= -4 – (9x² – 6x + 1) = -4 – (3x – 1)²

Nhận thấy –(3x – 1)² ≤ 0 => -4 – (3x – 1)² ≤ -4, Ɐx hay T ≤ -4

Đáp án cần chọn là: D

Câu 8:

Tìm giá trị lớn nhất của biểu thức Q = 8 – 8x – x²

A. 8

B. 11

C. -4

D. 24

Xem đáp án

Ta có Q = 8 – 8x – x²

= -x² – 8x – 16 + 16 + 8 = -(x + 4)² + 24

= 24 – (x + 4)²

Nhận thấy (x + 4)² ≥ 0; Ɐx

=> 24 – (x + 4)² ≤ 24

Dấu “=” xảy ra khi (x + 4)² = 0 x = -4

Giá trị lớn nhất của Q là 24 khi x = -4

Đáp án cần chọn là: D

Câu 9:

Tìm giá trị lớn nhất của biểu thức B = 4 – 16x² – 8x

A.5

B. -5

C. 8

D. $- \frac{1}{4}$

Xem đáp án

Ta có B = 4 – 16x² – 8x

= 5 – (16x² + 8x + 1) = 5 – [(4x)² + 2.4x.1 + 1²]

= 5 – (4x + 1)²

Nhận thấy (4x + 1)² ≥ 0; Ɐx

=> 5 – (4x + 1)²≤ 5

Dấu “=” xảy ra khi (4x + 1)² = 0 x = $- \frac{1}{4}$

Đáp án cần chọn là: A

Câu 10:

Biểu thức E = x² – 20x +101 đạt giá trị nhỏ nhất khi

A. 9

B. 10

C. 11

D. 12

Xem đáp án

Ta có E = x² – 20x +101 = x² – 2.x.10 + 100 + 1 = (x – 10)² + 1

Vì (x – 10)² ≥ 0; Ɐx => (x – 10)² + 1 ≥ 1

Dấu “=” xảy ra khi (x – 10)² = 0 x – 10 = 0 x = 10

Vậy giá trị nhỏ nhất của E là 1 khi x = 10

Đáp án cần chọn là: B

Câu 11:

Biểu thức F = x² – 12x +34 đạt giá trị nhỏ nhất khi

A. 6

B. -6

C. 8

D.2

Xem đáp án

Ta có

F = x² – 12x +34 = x² – 2.x.6 + 6² – 2 = (x – 6)² – 2

Vì (x – 6)² ≥ 0; Ɐx => (x – 6)² – 2 ≥ - 2

Dấu “=” xảy ra khi (x – 6)² = 0 x – 6 = 0 x = 6

Vậy giá trị nhỏ nhất của E là -2 khi x = 6

Đáp án cần chọn là: A

Câu 12:

Biểu thức K = x² – 6x + y² – 4y + 6 có giá trị nhỏ nhất là

A. 6

B. 1

C. -7

D. 7

Xem đáp án

Ta có K = x² – 6x + y² – 4y + 6

= x² – 2x.3 + 9 + y² – 2.y.2 + 4 – 7

= (x – 3)² + (y – 2)² – 7

Vì (x – 3)² ≥ 0; (y – 2)² ≥ 0; Ɐx; y nên (x – 3)² + (y – 2)² – 7 ≥ -7

Dấu “=” xảy ra khi $\{\begin{cases} x - 3 = 0 \\ y - 2 = 0 \end{cases}$ <=> $\{\begin{cases} x = 3 \\ y = 2 \end{cases}$

Vậy giá trị nhỏ nhất của K là -7 khi x = 3; y = 2

Đáp án cần chọn là: C

Câu 13:

Biểu thức J = x² – 8x + y² + 2y+ 5 có giá trị nhỏ nhất là

A. -12

B. 5

C. 12

D. -5

Xem đáp án

Ta có J = x² – 8x + y² + 2y+ 5

= x² – 2.x.4 + 16 + y² + 2.y.1 + 1 – 12

= (x – 2)² + (y + 1)² – 12

Vì (x – 2)² ≥ 0; (y + 1)² ≥ 0; Ɐx; y nên (x – 2)² + (y + 1)² – 12 ≥ -12

Dấu “=” xảy ra khi $\{\begin{cases} x - 2 = 0 \\ y + 1 = 0 \end{cases}$ <=> $\{\begin{cases} x = 2 \\ y = - 1 \end{cases}$

Vậy giá trị nhỏ nhất của J là -12 khi x = 2; y = -1

Đáp án cần chọn là: A

Câu 14:

Giá trị nhỏ nhất của biểu thức I = (x² + 4x + 5)(x² + 4x + 6) + 3 là

A. 4

B. 5

C. 3

D. 2

Xem đáp án

Ta có I = (x² + 4x + 5)(x² + 4x + 6) + 3

= (x² + 4x + 5)(x² + 4x + 5 + 1) + 3

= (x² + 4x + 5)² + (x² + 4x + 5) + 3

= (x² + 4x + 5)² + (x² + 4x + 4) + 4

= (x² + 4x + 5)² + (x + 2)² + 4

Ta có x² + 4x + 5 = x² + 4x + 4 + 1

= (x + 2)² + 1 ≥ 1; Ɐx nên (x² + 4x + 5)² ≥ 1; Ɐx

Và (x + 2)² ≥ 0; Ɐx (x² + 4x + 5)² + (x + 2)² + 4 ≥ 1 + 4

(x² + 4x + 5)² + (x + 2)² + 4 ≥ 5

Dấu “=” xảy ra khi $\{\begin{cases} x^{2} + 4 x + 5 = 1 \\ {(x + 2)}^{2} = 0 \end{cases}$ => x = -2

Vậy giá trị nhỏ nhất của I là 5 khi x = -2

Đáp án cần chọn là: B

Câu 15:

Giá trị nhỏ nhất của biểu thức K = (x² + 2x + 3)(x² + 2x + 4) là

A. 6

B. 2

C. 4

D. 3

Xem đáp án

Ta có K = (x² + 2x + 3)(x² + 2x + 4)

= (x² + 2x + 3) (x² + 2x + 3 + 1)

= (x² + 2x + 3)² + (x² + 2x + 3)

= (x² + 2x + 3)² + (x² + 2x + 1) + 2

= (x² + 2x + 3)² + (x + 1)² + 2

Ta có x² + 2x + 3 = x² + 2x + 1 + 2 = (x + 1)² + 2 ≥ 2; Ɐx

Nên (x² + 2x + 3)² ≥ 4;

Và (x + 1)² ≥ 0; nên (x² + 2x + 3)² + (x + 1)² + 2 ≥ 4 + 2

(x² + 2x + 3)² + (x + 1)² + 2 ≥ 6

Dấu “=” xảy ra khi $\{\begin{cases} x^{2} + 2 x + 3 = 2 \\ {(x + 1)}^{2} = 0 \end{cases}$ => x = -1

Vậy giá trị nhỏ nhất của K là 6 khi x = -1

Đáp án cần chọn là: A

Câu 16:

Cho M = 77² + 75² + 73² + … + 3² + 1² và N = 76² + 74² + … + 2²

Tính giá trị của biểu thức $\frac{M - N - 3}{3000}$

A. 10

B. 30

C. 1

D. 100

Xem đáp án

Xét M – N = 77² + 75² + 73² + … + 3² + 1² – (76² + 74² + … + 2²)

= (77² – 76²) + (75² – 74²) + (73² – 72²) + … + (3² – 2²) + 1²

= (77 + 76)(77 – 76) + (75 + 74)(75 – 74) + … + (3 + 2)(3 – 2) + 1

= (77 + 76).1 + (75 + 74).1 + … + (3 + 2).1 + 1

= 77 + 76 + 75 + 74 + 73 + … + 3 + 2 + 1

= $\frac{77 + 1}{2} .77 = 3003$

Từ đó $\frac{M - N - 3}{3000} = \frac{3003 - 3}{3000} = \frac{3000}{3000} = 1$

Đáp án cần chọn là: C

Câu 17:

Cho (a + b + c)² = 3(ab + bc + ac). Khi đó

A. a = -b = -c

B. $a = b = \frac{c}{2}$

C. a = 2b = 3c

D. a = b = c

Xem đáp án

Câu 18:

Nhà bạn Minh và bạn An cùng trồng bắp cải trên hai mảnh vườn hình vuông khác nhau. Các cây bắp cải được cách đều nhau. Do vườn nhà bạn Minh lớn hơn nên số cây bắp cải trồng được lớn hơn vườn nhà bạn An là 211 cây. Hỏi nhà bạn Minh đã trồng bao nhiêu cây bắp cải?

A. 106 cây

B. 11025 cây

C. 11236 cây

D. 105 cây

Xem đáp án

Gọi số cây bắp cải trồng trên mỗi cạnh của vườn hình vuông nhà bạn Minh là y cây (y N^*)

Và số cây bắp cải trồng trên mỗi cạnh của vườn hình vuông nhà bạn An là x cây (x N^*)

Suy ra số cây bắp cải trồng được trên vườn nhà Minh là y² cây

Số cây bắp cải trồng trên vườn nhà An là x² cây

Theo bài ra ta có y² – x² = 211

(y – x)(y + x) = 211

Mà 211 là số nguyên tố và y – x < y + x nên ta có (y – x)(y + x) = 1.211 hay

Từ (1) suy ra y = x + 1, thay xuống (2) ta được x + 1 + x = 211

2x = 210 x = 105

Suy ra y = 105 + 1 = 105 + 1 = 106

Vậy số cây bắp cải vườn nhà bạn Minh trồng là 106² = 11236 cây

Đáp án cần chọn là: C

Gọi số cây bắp cải trồng trên mỗi cạnh của vườn hình vuông nhà bạn Minh là y cây (y N^*)

Và số cây bắp cải trồng trên mỗi cạnh của vườn hình vuông nhà bạn An là x cây (x N^*)

Suy ra số cây bắp cải trồng được trên vườn nhà Minh là y² cây

Số cây bắp cải trồng trên vườn nhà An là x² cây

Theo bài ra ta có y² – x² = 211

(y – x)(y + x) = 211

Mà 211 là số nguyên tố và y – x < y + x nên ta có (y – x)(y + x) = 1.211 hay

$\{\begin{cases} y - x = 1 (1) \\ y + x = 211 (2) \end{cases}$

Từ (1) suy ra y = x + 1, thay xuống (2) ta được x + 1 + x = 211

2x = 210 x = 105

Suy ra y = 105 + 1 = 105 + 1 = 106

Vậy số cây bắp cải vườn nhà bạn Minh trồng là 106² = 11236 cây

Đáp án cần chọn là: C

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Những hằng đẳng thức đáng nhớ có đáp án

Trắc nghiệm những hằng đẳng thức đáng nhớ (Vận dụng)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương