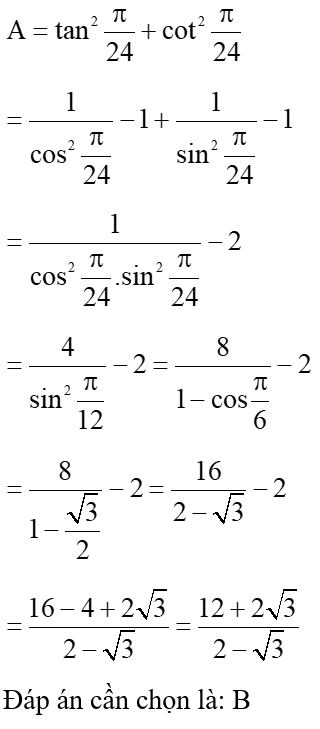14 câu hỏi trắc nghiệm thuộc Trắc nghiệm Ôn tập chương VI có đáp án

Câu 1:

Cho $\cot α = 3$ . Khi đó $\frac{3 \sin α - 2 \cos α}{12 \sin^{3} α + 4 \cos^{3} α}$ có giá trị bằng:

A $- \frac{1}{4}$ .

B. $- \frac{5}{4}$

C. $\frac{3}{4}$

D. $\frac{1}{4}$

Xem đáp án

Ta có:

$\cot α = 3 \Rightarrow \frac{\cos α}{\sin α} = 3 \Leftrightarrow \cos α = 3 \sin α$

Thay vào biểu thức đề bài, ta được:

$\frac{3 \sin α - 2.3 \sin α}{12 \sin^{3} α + 4 {(3 \sin α)}^{3}} = \frac{- 3 \sin α}{120 \sin^{3} α} = - \frac{1}{40} . \frac{1}{\sin^{2} α} = - \frac{1}{40} (1 + \cot^{2} α)$

$= - \frac{1}{40} (1 + 3^{2}) = - \frac{1}{4}$

Đáp án cần chọn là: A

Câu 2:

Tính $B = \frac{1 + 5 \cos α}{3 - 2 \cos α}$ biết $\tan \frac{α}{2} = 2$

A. $\frac{- 2}{21}$

B. $\frac{20}{9}$

C. $\frac{2}{21}$

D. $- \frac{10}{21}$

Xem đáp án

Ta có: $\tan^{2} \frac{α}{2} = \frac{\sin^{2} \frac{α}{2}}{\cos^{2} \frac{α}{2}} = \frac{\frac{1 - \cos α}{2}}{\frac{1 + \cos α}{2}} = \frac{1 - \cos α}{1 + \cos α}$

$\Leftrightarrow 1 - \cos α = \tan^{2} \frac{α}{2} (1 + \cos α)$

Đặt $\tan \frac{α}{2} = t$ thì $\cos α = \frac{1 - t^{2}}{1 + t^{2}}$

Với t = 2 $\Rightarrow \cos α = \frac{1 - 4}{1 + 4} = \frac{- 3}{5}$

Suy ra $B = \frac{1 + 5 (\frac{- 3}{5})}{3 - 2 (\frac{- 3}{5})} = \frac{- 2}{\frac{21}{5}} = \frac{- 10}{21}$

Đáp án cần chọn là: D

Câu 3:

Giá trị của biểu thức $A = \tan^{2} \frac{π}{24} + \cot^{2} \frac{π}{24}$ bằng:

A. $\frac{12 - 2 \sqrt{3}}{2 + \sqrt{3}}$

B. $\frac{12 + 2 \sqrt{3}}{2 - \sqrt{3}}$

C. $\frac{12 + 2 \sqrt{3}}{2 + \sqrt{3}}$

D. $\frac{12 - 2 \sqrt{3}}{2 - \sqrt{3}}$

Xem đáp án

Câu 4:

Cho $\sin a - \cos a = \frac{3}{4}$ . Tính sin2a

A. $\sin 2 a = \frac{- 5}{4}$

B. $\sin 2 a = \frac{7}{16}$

C. $\sin 2 a = \frac{- 7}{16}$

D. $\sin 2 a = \frac{5}{4}$

Xem đáp án

Câu 5:

Khẳng định nào sau đây đúng?

A. $\sin^{4} a - \cos^{4} a = \cos 2 a$

B. $2 (\sin^{4} a + \cos^{4} a) = 2 - \sin^{2} 2 a$

C. ${(\sin a - \cos a)}^{2} = 1 - 2 \sin 2 a$

D. ${(\sin^{2} a + \cos^{2} a)}^{3} = 1 + 2 \sin^{4} a . \cos^{4} a$

Xem đáp án

+ $\sin^{4} a - \cos^{4} a = (\sin^{2} a - \cos^{2} a) (\sin^{2} a + \cos^{2} a) = (\sin^{2} a - \cos^{2} a) .1 = - \cos 2 a$ nên A sai

+ $2 (\sin^{4} a + \cos^{4} a) = 2 [{(\sin^{2} a + \cos^{2} a)}^{2} - 2 \sin^{2} a . \cos^{2} a] = 2 (1 - 2. \frac{1}{4} \sin^{2} 2 a) = 2 - \sin^{2} 2 a$ nên B đúng

+ ${(\sin a - \cos a)}^{2} = 1 - 2 \sin a . \cos a = 1 - \sin 2 a$ nên C sai

+ ${(\sin^{2} a + \cos^{2} a)}^{3} = 1$ và $1 + 2 \sin^{4} a . \cos^{4} a = 1 + 2. {(\frac{1}{2} \sin 2 a)}^{4} = 1 + \frac{1}{8} \sin^{4} 2 a$ nên D sai

Đáp án cần chọn là: B

Câu 6:

Tính giá trị của $G = \cos^{2} \frac{π}{6} + \cos^{2} \frac{2 π}{6} + ... + \cos^{2} \frac{5 π}{6} + \cos^{2} π$

A. 3

B. 2

C. 0

D. 1

Xem đáp án

$G = \cos^{2} \frac{π}{6} + \cos^{2} \frac{2 π}{6} + ... + \cos^{2} \frac{5 π}{6} + \cos^{2} π$

$= (\cos^{2} \frac{π}{6} + \cos^{2} \frac{2 π}{6}) + (\cos^{2} \frac{4 π}{6} + \cos^{2} \frac{5 π}{6}) + (\cos^{2} \frac{π}{2} + \cos^{2} π)$

$= (\cos^{2} \frac{π}{6} + \cos^{2} \frac{π}{3}) + (\cos^{2} \frac{2 π}{6} + \cos^{2} \frac{π}{6}) + 1$

$= 2 (\cos^{2} \frac{π}{6} + \cos^{2} \frac{2 π}{6}) + 1$

$= 2 (\cos^{2} \frac{π}{6} + \cos^{2} \frac{π}{6}) + 1$ = 3

Đáp án cần chọn là: A

Câu 7:

Tính

A. 0

B. 1

C. -1

D. -2

Xem đáp án

$E = \sin \frac{π}{5} + \sin \frac{2 π}{5} + ... + \sin \frac{9 π}{5}$

$= (\sin \frac{π}{5} + \sin \frac{9 π}{5}) + (\sin \frac{2 π}{5} + \sin \frac{8 π}{5}) + ... + (\sin \frac{4 π}{5} + \sin \frac{6 π}{5}) + \sin \frac{5 π}{5}$

$= [\sin \frac{π}{5} + \sin (2 π - \frac{π}{5})] + [\sin \frac{2 π}{5} + \sin (2 π - \frac{2 π}{5})] + ... + [\sin \frac{4 π}{5} + \sin (2 π - \frac{4 π}{5})] + \sin π$

$= [\sin \frac{π}{5} + \sin (- \frac{π}{5})] + [\sin \frac{2 π}{5} + \sin (- \frac{2 π}{5})] + ... + [\sin \frac{4 π}{5} + \sin (- \frac{4 π}{5})] + 0$

$= (\sin \frac{π}{5} - \sin \frac{π}{5}) + (\sin \frac{2 π}{5} - \sin \frac{2 π}{5}) + ... + (\sin \frac{4 π}{5} - \sin \frac{4 π}{5})$

= 0 + 0 + … + 0 = 0

Đáp án cần chọn là: A

Câu 8:

Ta có $\sin^{8} x + \cos^{8} x = \frac{a}{64} + \frac{b}{16} \cos 4 x + \frac{c}{64} \cos 8 x$ với $a, b \in Q$ . Khi đó a – 5b + c bằng:

A. 1

B. 2

C. 3

D. 4

Xem đáp án

$\sin^{8} x + \cos^{8} x = {(\sin^{4} x + \cos^{4} x)}^{2} - 2 \sin^{4} x . \cos^{4} x$

= $(1 - 2 \sin^{2} x . \cos^{2} x) - \frac{1}{8} \sin^{4} 2 x$

= ${(1 - \frac{1}{2} \sin^{2} 2 x .)}^{2} - \frac{1}{8} \sin^{4} 2 x = 1 - \sin^{2} 2 x + \frac{1}{8} \sin^{4} 2 x$

= $1 - \frac{1 - \cos 4 x}{2} + \frac{1}{8} {(\frac{1 - \cos 4 x}{2})}^{2}$

= $1 - \frac{1 - \cos 4 x}{2} + \frac{1}{32} {(1 - 2 \cos 4 x + \frac{1 + \cos 8 x}{2})}^{2}$

= $\frac{35}{64} + \frac{7}{16} \cos 4 x + \frac{1}{64} \cos 8 x$

$\Rightarrow a = 35, b = 7, c = 1 \Rightarrow a - 5 b + c = 1$

Đáp án cần chọn là: A

Câu 9:

Nếu $α$ là góc nhọn và $\sin \frac{α}{2} = \sqrt{\frac{x - 1}{2 x}}$ thì $\cot α$ bằng:

A. $\frac{\sqrt{x^{2} - 1}}{x}$

B. $\frac{\sqrt{x - 1}}{x + 1}$

C. $\frac{\sqrt{x^{2} - 1}}{x^{2} - 1}$

D. $\frac{1}{\sqrt{x^{2} + 1}}$

Xem đáp án

Ta có: $0 < α < 90^{0} \Leftrightarrow 0 < \frac{α}{2} < 45^{0} \Rightarrow 0 < \sin \frac{α}{2} < \frac{\sqrt{2}}{2}$

$\Leftrightarrow 0 < \sqrt{\frac{x - 1}{2 x}} < \frac{\sqrt{2}}{2} \Leftrightarrow x > 0$

$\sin^{2} \frac{α}{2} + \cos^{2} \frac{α}{2} = 1 \Rightarrow \cos \frac{α}{2} = \sqrt{1 - \sin^{2} \frac{α}{2}}$

vì $0 < \frac{α}{2} < 45^{0}$

$\Leftrightarrow \cos \frac{α}{2} = \sqrt{\frac{x + 1}{2 x}} \Rightarrow \tan \frac{α}{2} = \sqrt{\frac{x - 1}{x + 1}}$

$\tan α = \frac{2 \tan \frac{α}{2}}{1 - \tan^{2} \frac{α}{2}} = \frac{2 \sqrt{\frac{x - 1}{x + 1}}}{1 - \frac{x - 1}{x + 1}} = \sqrt{x^{2} - 1}$

$\Rightarrow \cot α = \frac{1}{\tan α} = \frac{1}{\sqrt{x^{2} - 1}} = \frac{\sqrt{x^{2} - 1}}{x^{2} - 1}$

Đáp án cần chọn là: C

Câu 10:

Xét tính chất của tam giác ABC biết rằng:

cosA + cosB – cosC + 1 = sinA + sinB + sinC

A. Tam giác ABC vuông cân tại A.

B. Tam giác ABC vuông cân tại C.

C. Tam giác ABC vuông tại C.

D. Tam giác ABC đều.

Xem đáp án

Ta có:

+) $\cos A + \cos B + \cos C + 1 = 2 \cos \frac{A + B}{2} \cos \frac{A - B}{2} + 2 \sin^{2} \frac{C}{2}$

$= 2 \cos (\frac{π}{2} - \frac{C}{2}) \cos \frac{A - B}{2} + 2 \sin^{2} \frac{C}{2}$

$= 2 \sin \frac{C}{2} \cos \frac{A - B}{2} + 2 \sin^{2} \frac{C}{2}$

= $2 \sin \frac{C}{2} (\cos \frac{A - B}{2} + 2 \sin \frac{C}{2})$

$= 2 \sin \frac{C}{2} (\cos \frac{A - B}{2} + \cos \frac{A + B}{2})$

$= 2 \sin \frac{C}{2} .2 \cos \frac{A}{2} \cos \frac{B}{2}$

$= 4 \cos \frac{A}{2} \cos \frac{B}{2} \sin \frac{C}{2}$

+) $\sin A + \sin B + \sin C = 2 \sin \frac{A + B}{2} \cos \frac{A - B}{2} + 2 \sin \frac{C}{2} \cos \frac{C}{2}$

$= 2 \sin (\frac{π}{2} - \frac{C}{2}) \cos \frac{A - B}{2} + 2 \sin \frac{C}{2} \cos \frac{C}{2}$

$= 2 \cos \frac{C}{2} \cos \frac{A - B}{2} + 2 \sin \frac{C}{2} \cos \frac{C}{2}$

= $2 \cos \frac{C}{2} (\cos \frac{A - B}{2} + \sin (\frac{π}{2} - \frac{A + B}{2}))$

$= 2 \cos \frac{C}{2} (\cos \frac{A - B}{2} + \cos \frac{A + B}{2})$

$= 2 \cos \frac{C}{2} .2 \cos \frac{A}{2} \cos \frac{B}{2}$

$= 4 \cos \frac{A}{2} \cos \frac{B}{2} \cos \frac{C}{2}$

$\Rightarrow \frac{\cos A + \cos B + \cos C + 1}{\sin A + \sin B + \sin C} = \frac{4 \cos \frac{A}{2} \cos \frac{B}{2} \sin \frac{C}{2}}{4 \cos \frac{A}{2} \cos \frac{B}{2} \cos \frac{C}{2}} = \tan \frac{C}{2}$

$\Rightarrow \tan \frac{C}{2} = 1 \Leftrightarrow \frac{C}{2} = 45^{0} \Leftrightarrow C = 90^{0}$

$\Rightarrow Δ A B C$ vuông tại C

Đáp án cần chọn là: C

Câu 11:

Hãy xác định hệ thức sai:

A. $\sin x \cos^{3} x - \cos x \sin^{3} x = \frac{\sin 4 x}{4}$

B. $\sin^{4} x + \cos^{4} x = \frac{3 + \cos 4 x}{4}$

C. $\frac{1 + s inx}{\cos x} = \cot (\frac{π}{4} + \frac{x}{2})$

D. $\cot^{2} x + \tan^{2} x = \frac{2 \cos 4 x + 6}{1 - \cos 4 x}$

Xem đáp án

+) $\sin x \cos^{3} x - \cos x \sin^{3} x = s inx \frac{3 \cos x + \cos 3 x}{4} - \cos x . \frac{3 \sin x - \sin 3 x}{4}$

$= \frac{3}{4} \sin x \cos x + \frac{1}{4} \sin x \cos 3 x - \frac{3}{4} \sin x \cos x + \frac{1}{4} \sin 3 x \cos x$

$= \frac{1}{4} (\sin x \cos 3 x + \sin 3 x \cos x)$

$= \frac{1}{4} \sin (x + 3 x) = \frac{\sin 4 x}{4}$

+) $\sin^{4} x + \cos^{4} x = {(\sin^{2} x + \cos^{2} x)}^{2} - 2 \sin^{2} x \cos^{2} x = 1 - \frac{1}{2} \sin^{2} 2 x$

$= 1 - \frac{1}{2} - \frac{1 - \cos 4 x}{2} = \frac{3 + \cos 4 x}{4}$

+) $\cot^{2} x + \tan^{2} x = \frac{\cos^{2} x}{\sin^{2} x} + \frac{\sin^{2} x}{\cos^{2} x} = \frac{\cos^{4} x + \sin^{4} x}{\sin^{2} x \cos^{2} x}$

$= \frac{\frac{3 + \cos 4 x}{4}}{\frac{1}{4} \sin^{2} 2 x}$

$= \frac{3 + \cos 4 x}{\frac{1}{2} (1 - \cos 4 x)} = \frac{2 \cos 4 x + 6}{1 - \cos 4 x}$

Đáp án cần chọn là: C

Câu 12:

Nếu $\sin a - \cos a = \frac{1}{5} (135^{0} < a < 180^{0})$ thì giá trị đúng của tan2a là:

A. $- \frac{20}{7}$

B. $\frac{20}{7}$

C. $\frac{24}{7}$

D. $- \frac{24}{7}$

Xem đáp án

$\sin a - \cos a = \frac{1}{5} \Rightarrow {(\sin a - \cos a)}^{2} = \frac{1}{25}$

$\Leftrightarrow \sin^{2} a - 2 \sin a \cos a + \cos^{2} a = \frac{1}{25}$

$\Leftrightarrow 1 - \sin 2 a = \frac{1}{25} \Leftrightarrow \sin 2 a = \frac{24}{25}$

Ta có:

$\sin^{2} 2 a + \cos^{2} 2 a = 1 \Rightarrow {(\frac{24}{25})}^{2} + \cos^{2} 2 a = 1$

$\Leftrightarrow \cos^{2} 2 a = \frac{49}{625} \Leftrightarrow \cos 2 a = \pm \frac{7}{25}$

Mà $135^{0} < a < 180^{0} \Leftrightarrow 270^{0} < 2 a < 360^{0}$

$\Rightarrow \cos 2 a > 0 \Rightarrow \cos 2 a = \frac{7}{25}$

$\tan 2 a = \frac{\sin 2 a}{\cos 2 a} = \frac{\frac{24}{25}}{\frac{7}{25}} = \frac{24}{7}$

Đáp án cần chọn là: C

Câu 13:

Biểu thức $\frac{2 \cos^{2} x - 1}{4 \tan (\frac{π}{4} - x) \sin^{2} (\frac{π}{4} + x)}$ có kết quả rút gọn bằng:

A. $\frac{1}{2}$

B. $\frac{1}{4}$

C. $\frac{1}{8}$

D. $\frac{1}{12}$

Xem đáp án

$\frac{2 \cos^{2} x - 1}{4 \tan (\frac{π}{4} - x) \sin^{2} (\frac{π}{4} + x)} = \frac{\cos 2 x}{4. \frac{\sin (\frac{π}{4} - x)}{\cos (\frac{π}{4} - x)} . \frac{1 - \cos (\frac{π}{2} + 2 x)}{2}}$

$= \frac{\cos 2 x}{2. \frac{\sqrt{2} (\cos x - s inx)}{\sqrt{2} (\cos x + s inx)} . (1 + s in2x)}$

$= \frac{\cos 2 x}{2. \frac{(\cos x - s inx)}{(\cos x + s inx)} . {(\sin x + \cos x)}^{2}}$

$= \frac{\cos 2 x}{2 (\cos x - s inx) (s inx + \cos x)}$

$= \frac{\cos 2 x}{2 (\cos^{2} x - \sin^{2} x)} = \frac{\cos 2 x}{2 \cos 2 x} = \frac{1}{2}$

Đáp án cần chọn là: A

Câu 14:

Rút gọn biểu thức $B = \sin^{3} \frac{a}{3} + 3 \sin^{3} \frac{a}{3^{2}} + 3^{2} \sin^{3} \frac{a}{3^{3}} + ... + 3^{n - 1} \sin^{3} \frac{a}{3^{n}}$ bằng:

A. $B = \frac{3^{n} \sin \frac{a}{3^{n}} - 3 \sin a}{4}$

B. $B = \frac{3^{n} \sin \frac{a}{3^{n}} - \sin a}{4}$

C. $B = \frac{3^{n + 1} \sin \frac{a}{3^{n}} - \sin a}{2}$

D. $B = \frac{3^{n - 1} \sin \frac{a}{3^{n}}}{2}$

Xem đáp án

$B = \sin^{3} \frac{a}{3} + 3 \sin^{3} \frac{a}{3^{2}} + 3^{2} \sin^{3} \frac{a}{3^{3}} + ... + 3^{n - 1} \sin^{3} \frac{a}{3^{n}}$

$= \frac{3 \sin \frac{a}{3} - \sin a}{4} + 3. \frac{3 \sin \frac{a}{3^{2}} - \sin \frac{a}{3}}{4} + 3^{2} . \frac{3 \sin \frac{a}{3^{3}} - \sin \frac{a}{3^{2}}}{4} + ... + 3^{n - 1} . \frac{3 \sin \frac{a}{3^{n}} - \sin \frac{a}{3^{n - 1}}}{4}$

= $\frac{1}{4} . (- \sin a + 3 \sin \frac{a}{3} - 3 \sin \frac{a}{3} + 3^{2} \sin \frac{a}{3^{2}} - 3^{2} \sin \frac{a}{3^{2}} + 3^{3} \sin \frac{a}{3^{3}} - ... - 3^{n - 1} \sin \frac{a}{3^{n - 1}} + 3^{n} \sin \frac{a}{3^{n}})$

= $\frac{1}{4} (3^{n} \sin \frac{a}{3^{n}} - \sin a)$

= $\frac{3^{n} \sin \frac{a}{3^{n}} - \sin a}{4}$

Đáp án cần chọn là: B

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Ôn tập chương VI toán 10 có đáp án

Trắc nghiệm Ôn tập chương VI có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương