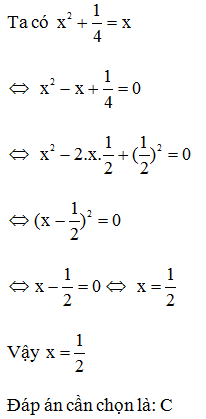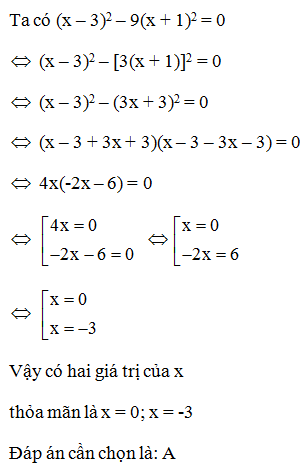11 câu hỏi trắc nghiệm thuộc Trắc nghiệm Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức có đáp án (Thông hiểu) - hamchoi.vn

Trắc nghiệm Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức có đáp án

Trắc nghiệm Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức có đáp án (Thông hiểu)

1786 lượt thi
11 câu hỏi
30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Cho (4x² + 2x – 18)² – (4x² + 2x)² = m.(4x² + 2x – 9). Khi đó giá trị của m là:

A. m = -18

B. m = 36

C. m = -36

D. m = 18

Ta có (4x² + 2x – 18)² – (4x² + 2x)²

= (4x² + 2x – 18 + 4x² + 2x)(4x² + 2x – 18 – 4x² – 2x)

= (8x² + 4x – 18)(-18) = 2(4x² + 2x – 9)(-18)

= (-36)(4x² + 2x – 9) => m = -36

Đáp án cần chọn là: C

Câu 2:

Giá trị của x thỏa mãn 5x² – 10x + 5 = 0

A. 1

B. -1

C. 2

D. 5

Ta có 5x² – 10x + 5 = 0

5(x² – 2x + 1) = 0

5(x – 1)² = 0

x – 1 = 0

x = 1

Vậy x = 1

Đáp án cần chọn là: A

Câu 3:

Giá trị của x thỏa mãn $x^{2} + \frac{1}{4} = x$ là

A. 2

B. $- \frac{1}{2}$

C. $\frac{1}{2}$

D. -2

Câu 4:

Có bao nhiêu giá trị của x thỏa mãn (2x – 5)² – 4(x – 2)² = 0?

A. 2

B. 1

C. 0

D. 4

Ta có (2x – 5)² – 4(x – 2)² = 0

(2x – 5)² – [2(x – 2)]² = 0

(2x – 5)² – (2x – 4)² = 0

(2x – 5 + 2x – 4)(2x – 5 – 2x + 4) = 0

(4x – 9).(-1) = 0

-4x + 9 = 0

4x = 9

$x = \frac{9}{4}$

Đáp án cần chọn là: B

Câu 5:

Có bao nhiêu giá trị của x thỏa mãn (x – 3)² – 9(x + 1)² = 0?

A. 2

B. 1

C. 0

D. 4

Câu 6:

Cho x – 4 = -2y. Khi đó giá trị của biểu thức M = (x + 2y – 3)² – 4(x + 2y – 3) + 4 bằng

A. M = 0

B. M = -1

C. M = 1

D. Đáp án khác

Ta có M = (x + 2y – 3)² – 4(x + 2y – 3) + 4

= (x + 2y – 3)² – 2(x + 2y – 3).2 + 2²

= (x + 2y – 3 – 2)² = (x + 2y – 5)²

Ta có x – 4 = -2y x + 2y = 4

Thay x + 2y = 4 vào M ta được

M = (4 – 5)² = (-1)² = 1

Vậy M = 1

Đáp án cần chọn là: C

Câu 7:

Đa thức 4b²c² – (c² + b² – a²)² được phân tích thành

A.(b + c + a)(b + c – a)(a + b – c)(a – b + c)

B.(b + c + a)(b – c – a)(a + b – c)(a – b + c)

C.(b + c + a)(b + c – a)(a + b – c)²

D.(b + c + a)(b + c – a)(a + b – c)(a – b – c)

Ta có 4b²c² – (c² + b² – a²)²

= (2bc)² – (c² + b² – a²)²

= (2bc + c² + b² – a²)(2bc – c² – b² + a²)

= [(b + c)² – a²][a² – (b² – 2bc + c²)]

= [(b + c)² – a²][a² – (b – c)²]

= (b + c + a)(b + c – a)(a + b – c)(a – b + c)

Đáp án cần chọn là: A

Câu 8:

Đa thức x⁶ – y⁶ được phân tích thành

A.(x + y)²(x² – xy + y²)(x² + xy + y²)

B.(x + y)(x² – 2xy + y²)(x – y)(x² + 2xy + y²)

C.(x + y)(x² – xy + y²)(x – y)(x² + xy + y²)

D.(x + y)(x² + 2xy + y²)(y – x)(x² + xy + y²)

Ta có

x⁶ – y⁶ = (x³)² – (y³)² = (x³ + y³)(x³ – y³)

= (x + y)(x² – xy + y²)(x – y)(x² + xy + y²)

Đáp án cần chọn là: C

Câu 9:

Tính giá trị biểu thức P = x³ – 3x² + 3x với x = 101

A. 100³+ 1

B. 100³ – 1

C. 100³

D. 101³

Ta có

P = x³ – 3x² + 3x – 1 + 1 = (x – 1)³ + 1

Thay x = 101 vào P ta được

P = (101 – 1)³ + 1 = 100³ + 1

Đáp án cần chọn là: A

Câu 10:

Cho (4x² + 4x – 3)² – (4x² + 4x + 3)² = m.x(x + 1) với m R. Chọn câu đúng về giá trị của m.

A. m > 47

B. m < 0

C. m = 9

D. m là số nguyên tố

Ta có (4x² + 4x – 3)² – (4x² + 4x + 3)²

= (4x² + 4x – 3 + 4x² + 4x + 3)(4x² + 4x – 3 – 4x² – 4x – 3)

= (8x² + 8x).(-6) = 8.x(x + 1).(-6)

= -48x(x + 1) nên m = -48 < 0

Đáp án cần chọn là: B

Câu 11:

Phân tích đa thức $\frac{1}{64} x^{6} + 125 y^{3}$ thành nhân tử, ta được

A. $(\frac{x^{2}}{4} + 5 y) (\frac{x^{2}}{4} - \frac{5}{4} x^{2} y + 5 y^{2})$

B. $(\frac{x^{2}}{4} - 5 y) (\frac{x^{4}}{16} + \frac{5}{4} x^{2} y + 25 y^{2})$

C. $(\frac{x^{2}}{4} + 5 y) (\frac{x^{4}}{16} - \frac{5}{4} x^{2} y + 25 y^{2})$

D. $(\frac{x^{2}}{4} + 5 y) (\frac{x^{4}}{16} - \frac{5}{2} x^{2} y + 25 y^{2})$

Bắt đầu thi ngay

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương