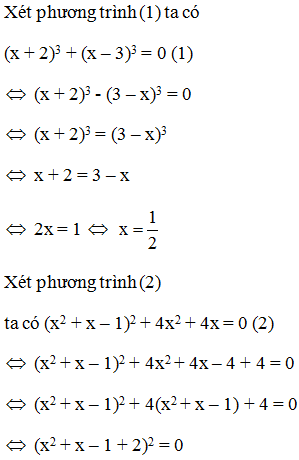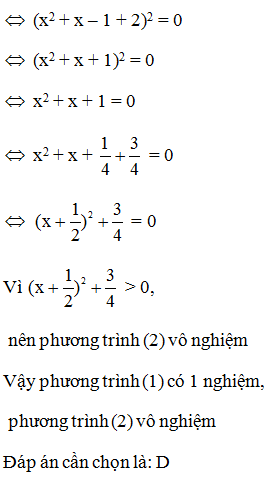Trắc nghiệm Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức có đáp án
Trắc nghiệm Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức có đáp án (Vận dụng)
-
1787 lượt thi
-
10 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho 9a2 – (a – 3b)2 = (m.a + n.b)(4a – 3b) với m, n R. Khi đó, giá trị của m và n là
Xem đáp án
Ta có 9a2 – (a – 3b)2 = (3a)2 – (a – 3b)2 = (3a + a – 3b)(3a – a + 3b)
= (4a – 3b)(2a + 3b)
Suy ra m = 2; n = 3
Đáp án cần chọn là: D
Câu 2:
Cho x + n = 2(y – m), khi đó giá trị của biểu thức A = x2 – 4xy + 4y2 – 4m2 – 4mn – n2 bằng
Xem đáp án
Ta có A = x2 – 4xy + 4y2 – 4m2 – 4mn – n2
= x2 – 2x.2y + (2y)2 – (4m2 + 4mn + n2)
= (x – 2y)2 – (2m + n)2
= (x – 2y + 2m + n)(x – 2y – 2m – n)
Ta có x + n = 2(y – m)
x + n = 2y – 2m
x – 2y + n + 2m = 0
Thay x – 2y + n + 2m = 0 vào A ta được
A = 0.(x – 2y – 2m – n) = 0
Vậy A = 0
Đáp án cần chọn là: B
Câu 3:
Hiệu bình phương các số lẻ liên tiếp thì luôn chia hết cho
Xem đáp án
Gọi hai số lẻ liên tiếp là 2k – 1; 2k + 1 (k N*)
Theo bài ra ta có
(2k + 1)2 – (2k – 1)2 = 4k2 + 4k + 1 – 4k2 + 4k – 1 = 8k = 8
Đáp án cần chọn là: A
Câu 4:
Có bao nhiêu cặp số nguyên (x; y) thỏa mãn x2 + 102 = y2
Xem đáp án
Ta có x2 + 102 = y2 y2 – x2 = 102
Nhận thấy hiệu hai bình phương là một số chẵn nên x, y cùng là số chẵn hoặc cùng là số lẻ
Suy ra y – x; y + x luôn là số chẵn
Lại có y2 – x2 = 102 (y – x)(y + x) = 102
Mà (y – x) và (y + x) cùng là số chẵn.
Suy ra (y – x)(y + x) chia hết cho 4 mà 102 không chia hết cho 4 nên không tồn tại cặp số x; y thỏa mãn đề bài
Đáp án cần chọn là: A
Câu 5:
Cho x + y = a + b; x2 + y2 = a2 + b2. Với n N*, chọn câu đúng
Xem đáp án
Ta có: x2 + y2 = a2 + b2 x2 – a2 = b2 – y2
(x – a)(x + a) = (b – y)(b + y)
Mà x + y = a + b x – a = b – y nên ta có
(x – a)(x + a) = (x – a)(b + y)
(x – a)(x + a) – (x – a)(b + y) = 0
(x – a)(x + a – b – y) = 0
<=>
+) Với x = a
Ta có: x + y = a + b a + y = a + b y = b
Do đó: xn + yn = an + bn
+) Với x - y = b - a x = b - a + y thay vào x + y = a + b ta được
b - a + y + y = a + b 2y = 2a y = a x = b - a + a = b
Do đó: xn + yn = bn + an = an + bn
Đáp án cần chọn là: C
Câu 6:
Gọi x1; x2; x3 là các giá trị thỏa mãn 4(3x – 5)2 – 9(9x2 – 25)2 = 0. Khi đó x1 + x2 + x3 bằng
Xem đáp án
Ta có 4(3x – 5)2 – 9(9x2 – 25)2 = 0
4(3x – 5)2 – 9[(3x)2 – 52]2 = 0
4(3x – 5)2 – 9[(3x – 5)(3x + 5)]2 = 0
4(3x – 5)2 – 9(3x – 5)2(3x + 5)2 = 0
(3x – 5)2[4 – 9(3x + 5)2] = 0
(3x – 5)2[4 – (3(3x + 5))2] = 0
(3x – 5)2(22 – (9x + 15)2) = 0
(3x – 5)2(2 + 9x + 15)(2 – 9x – 15) = 0
(3x – 5)2(9x + 17)(-9x – 13) = 0
<=>
Suy ra
Đáp án cần chọn là: C
Câu 8:
Cho (x2 + y2 – 17)2 – 4(xy – 4)2 = (x + y + 5)(x – y + 3)(x + y + m)(x – y + n). Khi đó giá trị của m.n là
Xem đáp án
Ta có
(x2 + y2 – 17)2 – 4(xy – 4)2 = (x2 + y2 – 17)2 – [2(xy – 4)]2
= (x2 + y2 – 17 + 2xy – 8)(x2 + y2 – 17 – 2xy + 8)
= (x2 + y2 + 2xy – 25)(x2 + y2 – 2xy – 9)
= [(x + y)2 – 52][(x – y)2 – 32]
= (x + y + 5)(x + y – 5)(x – y + 3)(x – y – 3)
Suy ra m = -5; n = -3 => m.n = (-5).(-3) = 15
Đáp án cần chọn là: D
Câu 9:
Cho (x + y)3 – (x – y)3 = A.y(Bx2 + Cy2), biết A, B, C là các số nguyên. Khi đó A + B + C bằng
Xem đáp án
Ta có (x + y)3 – (x – y)3
= [x + y – (x – y)][(x + y)2 + (x + y)(x – y) + (x – y)2]
= (x + y – x + y)(x2 + 2xy + y2 + x2 – y2 + x2 – 2xy + y2)
= 2y(3x2 + y2) => A = 2; B = 3; C = 1
Suy ra A + B + C = 2 + 3 + 1 = 6
Đáp án cần chọn là: C
Câu 10:
Cho x6 – 1 = (x + A)(x + B)(x4 + x2 + C), biết A, B, C là các số nguyên. Khi đó A + B + C bằng
Xem đáp án
Ta có x6 – 1 = (x2)3 – 1 = (x2 – 1)(x4 + x2 + 1)
= (x – 1)(x + 1)(x4 + x2 + 1)
=> A = -1; B = C = 1
Suy ra A + B + C = -1 + 1 + 1 = 1
Đáp án cần chọn là: B