Giải SGK Toán 8 Cánh diều Bài 4. Vận dụng hằng đẳng thức vào phân tích đa thức thành nhân tử có đáp án
Giải SGK Toán 8 Cánh diều Bài 4. Vận dụng hằng đẳng thức vào phân tích đa thức thành nhân tử có đáp án
-
147 lượt thi
-
28 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
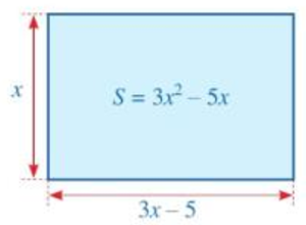
Làm thế nào để biến đổi được đa thức 3x2 – 5x dưới dạng tích của hai đa thức?
 Xem đáp án
Xem đáp án
Để biến đổi được đa thức 3x2 – 5x dưới dạng tích của hai đa thức, ta áp dụng tính chất phân phối của phép nhân đối với phép cộng.
Ta biến đổi như sau: 3x2 – 5x = x(3x – 5).
Câu 2:
Viết đa thức 6x2 – 10x thành tích của hai đa thức bậc nhất.
 Xem đáp án
Xem đáp án
Đa thức 6x2 – 10x thành tích của hai đa thức bậc nhất như sau:
6x2 – 10x = 3x(x – 5).
Câu 3:
Viết đa thức 6x2 – 10x thành tích của hai đa thức bậc nhất.
 Xem đáp án
Xem đáp án
Đa thức 6x2 – 10x thành tích của hai đa thức bậc nhất như sau:
6x2 – 10x = 3x(x – 5)
Câu 4:
Viết mỗi đa thức sau dưới dạng tích của hai đa thức:
a) x2 – y2;
 Xem đáp án
Xem đáp án
a) x2 – y2 = (x + y)(x – y);
Câu 7:
Phân tích mỗi đa thức sau thành nhân tử:
a) (x + 2y)2 – (2x – y)2;
 Xem đáp án
Xem đáp án
a) (x + 2y)2 – (2x – y)2 = [(x + 2y) + (2x – y)] [(x + 2y) – (2x – y)]
= (x + 2y + 2x – y)(x + 2y – 2x + y) = (3x + y)(3y – x);
Câu 10:
Cho đa thức x2 – 2xy + y2 + x – y.
a) Nhóm ba số hạng đầu và sử dụng hằng đẳng thức để viết nhóm đó thành tích.
 Xem đáp án
Xem đáp án
Cho đa thức x2 – 2xy + y2 + x – y.
a) Nhóm ba số hạng đầu và sử dụng hằng đẳng thức để viết nhóm đó thành tích, ta được:
x2 – 2xy + y2 + x – y
= (x2 – 2xy + y2) + (x – y) (nhóm ba số hạng đầu, hai số hạng cuối thành nhóm)
= (x – y)2 + (x – y) (dùng hằng đẳng thức để viết nhóm thứ nhất thành tích)
= (x – y)(x – y + 1) (đặt nhân tử chung ở hai nhóm ra ngoài để viết thành tích)
Câu 11:
b) Phân tích đa thức trên thành nhân tử.
 Xem đáp án
Xem đáp án
b) Đa thức trên được phân tích thành nhân tử như sau:
x2 – 2xy + y2 + x – y = (x – y)(x – y + 1).
Câu 12:
Phân tích mỗi đa thức sau thành nhân tử:
a) 3x2 – 6xy + 3y2 – 5x + 5y;
 Xem đáp án
Xem đáp án
a) 3x2 – 6xy + 3y2 – 5x + 5y
= 3(x2 – 2xy + y2) – (5x – 5y)
= 3(x – y)2 – 5(x – y) = (x – y)[3(x – y) – 5]
= (x – y)(3x – 3y) – 5).
Câu 13:
b) 2x2y + 4xy2 + 2y3 – 8y.
 Xem đáp án
Xem đáp án
b) 2x2y + 4xy2 + 2y3 – 8y
= 2y(x2 + 2xy + y2 – 4)
= 2y[(x + y)2 – 22]
= 2y(x + y + 2)(x + y – 2).
Câu 14:
Phân tích mỗi đa thức sau thành nhân tử:
a) 4x2 – 12xy + 9y2;
 Xem đáp án
Xem đáp án
a) 4x2 – 12xy + 9y2 = (2x)2 – 2 . 2x . 3y + (3y)2 = (2x – 3y)2;
Câu 15:
b) x3 + 6x2 + 12x + 8;
 Xem đáp án
Xem đáp án
b) x3 + 6x2 + 12x + 8 = x3 + 3 . x2 . 2 + 3 . x . 22 + 23 = (x + 3)3;
Câu 16:
c) 8y3 – 12y2 + 6y – 1;
 Xem đáp án
Xem đáp án
c) 8y3 – 12y2 + 6y – 1 = (2y)3 – 3 . (2y)2 . 1 + 3 . 2y . 1 – 13 = (2y – 1)3;
Câu 17:
d) (2x + y)2 – 4y2;
 Xem đáp án
Xem đáp án
d) (2x + y)2 – 4y2 = (2x + y + 4y)(2x + y – 4y) = (2x + 5y)(2x – 3y);
Câu 18:
e) 27y3 + 8;
 Xem đáp án
Xem đáp án
e) 27y3 + 8 = (3y)3 + 23 = (3y + 2)[(3y)2 – 3y . 2 + 22]
= (3y + 2)(9y2 – 6y + 4);
Câu 19:
g) 64 – 125x3.
 Xem đáp án
Xem đáp án
g) 64 – 125x3 = 43 – (5x)3 = (4 + 5x)[42 + 4 . 5x + (5x)2]
= (4 + 5x)(16 + 20x + 25x2).
Câu 20:
Phân tích mỗi đa thức sau thành nhân tử:
a) x2 – 25 + 4xy + 4y2;
 Xem đáp án
Xem đáp án
a) x2 – 25 + 4xy + 4y2 = (x2 + 4xy + 4y2) – 25
= (x + 2y)2 – 52 = (x + 2y + 5)(x + 2y – 5);
Câu 21:
b) x3 – y3 + x2y – xy2;
 Xem đáp án
Xem đáp án
b) x3 – y3 + x2y – xy2 = (x3 + x2y) – (y3 + xy2)
= (x3 + x2y) – (y3 + xy2) = x2(x + y) – y2(x + y)
= (x + y)(x2 – y2) = (x + y)(x + y)(x – y) = (x + y)2(x – y);
Câu 22:
c) x4 – y4 + x3y – xy3.
 Xem đáp án
Xem đáp án
c) x4 – y4 + x3y – xy3 = (x4 + x3y) – (y4 + xy3)
= x3(x + y) – y3(x + y) = (x + y)(x3 – y3)
= (x + y)(x – y)(x2 + xy + y2).
Câu 23:
Tính giá trị của mỗi biểu thức sau:
a) A = x4 – 2x2y – x2 + y2 + y biết x2 – y = 6;
 Xem đáp án
Xem đáp án
a) Ta có A = x4 – 2x2y – x2 + y2 + y
= (x4 – 2x2y + y2) – (x2 – y)
= [(x2)2 – 2x2y + y2] – (x2 – y)
= (x2 – y)2 – (x2 – y).
Giá trị của mỗi biểu thức A với x2 – y = 6 là:
A = (x2 – y)2 – (x2 – y) = 62 – 6 = 36 – 6 = 30.
Câu 24:
b) B = x2y2 + 2xyz + z2 biết xy + z = 0.
 Xem đáp án
Xem đáp án
b) B = x2y2 + 2xyz + z2 = (xy)2 + 2xyz + z2 = (xy + z)2.
Giá trị của mỗi biểu thức tại xy + z = 0 là: B = (xy + z)2 = 02 = 0.
Câu 25:
Chứng tỏ rằng:
a) M = 322 023 – 322 021 chia hết cho 31;
 Xem đáp án
Xem đáp án
a) Ta có M = 322 023 – 322 021 = 322 . 322 021 – 322 021
= (322 – 1) . 322 021 = (1024 – 1) . 322 021 = 1023 . 322 021
Vì 1023 ⋮ 31 nên (1023 . 322 021) ⋮ 31.
Do đó M = 322 023 – 322 021 chia hết cho 31;
Câu 26:
b) N = 76 + 2 . 73 + 82022 +1 chia hết cho 8.
 Xem đáp án
Xem đáp án
b) Ta có N = 76 + 2 . 73 + 82022 +1 = (73)2 + 2 . 73 +1 + 82022
= (73 + 1)2 + 82022 = 3442 + 82022.
Vì 344 ⋮ 8; 8 ⋮ 8 nên 3442 ⋮ 8; 82022 ⋮ 8.
Do đó (3442 + 82022) ⋮ 8
Vậy N = 76 + 2 . 73 + 82022 +1 chia hết cho 8.
Câu 27:
Bác Hoa gửi tiết kiệm a đồng kì hạn 12 tháng ở một ngân hàng với lãi suất x%/năm.
a) Viết công thức tính số tiền bác Hoa có được sau 12 tháng dưới dạng tích, biết bác Hoa không rút tiền ra khỏi ngân hàng trong 12 tháng đó.
 Xem đáp án
Xem đáp án
a) Số tiền lãi bác Hoa nhận được sau 12 tháng là: a . r% (đồng)
Do đó, công thức tính số tiền bác Hoa có được sau 12 tháng là:
a + a . r% = a . (1 + r%) (đồng).
Câu 28:
b) Sau kì hạn 12 tháng, tiền lãi của kì hạn đó được cộng vào tiền vốn, rồi bác Hoa tiếp tục đem gửi cho kì hạn 12 tháng tiếp theo. Viết công thức tính tổng số tiền mà bác Hoa nhận được sau khi gửi 24 tháng trên dưới dạng tích, biết trong 24 tháng đó, lãi suất ngân hàng không thay đổi và bác Hoa không rút tiền ra khỏi ngân hàng.
 Xem đáp án
Xem đáp án
b) Sau kì hạn 12 tháng, bác Hoa tiếp tục đem gửi cho kì hạn 12 tháng tiếp theo, tức là bác Hoa gửi tiếp 12 tháng với số tiền gốc là a . (1 + r%) (đồng).
Số tiền lãi bác Hoa nhận được sau khi gửi 24 tháng là:
a . (1 + r%) . r% (đồng).
Do đó, công thức tính tổng số tiền mà bác Hoa nhận được sau khi gửi 24 tháng là:
a . (1 + r%) + a . (1 + r%) . r% = a(1 + r%)(1 + r%) = a(1 + r%)2 (đồng).
