Trắc nghiệm chuyên đề Toán 8 Chủ đề 6: Ôn tập và kiểm tra (Có đáp án)
Trắc nghiệm chuyên đề Toán 8 Chủ đề 6: Ôn tập và kiểm tra (Có đáp án)
-
1129 lượt thi
-
55 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Trong các khẳng định sau đây, khẳng định nào đúng?
4 + ( - 3 ) ≤ 5 ( 1 )
6 + ( - 2 ) ≤ 7 + ( - 2 ) ( 2 )
24 + ( - 5 ) > 25 + ( - 6 ) ( 3 )
 Xem đáp án
Xem đáp án
+ Ta có:
⇒ 4 + ( - 3 ) < 4 + 1 hay 4 + ( - 3 ) < 5.
→ Khẳng định ( 1 ) đúng.
+ Ta có:
⇒ 6 + ( - 2 ) < 7 + ( - 2 )
→ Khẳng định ( 2 ) đúng.
+ Ta có: 24 < 25 ⇒ 24 + ( - 5 ) < 25 + ( - 5 )
→ Khẳng định ( 3 ) sai.
Chọn đáp án C.
Câu 2:
Cho a - 3 > b - 3. So sánh hai số a và b
 Xem đáp án
Xem đáp án
Ta có a - 3 > b - 3 ⇒ ( a - 3 ) + 3 > ( b - 3 ) + 3 ⇔ a > b
Chọn đáp án C.
Câu 3:
Cho a > b. So sánh 5 - a với 5 - b
 Xem đáp án
Xem đáp án
Ta có: a > b ⇒ - a < - b ⇔ 5 + ( - a ) < 5 + ( - b ) hay 5 - a < 5 - b.
Chọn đáp án D.
Câu 4:
Một Ampe kế có giới hạn đo là 25 ampe. Gọi x( A ) là số đo cường độ dòng điện có thể đo bằng Ampe kế. Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Một Ampe kế đo cường độ dòng điện thì cường độ dòng điện tối đa mà Ampe đo được là giới hạn đo của ampe kế đó.
Khi đó: x ≤ 25
Chọn đáp án A.
Câu 5:
Cho a > b, c > d. Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Theo giả thiết ta có: a > b, c > d ⇒ a + c > b + d.
Chọn đáp án B.
Câu 6:
Trong các khẳng định sau đây, khẳng định nào sai?
( 1 ) ( - 4 ).5 ≤ ( - 5 ).4
( 2 ) ( - 7 ).12 ≥ ( - 7 ).11
( 3 ) - 4x2 > 0
 Xem đáp án
Xem đáp án
+ Ta có: ( - 4 ).5 = 4.( - 5 ) → Khẳng định ( 1 ) sai.
+ Ta có: 12 > 11 ⇒ 12.( - 7 ) < 11.( - 7 ) → Khẳng định ( 2 ) sai.
+ Ta có: x2 ≥ 0 ⇒ - 4x2 ≤ 0 → Khẳng định ( 3 ) sai
Chọn đáp án A.
Câu 7:
Cho a + 1 ≤ b + 2. So sánh hai số 2a + 2 và 2b + 4 nào dưới đây đúng ?
 Xem đáp án
Xem đáp án
Với ba số a, b và c mà c > 0, ta có: Nếu a ≤ b thì ac ≤ bc
Khi đó, ta có: a + 1 ≤ b + 2 ⇒ 2( a + 1 ) ≤ 2( b + 2 ) ⇔ 2a + 2 ≤ 2b + 4.
Chọn đáp án C.
Câu 8:
Cho a > b. Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
+ Ta có: a > b ⇒ - 3a < - 3b ⇔ - 3a - 1 < - 3b - 1
→ Đáp án A sai.
+ Ta có: a > b ⇒ a - 1 > b - 1 ⇔ - 3( a - 1 ) < - 3( b - 1 )
→ Đáp án B đúng.
+ Ta có: a > b ⇒ a - 1 > b - 1 ⇔ - 3( a - 1 ) < - 3( b - 1 )
→ Đáp án C sai.
+ Ta có: a > b ⇒ a - 1 > b - 1 ⇔ 3( a - 1 ) > 3( b - 1 )
→ Đáp án D sai.
Chọn đáp án B.
Câu 9:
 Xem đáp án
Xem đáp án
+ Ta có: a ≥ b ⇒ 2a ≥ 2b
Mặt khác, ta có: - 5 ≥ - 6
Khi đó 2a - 5 ≥ 2b - 6 hay 2a - 5 ≥ 2( b - 3 ).
Chọn đáp án C.
Câu 10:
Cho x > 0. Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Ta có: x > 0 ⇒ x + 1 > 1 ⇒ ( x + 1 )2 > 12.
Hay ( x + 1 )2 > 1.
Chọn đáp án B.
Câu 11:
Nghiệm x = 3 là nghiệm của bất phương trình nào sau đây?
 Xem đáp án
Xem đáp án
Ta có:
+ 5 - x < 1 ⇔ 4 < x
+ 3x + 1 < 4 ⇔ 3x < 2 ⇔ x > 2/3
+ 4x - 11 > x ⇔ 3x > 11 ⇔ x > 11/3
+ 2x - 1 > 3 ⇔ 2x > 4 ⇔ x > 2
Vậy x = 3 là nghiệm của bất phương trình 2x - 1 > 3
Chọn đáp án D.
Câu 12:
Tập nghiệm nào sau đây là tập nghiệm của bất phương trình: x ≤ 2 ?
 Xem đáp án
Xem đáp án
Tập nghiệm của bất phương trình: x ≤ 2 là S = { x| x ≤ 2 }.
Chọn đáp án B.
Câu 13:
Hình vẽ sau là tập nghiệm của bất phương trình nào?
 Xem đáp án
Xem đáp án
Ta có:
+ 2x - 4 < 0 ⇔ x < 2
+ 2x - 4 > 0 ⇔ x > 2
+ 2x - 4 ≤ 0 ⇔ x ≤ 2
+ 2x - 4 ≥ 0 ⇔ x ≥ 2
Chọn đáp án B.
Câu 14:
Cho bất phương trình 3x - 6 > 0. Trong các bất phương trình sau, bất phương trình nào tương đương với bất phương trình đã cho?
 Xem đáp án
Xem đáp án
Ta có: 3x - 6 > 0 ⇔ 3x > 6 ⇔ x > 2
Vậy bất phương trình x > 2 tương đương với bất phương trình đã cho.
Chọn đáp án C.
Câu 15:
Bất phương trình ax + b > 0 vô nghiệm khi
 Xem đáp án
Xem đáp án
Nếu a > 0 thì ax + b > 0 ⇔ x > - b/a nên
Nếu a < 0 thì ax + b > 0 ⇔ x < - b/a nên
Nếu a = 0 thì ax + b > 0 có dạng 0x + b > 0
Với b > 0 thì S = R.
Với b ≤ 0 thì S = Ø
Chọn đáp án D.
Câu 16:
Bất phương trình ax + b ≤ 0 vô nghiệm khi?
 Xem đáp án
Xem đáp án
Nếu a > 0 thì ax + b ≤ 0 ⇔ x ≤ - b/a nên
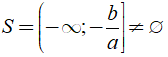
Nếu a < 0 thì ax + b ≤ 0 ⇔ x ≥ - b/a nên
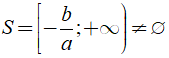
Nếu a = 0 thì ax + b ≤ 0 có dạng 0x + b ≤ 0
Với b ≤ 0 thì S = R.
Với b > 0 thì S = Ø
Chọn đáp án A.
Câu 17:
Tổng các nghiệm nguyên của bất phương trình x( 2 - x ) ≥ x( 7 - x ) - 6( x - 1 ) trên đoạn [ - 10;10 ] bằng?
 Xem đáp án
Xem đáp án
Ta có: x( 2 - x ) ≥ x( 7 - x ) - 6( x - 1 )
⇔ 2x - x2 ≥ 7x - x2 - 6x + 6
Chọn đáp án D.
Câu 18:
Tổng các nghiệm của bất phương trình:
 Xem đáp án
Xem đáp án
Điều kiện: x > 4
Bất phương trình tương đương: x - 2 ≤ 4 ⇔ x ≤ 6 ⇒ 4 < x ≤ 6 ⇒ x ∈ 5;6 → S = 11
Chọn đáp án B.
Câu 19:
Tập nghiệm của bất phương trình: ( x - 1 )2 + ( x - 3 )2 + 15 < x2 + ( x - 4 )2 là?
 Xem đáp án
Xem đáp án
Bất phương trình tương đương: 2x2 - 8x + 10 + 15 < 2x2 - 8x + 16
⇔ 0.x < - 9 : Vô nghiệm.
Chọn đáp án D.
Câu 20:
Tập nghiệm S của bất phương trình: 5x - 1 ≥ + 3 là?
 Xem đáp án
Xem đáp án
Ta có: 5x - 1 ≥ (2x)/5 + 3 ⇔ 25x - 5 ≥ 2x + 15 ⇔ 23x ≥ 20 ⇔ x ≥ 20/23.
Vậy tập nghiệm của bất phương trình là [ 20/23; + ∞ )
Chọn đáp án D.
Câu 21:
Bất phương trình
có bao nhiêu nghiệm nguyên lớn hơn -10 ?
 Xem đáp án
Xem đáp án
Ta có:
⇔ 9x + 15 - 6 ≤ 2x + 4 + 6 ⇔ x ≤ - 5.
Vì x ∈ Z, - 10 < x ≤ - 5 nên có 5 nghiệm nguyên.
Chọn đáp án B.
Câu 22:
Tập nghiệm S của bất phương trình: ( 1 - √ 2 )x < 3 - 2√ 2 là?
 Xem đáp án
Xem đáp án
Ta có: ( 1 - √ 2 )x < 3 - 2√ 2
Vậy tập nghiệm của bất phương trình là S = ( 1 - √ 2 ; + ∞ )
Chọn đáp án B.
Câu 23:
Bất phương trình ( 2x - 1 )( x + 3 ) - 3x + 1 ≤ ( x - 1 )( x + 3 ) + x2 - 5 có tập nghiệm là?
 Xem đáp án
Xem đáp án
Ta có: ( 2x - 1 )( x + 3 ) - 3x + 1 ≤ ( x - 1 )( x + 3 ) + x2 - 5
⇔ 2x2 + 5x - 3 - 3x + 1 ≤ x2 + 2x - 3 + x2 - 5 ⇔ 0x ≤ - 6
⇔ x ∈ Ø → S = Ø
Chọn đáp án D.
Câu 24:
Bất phương trình ( m2 - 3m )x + m < 2 - 2x vô nghiệm khi?
 Xem đáp án
Xem đáp án
Bất phương trình tương đương: ( m2 - 3m + 2 )x < 2 - m
Rõ ràng nếu m2 - 3m + 2 ≠ 0 ⇔
bất phương trình luôn có nghiệm.
Với m = 1, bất phương trình trở thành: 0x < 1: Vô nghiệm
Với m = 2, bất phương trình trở thành 0x < 0: Vô nghiệm
Chọn đáp án C.
Câu 25:
Bất phương trình m2( x - 1 ) ≥ 9x + 3m có nghiệm đúng với mọi x khi?
 Xem đáp án
Xem đáp án
Bất phương trình tương đương: ( m2 - 9 )x ≥ m2 + 3m
Dễ thấy nếu m2 ≠ 9 ⇔ m ≠ ± 3 thì phương trình không thể có nghiệm đúng với mọi x ∈ R
Với m = 3, ta có bất phương trình trở thành: 0x > 18: Vô nghiệm.
Với m = - 3, ta có phương trình trở thành: 0x ≥ 0: Nghiệm đúng với mọi x ∈ R
Chọn đáp án B.
Câu 26:
Tìm tất cả các giá trị của tham số m để bất phương trình m( x - 1 ) < 3 - x có nghiệm?
 Xem đáp án
Xem đáp án
Bất phương trình tương đương là ( m + 1 )x < m + 3
Rõ ràng với m ≠ - 1 thì bất phương trình luôn có nghiệm
Với m = - 1 ta có bất phương trình có dạng: 0x < 2 luôn đúng với mọi x
Vậy bất phương trình có nghiệm với mọi m.
Chọn đáp án C.
Câu 27:
Tìm tất cả các giá trị của tham số m để bất phương trình ( m2 + m - 6 )x ≥ m + 1 có nghiệm?
 Xem đáp án
Xem đáp án
Rõ ràng: m2 + m - 6 ≠ 0 thì bất phương trình luôn có nghiệm
Xét m2 + m - 6 = 0
Từ hai trường hợp, ta được bất phương trình có nghiệm khi m ≠ 2
Chọn đáp án A.
Câu 28:
Biểu thức A = | 4x | + 2x - 1 với x < 0, rút gọn được kết quả là?
 Xem đáp án
Xem đáp án
Ta có: x < 0 ⇒ | 4x | = - 4x
Khi đó ta có: A = | 4x | + 2x - 1 = - 4x + 2x - 1 = - 2x - 1
Chọn đáp án C.
Câu 29:
Tập nghiệm của phương trình: | 3x + 1 | = 5
 Xem đáp án
Xem đáp án
Ta có: | 3x + 1 | = 5 ⇔
Vậy tập nghiệm của phương trình đã cho là S = { - 2;4/3 }
Chọn đáp án C.
Câu 30:
Tập nghiệm của phương trình | 2 - 3x | = | 2 - 5x | là?
 Xem đáp án
Xem đáp án
Ta có: | 2 - 3x | = | 2 - 5x |
Vậy tập nghiệm của phương trình là S = { - 3;7/5 }
Chọn đáp án B.
Câu 31:
 Xem đáp án
Xem đáp án
Phương trình đã cho có nghiệm x = - 1 nên ta có: | 3 + ( - 1 ) | = m ⇔ m = 2.
Vậy m = - 2 là giá trị cần tìm.
Chọn đáp án B.
Câu 32:
Giá trị của m để phương trình | x - m | = 2 có nghiệm là x = 1 ?
 Xem đáp án
Xem đáp án
Phương trình có nghiệm x = 1, khi đó ta có:
Vậy giá trị m cần tìm là m ∈ { - 1;3 }
Chọn đáp án B.
Câu 33:
Khẳng định sau đây đúng hay sai? Vì sao?
a) - 6 > 5 - 10
 Xem đáp án
Xem đáp án
a) Ta có: VP = 5 - 10 = - 5
Mà - 5 > - 6 ⇒ VP > VT.
Vậy khẳng định trên là sai.
Câu 35:
c) 11 + ( - 6 ) ≤ 10 + ( - 6 )
 Xem đáp án
Xem đáp án
c) Ta có:
⇒ VT = 11 + ( - 6 ) > VP = 10 + ( - 6 )
Khẳng định trên là sai.
Câu 36:
So sánh a và b biết:
a) a - 15 > b - 15
 Xem đáp án
Xem đáp án
a) Ta có: a - 15 > b - 15 ⇔ a - 15 + 15 > b - 15 + 15 ⇔ a > b
Vậy a > b
Câu 37:
b) a + 2 ≤ b + 2
 Xem đáp án
Xem đáp án
b) Ta có: a + 2 ≤ b + 2 ⇒ a + 2 + ( - 2 ) ≤ b + 2 + ( - 2 ) ⇔ a ≤ b
Vậy a ≤ b
Câu 38:
Khẳng định sau đúng hay sai?
a) ( - 3 ).4 > ( - 3 ).3
 Xem đáp án
Xem đáp án
a) Ta có: 4 > 3 ⇒ ( - 3 ).4 < ( - 3 ).3
Khẳng định trên là sai.
Câu 39:
b) ( - 4 )( - 5 ) ≤ ( - 6 )( - 5 )
 Xem đáp án
Xem đáp án
b) Ta có: - 4 ≥ - 6 ⇒ ( - 4 )( - 5 ) ≤ ( - 6 )( - 5 )
Khẳng định trên là đúng
Câu 40:
Cho 3a ≤ 2b ( b ≥ 0 ). Hãy so sánh 2 số 5a và 4b
 Xem đáp án
Xem đáp án
Ta có: 3a ≤ 2b ⇒ 5/3.3a ≤ 5/3.2b ⇒ 5a ≤ 10/3b
Mà 10/3 < 4 ⇒ 10/3b ≤ 4b ⇒ 5a ≤ 4b
Câu 41:
Tìm tập nghiệm của các bất phương trình sau:
a) ( x + √ 3 )2 ≥ ( x - √ 3 )2 + 2
 Xem đáp án
Xem đáp án
a) Ta có: ( x + √ 3 )2 ≥ ( x - √ 3 )2 + 2
⇔ x2 + 2√ 3 x + 3 ≥ x2 - 2√ 3 x + 3 + 2
⇔ 4√ 3 x ≥ 2 ⇔ x ≥ (√ 3 )/6 → S = [ (√ 3)/6; + ∞ )
Vậy bất phương trình đã cho có tập nghiệm là S = [ (√ 3 )/6; + ∞ )
Câu 42:
b) x + √ x < ( 2√ x + 3 )( √ x - 1 )
 Xem đáp án
Xem đáp án
b) Ta có: x + √ x < ( 2√ x + 3 )( √ x - 1 )
Điều kiện: x ≥ 0
⇔ x + √ x < 2x - 2√ x + 3√ x - 3
⇔ - x < - 3 ⇔ x > 3
Kết hợp điều kiện, tập nghiệm bất phương trình là: S = ( 3; + ∞ )
Vậy bất phương trình đã cho có tập nghiệm là S = ( 3; + ∞ )
Câu 43:
c) ( x - 3 )√ (x - 2) ≥ 2
 Xem đáp án
Xem đáp án
c) Ta có: ( x - 3 )√ (x - 2) ≥ 2
Điều kiện: x ≥ 2
Bất phương trình tương đương là
Vậy tập nghiệm của bất phương trình là S = 2 ∪ [ 3; + ∞ )
Câu 44:
Có bao nhiêu giá trị thực của tham số m để bất phương trình ( m2 - m )x < m vô nghiệm là?
 Xem đáp án
Xem đáp án
Rõ ràng nếu
thì bất phương trình luôn có nghiệm.
Với m = 0, bất phương trình trở thành 0x < 0: vô nghiệm.
Với m = 1, bất phương trình trở thành 0x < 1: luôn đúng với mọi x ∈ R
Vậy với m = 0 thì bất phương trình trên vô nghiệm.
Câu 45:
Bỏ dấu giá trị tuyệt đối và rút gọn các biểu thức sau:
a) A = 3x + 2 + | 5x | với x > 0
 Xem đáp án
Xem đáp án
a) Với x > 0 ⇒ | 5x | = 5x
Khi đó ta có: A = 3x + 2 + | 5x | = 3x + 2 + 5x = 8x + 2
Vậy A = 8x + 2.
Câu 46:
b) A = | 4x | - 2x + 12 với x < 0.
 Xem đáp án
Xem đáp án
b) Ta có: x < 0 ⇒ | 4x | = - 4x
Khi đó ta có: A = | 4x | - 2x + 12 = - 4x - 2x + 12 = 12 - 6x
Vậy A = 12 - 6x.
Câu 47:
c) A = | x - 4 | - x + 1 với x < 4
 Xem đáp án
Xem đáp án
c) Ta có: x < 4 ⇒ | x - 4 | = 4 - x
Khi đó ta có: A = | x - 4 | - x + 1 = 4 - x - x + 1 = 5 - 2x.
Vậy A = 5 - 2x
Câu 48:
Giải các phương trình sau:
a) | 2x | = x - 6
 Xem đáp án
Xem đáp án
a) Ta có: | 2x | = x - 6
+ Với x ≥ 0, phương trình tương đương: 2x = x - 6 ⇔ x = - 6.
Không thỏa mãn điều kiện x ≥ 0.
+ Với x < 0, phương trình tương đương: - 2x = x - 6 ⇔ - 3x = - 6 ⇔ x = 2.
Không thỏa mãn điều kiện x < 0.
Vậy phương trình đã cho vô nghiệm.
Câu 49:
b) | - 5x | - 16 = 3x
 Xem đáp án
Xem đáp án
b) Ta có: | - 5x | - 16 = 3x
+ Với x ≥ 0, phương trình tương đương: 5x - 16 = 3x ⇔ 2x = 16 ⇔ x = 8
Thỏa mãn điều kiện x ≥ 0
+ Với x < 0, phương trình tương đương: - 5x - 16 = 3x ⇔ 8x = - 16 ⇔ x = - 2
Thỏa mãn điều kiện x < 0
Vậy phương trình đã cho có tập nghiệm là S = { - 2;8 }
Câu 50:
c) | 4x | = 2x + 12
 Xem đáp án
Xem đáp án
c) Ta có: | 4x | = 2x + 12
+ Với x ≥ 0, phương trình tương đương: 4x = 2x + 12 ⇔ 2x = 12 ⇔ x = 6
Thỏa mãn điều kiện x ≥ 0
+ Với x < 0, phương trình tương đương: - 4x = 2x + 12 ⇔ - 6x = 12 ⇔ x = - 2
Thỏa mãn điều kiện x < 0
Vậy phương trình đã cho có tập nghiệm là S = { - 2;6 }
Câu 51:
d) | x + 3 | = 3x - 1
 Xem đáp án
Xem đáp án
d) Ta có: | x + 3 | = 3x - 1
+ Với x ≥ - 3, phương trình tương đương: x + 3 = 3x + 1 ⇔ - 2x = - 2 ⇔ x = 1.
Thỏa mãn điều kiện x ≥ - 3
+ Với x < - 3, phương trình tương đương: - x - 3 = 3x + 1 ⇔ - 4x = 4 ⇔ x = - 1
Không thỏa mã điều kiện x < - 3
Vậy phương trình đã cho có tập nghiệm là S = { 1 }
Câu 52:
Giải bất phương trình với a là hằng số
 Xem đáp án
Xem đáp án
Điều kiện xác định: a ≠ 0.
Ta có:
⇔ x( a + 2 ) > 1/a ( 1 )
+ Nếu a > - 2,a ≠ 0 thì nghiệm của bất phương trình là
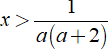
+ Nếu a < - 2 thì nghiệm của bất phương trình là
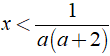
+ Nếu x = - 2 thì ( 1 ) có dạng 0x > - 1/2 luôn đúng với ∀ x ∈ R
Câu 53:
Tìm tất cả các giá trị của tham số m để bất phương trình mx + 4 > 0 nghiệm đúng với mọi | x | < 8 ?
 Xem đáp án
Xem đáp án
Yêu cầu của bài toán tương đương f( x ) = mx + 4 > 0, ∀ x ∈ ( - 8;8 )
⇔ Đồ thị hàm số y = f( x ) trên khoảng ( - 8;8 ) nằm phía trên trục hoành
⇔ Hai đầu mút của đoạn thẳng đó đều nằm trên phía trục hoành
Vậy giá trị m cần tìm là m ∈ [ - 1/2;1/2 ]
Câu 54:
Tìm giá trị nhỏ nhất của biểu thức N = x( x + 1 )( x + 2 )( x + 3 )
 Xem đáp án
Xem đáp án
Ta có: N = ( x2 + 3x )( x2 + 3x + 2 )
Đặt y = x2 + 3x2, ta đưa biểu thức về dạng:
N = y( y + 2 ) = y2 + 2y + 1 - 1 = ( y + 1 )2 - 1 ≥ - 1
Dấu bằng xảy ra khi và chỉ khi y + 1 = 0 ⇔ y = - 1 tức x2 + 3x = - 1
Ta có: x2 + 3x = - 1 ⇔ x2 + 3x + 1 = 0
Vậy giá trị nhỏ nhất là
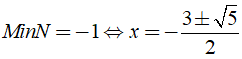
Câu 55:
Giải phương trình | x - 5 | + | x + 3 | = 3x - 1
 Xem đáp án
Xem đáp án
+ Với x < - 3, phương trình đã cho có dạng:
( 5 - x ) - ( x + 3 ) = 3x - 1 ⇔ x = 3/5 (loại vì không thỏa mãn điều kiện)
+ Với - 3 ≤ x < 5, phương trình đã cho có dạng:
( 5 - x ) + ( x + 3 ) = 3x - 1 ⇔ 3x = 9 ⇔ x = 3 (thỏa mãn khoảng đang xét)
+ Với x ≥ 5, phương trình đã cho có dạng:
( x - 5 ) + ( x + 3 ) = 3x - 1 ⇔ x = - 1 (không thỏa mãn không xét)
Vậy phương trình đã cho có nghiệm là x = 3
