8 câu hỏi trắc nghiệm thuộc Đề thi Giữa kì 1 Toán lớp 8 có đáp án (Đề 2)

Đề thi Giữa kì 1 Toán lớp 8 có đáp án

Đề thi Giữa kì 1 Toán lớp 8 có đáp án (Đề 2)

2281 lượt thi
8 câu hỏi
30 phút

Danh sách câu hỏi

Câu 1:

x^{2} - 6 x + 9

tại

x = - 3

là:

A. -6

B. 6

C. 36

D. -36

Xem đáp án

Đáp án: C

Câu 2:

Câu 2: Kết quả phép tính $- 2 x^{2} . (2 - x)$ là:

A. $4 x^{2} - 2 x^{3} .$

B. $2 x^{3} - 4 x^{2} .$

C. $- 2 x^{3} + 4 x^{2} .$

D. $- 2 x^{2} .$

Xem đáp án

Đáp án: B

Câu 3:

Câu 3: Nếu $x^{3} + x$ thì tập giá trị của x là:

A. $\{0; - 1; 1\} .$

B. $\{- 1; 1\} .$

C. $\{0; 1\} .$

D. $\{0\} .$

Xem đáp án

Đáp án: D

Câu 4:

Câu 4: Một hình thang có một cặp góc đối là: $125 °$ và $65 ° .$ Cặp góc đối còn lại của hình đó là:

A. $105 °, 45 ° .$

B. $105 °, 65 ° .$

C. $55 °, 115 ° .$

D. $115 °, 65 ° .$

Xem đáp án

Đáp án: C

Câu 5:

a. Làm tính nhân: $5 x (6 x^{2} - x + 3)$

b. Tính nhanh: $85 .12, 7 + 15 .12, 7$

Xem đáp án

a. $5 x . (6 x^{2} - x + 3) = 5 x . 6 x^{2} + 5 x . (- x) + 5 x . 3$ $= 30 x^{3} - 5 x^{2} + 15 x$

b. $85 .12, 7 + 15 .12, 7 = 12, 7 . (85 + 15)$ $= 12, 7 .100 = 1270$

Câu 6:

a. Phân tích đa thức sau thành nhân tử: $xy - x^{2} + x - y$

b. Tìm a để đa thức $x^{4} - 3 x^{3} - 6 x + a$ chia hết cho đa thức $x^{2} - 3 x - 2 .$

Xem đáp án

a. $xy - x^{2} + x - y = - x (x - y) + (x - y)$ $= (x - y) (1 - x)$

b. Sắp xếp và đặt phép tính chia theo cột đúng

$\begin{array}{l} \begin{array}{l} x^{4} - 3 x^{3} - 6 x + a \\ _________________ \end{array}| \frac{x^{2} - 3 x + 2}{x^{2} + 2} \\ x^{4} - 3 x^{3} - 2 x^{2} \\ \underline{2 x^{2} - 6 x + a} \end{array}$

$x^{4} - 3 x^{3} - 6 x + a = (x^{2} - 3 x - 2) (x^{2} + 2) + a + 4$

Để đa thức $x^{4} - 3 x^{3} - 6 x + a$ chia hết cho đa thức

$x^{2} - 3 x - 2$ thì $a + 4 = 0 \Rightarrow a = - 4$

Vậy đa thức $x^{4} - 3 x^{3} - 6 x + a$ chia hết cho đa thức $x^{2} - 3 x - 2$ khi $a = - 4$

Câu 7:

Câu 7: Cho tam giác $ABC (AB < AC),$ đường cao AH. Gọi $D, E, F$ lần lượt là trung điểm của các cạnh $AB, AC, BC .$

a) Chứng minh rằng tứ giác $BDEF$ là hình bình hành.

b) Chứng minh tứ giác $EFHD$ là hình thang cân.

c) Biết số đo góc $B = 60 °$ . Hãy tính các góc của tứ giác $EFHD .$

Xem đáp án

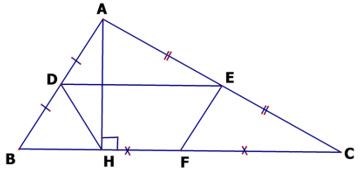
Ta có:

$AD = DB$ (gt)

$AE = EC$ (gt)

$\Rightarrow DE$ là đường trung bình của $ΔABC$

$\Rightarrow DE // BC$ mà F thuộc $BC \Rightarrow DE / / BF (1)$

Chứng minh tương tự có: $EF / / BD (2)$

từ (1) và (2) $\Rightarrow BDEF$ là hình bình hành

Vì HD là đường trung tuyến ứng với cạnh huyền trong $ΔAHB$ vuông tại $H \Rightarrow BD = HD = AB$

$\Rightarrow ΔHBD$ cân tại D

$\Rightarrow$ Góc BDH = góc DHB (3)

mặt khác góc HDE = góc DHB (sole trong do $DE / / BC$ (4)

Từ (3) và (4) ta có: góc HDE = góc FED

Xét tứ giác HDEF có góc HDE = góc FED

$\Rightarrow$ Tứ giác EFHD là hình thang cân

Vì tứ giác EFHD là hình thang cân nên

góc HDE = góc FED = góc $B = 60 °$

HS tính được góc DHF = góc EFH $= 120 °$

Câu 8:

Câu 8: Chứng minh rằng: Tích của 4 số tự nhiên liên tiếp cộng với 1 là một số chính phương.

Xem đáp án

Gọi 4 số tự nhiên liên tiếp lần lượt là $n; n + 1; n + 2; n + 3$

Tích của 4 số tự nhiên liên tiếp là: $n (n + 1) (n + 2) (n + 3)$

Tích của 4 số tự nhiên liên tiếp cộng với 1 là:

$\begin{array}{l} n (n + 1) (n + 2) (n + 3) + 1 = (n^{2} + 3 n) (n^{2} + 3 n + 2) + 1 \end{array}$

$= {(n^{2} + 3 n)}^{2} + 2 (n^{2} + 3 n) + 1$

$= {(n^{2} + 3 n + 1)}^{2}$ là một số chính phương

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề thi Giữa kì 1 Toán lớp 8 có đáp án

Đề thi Giữa kì 1 Toán lớp 8 có đáp án (Đề 2)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương