Trắc nghiệm Toán 10 (có đáp án): Phương trình chưa dấu giá trị tuyệt đối
-
506 lượt thi
-
34 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Phương trình có nghiệm duy nhất khi:
 Xem đáp án
Xem đáp án
Điều kiện:
Phương trình
Phương trình (1) có nghiệm duy nhất khác -1
Đáp án cần chọn là: C
Câu 2:
Phương trình vô nghiệm khi:
 Xem đáp án
Xem đáp án
Điều kiện:
Phương trình
Phương trình (1) vô nghiệm ⇔ Phương trình (2) vô nghiệm hoặc có nghiệm duy nhất
Vậy
Đáp án cần chọn là: A
Câu 3:
Tập nghiệm của phương trình là:
 Xem đáp án
Xem đáp án
Điều kiện:
Phương trình:
Vậy
Đáp án cần chọn là: C
Câu 5:
Tập nghiệm của phương trình trường hợp là:
 Xem đáp án
Xem đáp án
Điều kiện:
Phương trình thành
Vì suy ra
Đáp án cần chọn là: A
Câu 6:
Tập nghiệm S của phương trình trong trường hợp là:
 Xem đáp án
Xem đáp án
Dễ thấy nên
Đáp án cần chọn là: D
Câu 7:
Phương trình có nghiệm duy nhất khi:
 Xem đáp án
Xem đáp án
Điều kiện:
Phương trình (1) trở thành
Phương trình (1) có nghiệm duy nhất
⇔ Phương trình (2) có nghiệm duy nhất khác −1 và 1
Đáp án cần chọn là: C
Câu 8:
Gọi S là tập hợp các giá trị nguyên của tham số m thuộc đoạn [−3;5] để phương trình có nghiệm. Tổng các phần tử trong tập S bằng:
 Xem đáp án
Xem đáp án
Phương trình đã cho có nghiệm
Vì m ∈ Z, m ∈ [−3; 5] nên m ∈ S = {−3; −2; 1; 2; 3; 4; 5}.
Đáp án cần chọn là: D
Câu 9:
Biết phương trình có nghiệm duy nhất và nghiệm đó là nghiệm nguyên. Vậy nghiệm đó là:
 Xem đáp án
Xem đáp án
Điều kiện:
Phương trình (1) thành:
Phương trình (1) có nghiệm duy nhất.
⇔ Phương trình (2) có nghiệm duy nhất khác 1 hoặc phương trình (2) có 2 nghiệm phân biệt có một nghiệm bằng 1
Với phương trình có nghiệm là
Với phương trình có nghiệm là
Với a = -1 phương trình có nghiệm là:
Đáp án cần chọn là: D
Câu 10:
Có bao nhiêu giá trị của tham số m để phương trình vô nghiệm?
 Xem đáp án
Xem đáp án
Ta có:
Phương trình đã cho vô nghiệm
Đáp án cần chọn là: D
Câu 11:
Phương trình |ax + b| = |cx + d| tương đương với phương trình:
 Xem đáp án
Xem đáp án
Ta có:
Đáp án cần chọn là: C
Câu 12:
Phương trình |ax + b| = cx + d tương đương với phương trình:
 Xem đáp án
Xem đáp án
Ta có:
Đáp án cần chọn là: C
Câu 14:
Tổng các nghiệm của phương trình bằng:
 Xem đáp án
Xem đáp án
Phương trình
Do đó, tổng các nghiệm của phương trình bằng
Đáp án cần chọn là: D
Câu 17:
Tổng các nghiệm của phương trình bằng:
 Xem đáp án
Xem đáp án
Ta có:
Dấu “=” xảy ra khi và chỉ khi
Đáp án cần chọn là: B
Câu 18:
Phương trình có bao nhiêu nghiệm?
 Xem đáp án
Xem đáp án
Ta có: |2x − 4| − 2x + 4 = 0
Đáp án cần chọn là: D
Câu 21:
Gọi là hai nghiệm của phương trình . Tính giá trị biểu thức
 Xem đáp án
Xem đáp án
Phương trình
Đáp án cần chọn là: C
Câu 22:
Tập nghiệm của phương trình là:
 Xem đáp án
Xem đáp án
Điều kiện:
Phương trình (1) trở thành:
TH1:
Phương trình thành
TH2:
Phương trình thành
Vậy
Đáp án cần chọn là:C
Câu 23:
Tập nghiệm của phương trình là:
 Xem đáp án
Xem đáp án
Điều kiện:
Ta có:
Vậy S = {5}.
Đáp án cần chọn là: D
Câu 24:
Cho . Với m là bao nhiêu thì (1) có nghiệm duy nhất
 Xem đáp án
Xem đáp án
Điều kiện
, phương trình luôn có nghiệm là và
Phương trình (1) có duy nhất 1 nghiệm
Đáp án cần chọn là: D
Câu 25:
Với giá trị nào của tham số a thì phương trình: có hai nghiệm phân biệt
 Xem đáp án
Xem đáp án
Điều kiện:
Phương trình thành
+) Nếu thì phương trình có ba nghiệm phân biệt , , nên không thỏa mãn yêu cầu.
+) Nếu thì do điều kiện nên ta loại nghiệm , do đó phương trình có hai nghiệm phân biệt , (thỏa mãn)
+) Nếu thì phương trình có nghiệm duy nhất (không thỏa mãn).
+) Nếu thì do điều kiện nên ta loại hai nghiệm , , do đó phương trình có nghiệm duy nhất (không thỏa mãn)
Vậy phương trình có 2 nghiệm phân biệt
Đáp án cần chọn là: B
Câu 26:
Phương trình: , có nghiệm là:
 Xem đáp án
Xem đáp án
Trường hợp 1: x < −2
Phương trình thành:
Trường hợp 2:
Phương trình thành:
Trường hợp 3: x > 3
Phương trình thành:
Vậy
Đáp án cần chọn là: D
Câu 27:
Phương trình: có nghiệm là:
 Xem đáp án
Xem đáp án
Điều kiện:
Phương trình thành:
TH 1: x < −1
Phương trình thành:
TH 2: −1 ≤ x ≤ 0
Phương trình thành:
TH3: x > 0
Phương trình thành:
Đáp án cần chọn là: D
Câu 28:
Tổng các nghiệm của phương trình bằng:
 Xem đáp án
Xem đáp án
Phương trình tương đương với
Đặt . Suy ra
Phương trình trở thành
Với , ta có
Đáp án cần chọn là: B
Câu 29:
Phương trình có bao nhiêu nghiệm?
 Xem đáp án
Xem đáp án
Đặt
Phương trình trở thành
- Với ta có | hoặc
- Với ta có hoặc hoặc
Vậy phương trình có bốn nghiệm là , , , .
Đáp án cần chọn là: D
Câu 30:
Tập nghiệm T của phương trình: là:
 Xem đáp án
Xem đáp án
Điều kiện: x > 4
Phương trình trở thành:
Vậy T = (4; +∞).
Đáp án cần chọn là: C
Câu 31:
Phương trình: có 1 nghiệm duy nhất khi và chỉ khi:
 Xem đáp án
Xem đáp án
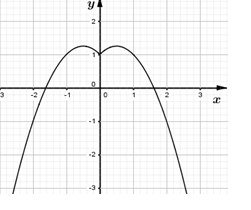
Biểu diễn đồ thị hàm số f(x) lên hệ trục tọa độ như hình vẽ bên trên:
+ Vẽ đồ thị hàm số
+ Giữ nguyên nhánh đồ thị bên phải trục tung và lấy đối xứng nó qua trục tung.
+ Xóa bỏ phần bên trái trục tung trước đó đi.
Dựa vào đồ thị ta suy ra không tồn tại m để phương trình có duy nhất 1 nghiệm.
Đáp án cần chọn là: D
Câu 32:
Với giá trị nào của a thì phương trình có nghiệm duy nhất?
 Xem đáp án
Xem đáp án
Dễ thấy, không là nghiệm của phương trình đã cho.
- Xét :
Phương trình trở thành
Phương trình (1) có nghiệm duy nhất khi
Khi đó, nghiệm của phương trình là . Mà
- Xét x ∈ (0; +∞):
Phương trình trở thành
Phương trình (2) có nghiệm duy nhất khi
Khi đó, nghiệm của phương trình là . Mà
Đáp án cần chọn là: D
Câu 33:
Phương trình: , có nghiệm là:
 Xem đáp án
Xem đáp án
Trường hợp 1:
Phương trình thành:
Trường hợp 2:
Phương trình thành:
Suy ra:
Trường hợp 3:
Phương trình thành:
Trường hợp 4:
Phương trình thành:
Vậy
Đáp án cần chọn là: A
Câu 34:
Phương trình có nghiệm là:
 Xem đáp án
Xem đáp án
Ta có: ;
Từ đó ta phá dấu giá trị tuyệt đối của mỗi biểu thức như sau:
TH1:
Phương trình thành:
TH2: 1 < x < 2
Phương trình thành:
TH3:
Phương trình thành:
TH4: 3 < x < 4
Phương trình thành:
TH5:
Phương trình thành:
Đáp án cần chọn là: D
