Bài tập theo tuần Toán 8 - tuần 20
-
5979 lượt thi
-
21 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Cho hai phương trình:
a) Chứng minh rằng phương trình có nghiệm chung là
b) Chứng minh rằng là nghiệm của (1) nhưng không là nghiệm của (2). Hai phương trình đã cho có tương đương với nhau không ? Vì sao ?
 Xem đáp án
Xem đáp án
a)a) Thay vào phương trình (1), phương trình (2) ta có:
Vậy là nghiệm chung của 2 phương trình
b) Thay vào phương trình (1)
Vậy là nghiệm của phương trình (1) nhưng không là nghiệm của phương trình (2). Vậy hai phương trình đã cho không tương đương do không có chung tập nghiệm
Câu 2:
Chứng tỏ rằng hai phương trình sau không tương đương :
và
 Xem đáp án
Xem đáp án
Phương trình có TXĐ:
Còn phương trình có nên hai phương trình không tương đương.
Câu 3:
Cho hai phương trình :
Xác định m để hai phương trình trên tương đương Xem đáp án
Xem đáp án
Để hai phương trình tương đương là nghiệm
Câu 9:
Cho hình chữ nhật có diện tích là và tỉ số các cạnh là . Tính chu vi hình chữ nhật đó
 Xem đáp án
Xem đáp án
Gọi chiều rộng 4a : Chiều dài : 9a
Vậy chu vi hình chữ nhật:
Câu 10:
 Xem đáp án
Xem đáp án
Phương trình có nghiệm bằng 1 , thay vào phương trình
Câu 11:
 Xem đáp án
Xem đáp án
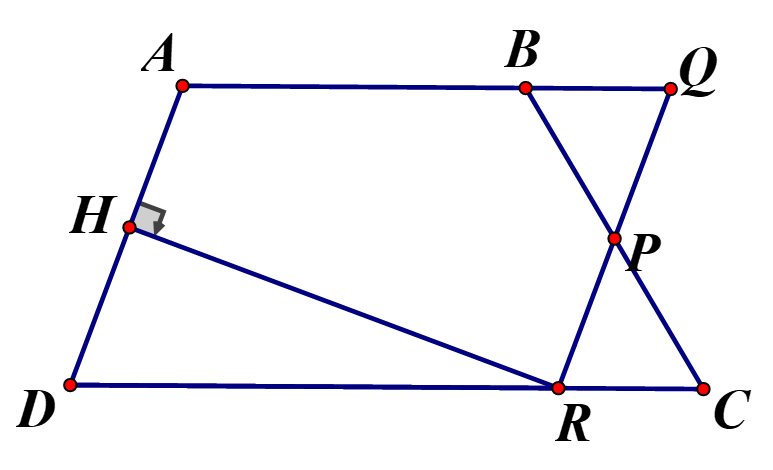
a) Xét có : là hình bình hành
Nên
b) Xét và có:
(so le trong), (đối đỉnh)
Vậy
