Bài tập theo tuần Tuần 8 - Tuần 22
-
5984 lượt thi
-
29 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 5:
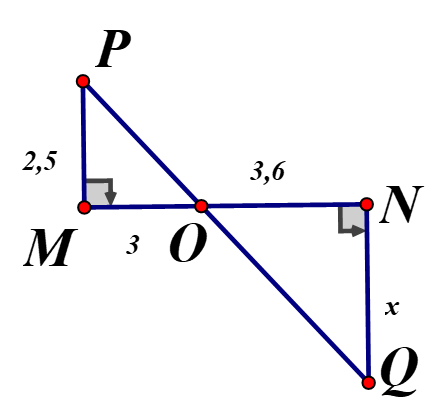
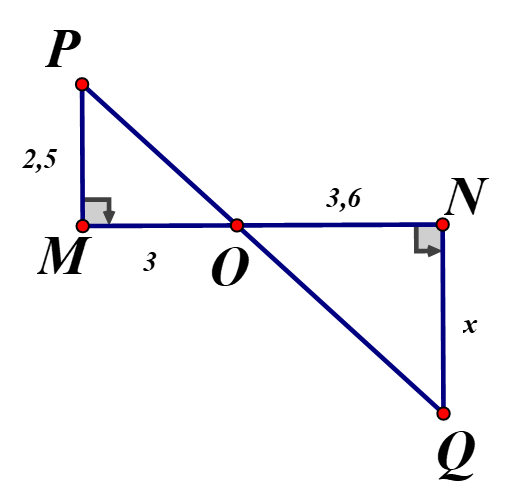
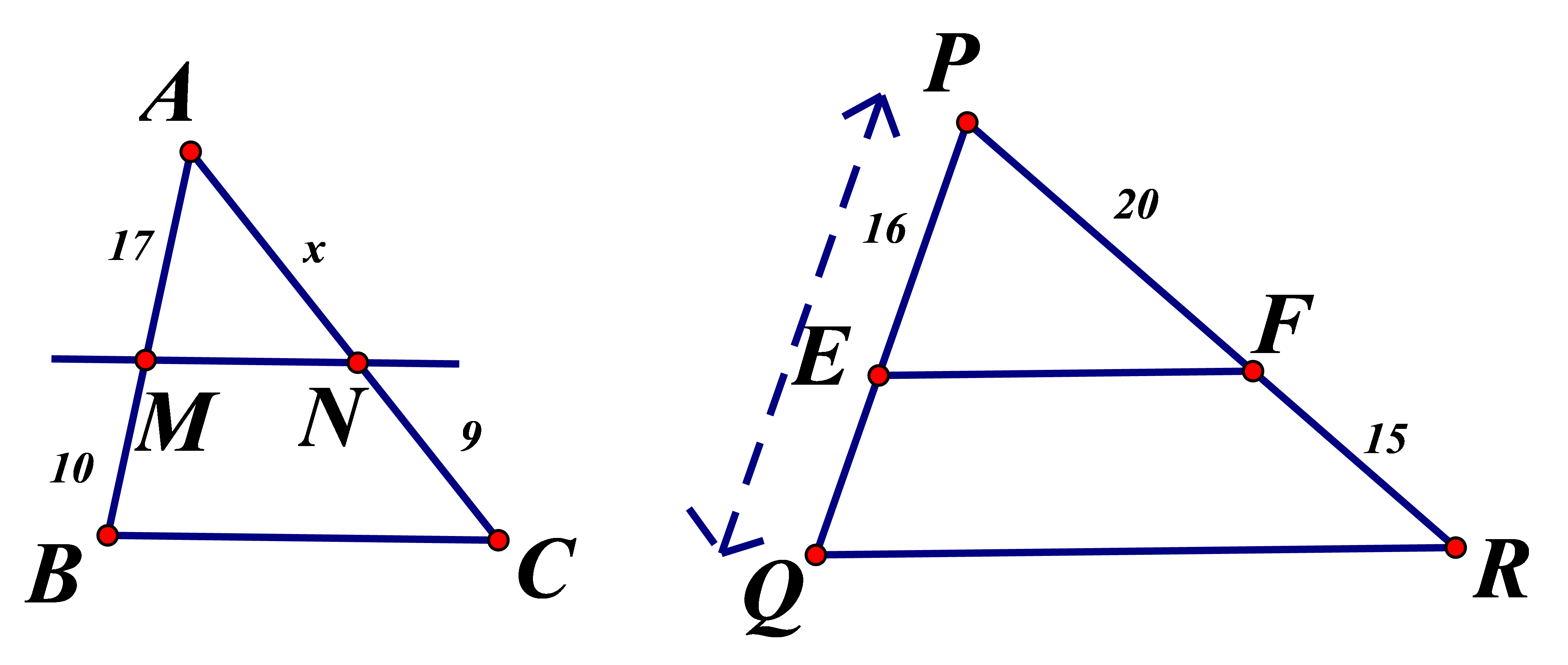
Tính độ dài x trong các hình sau : biết MN//BC, EF// QR
 Xem đáp án
Xem đáp án
Vì Áp dụng định lý Ta let
hay
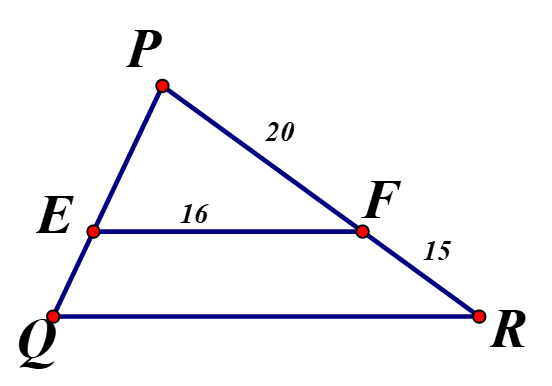
Vì , áp dụng định lý Ta – let
Câu 7:
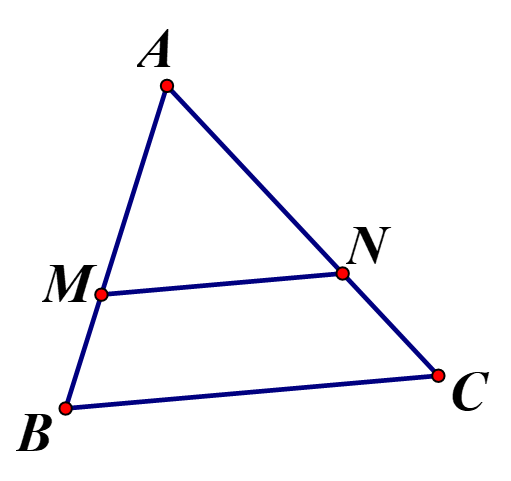
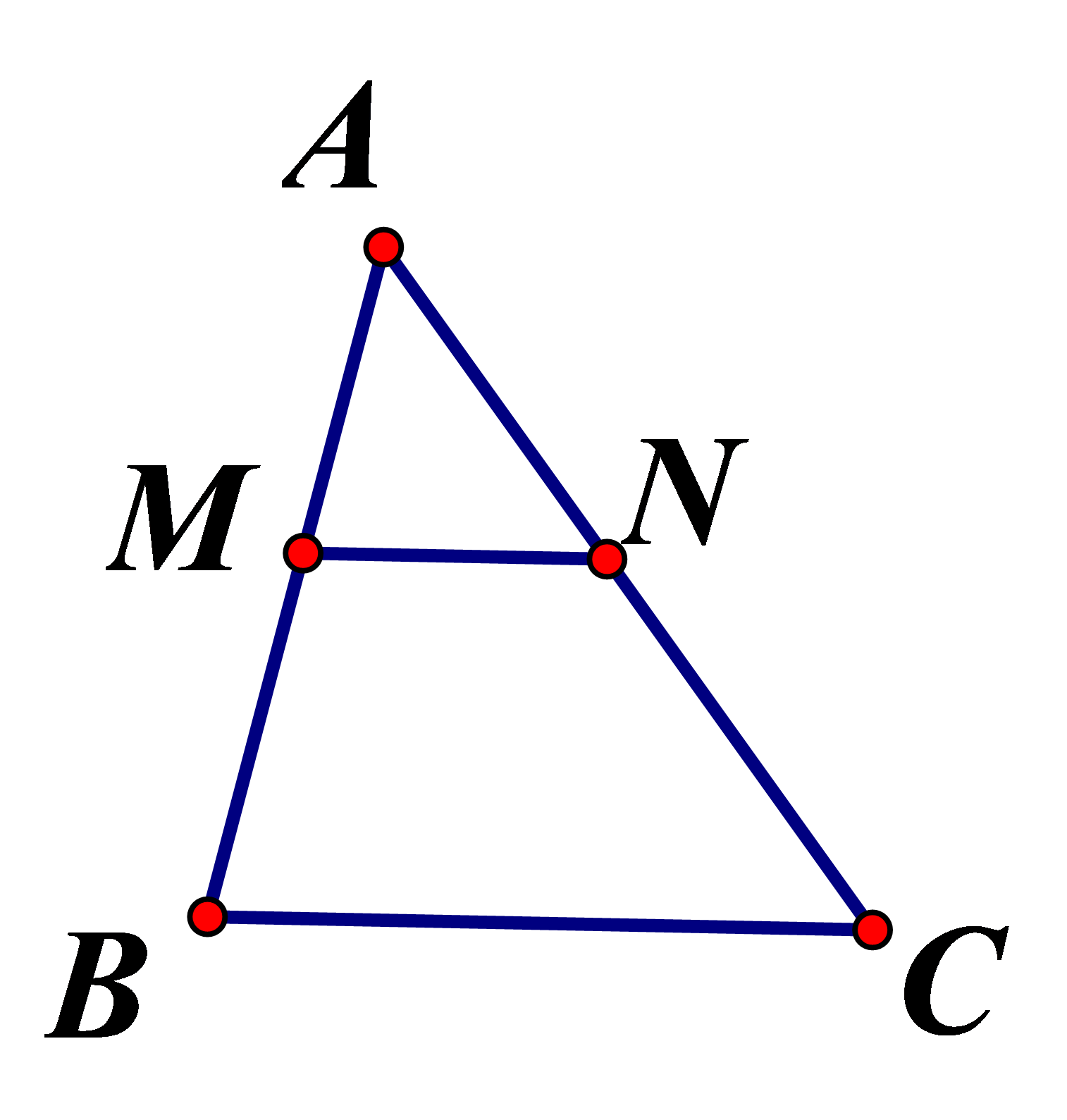
Cho hình vẽ
Cho MN//BC
a) Vận dụng định lý Ta – lét , viết các hệ thức b) Biết AM=5cm, MB=10cm, MN=7cm. Tính BC
 Xem đáp án
Xem đáp án
a) Vì , áp dụng định lý Ta let:
Ta có : hayCâu 8:
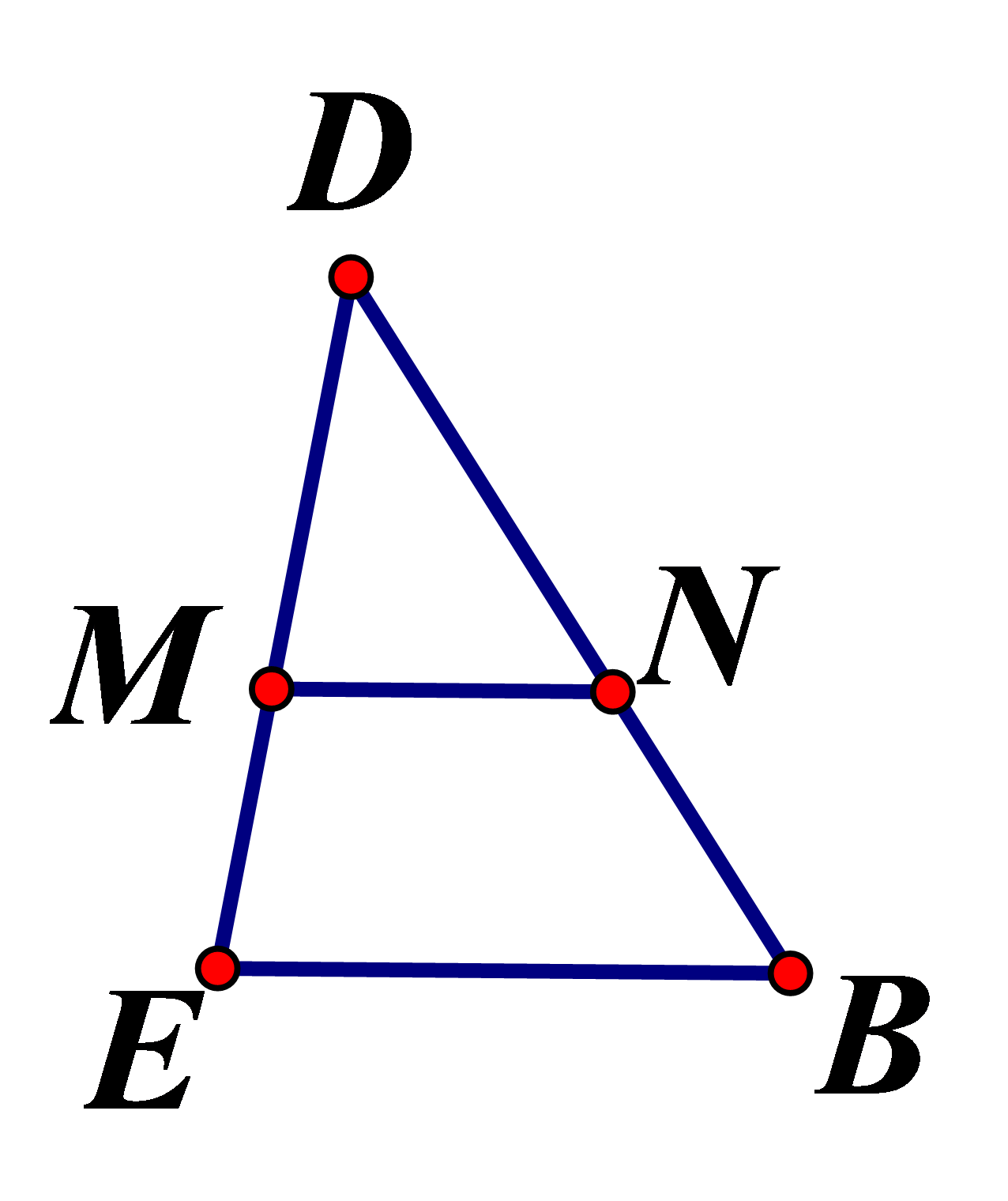
Cho hình vẽ, biết MN//BE,
a) Dùng định lý Talet, hãy viết các đoạn thẳng tỉ lệ
b)Tính MN biết DE=16cm, MD=4cm, BE=24cm
 Xem đáp án
Xem đáp án
a) Vì áp dụng định lý Ta let:
b) Vì áp dụng hệ quả Ta let
hay
Câu 9:
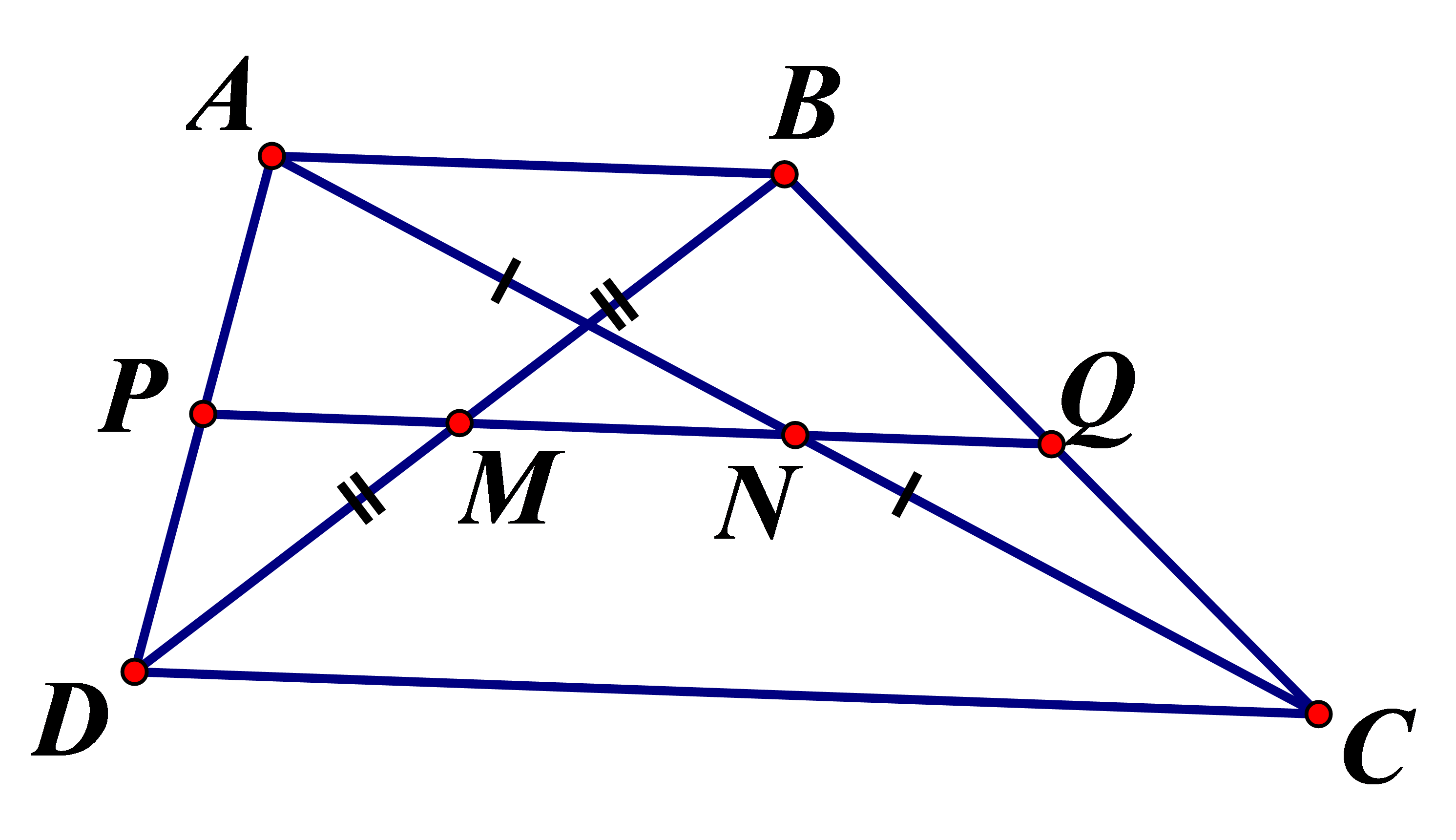
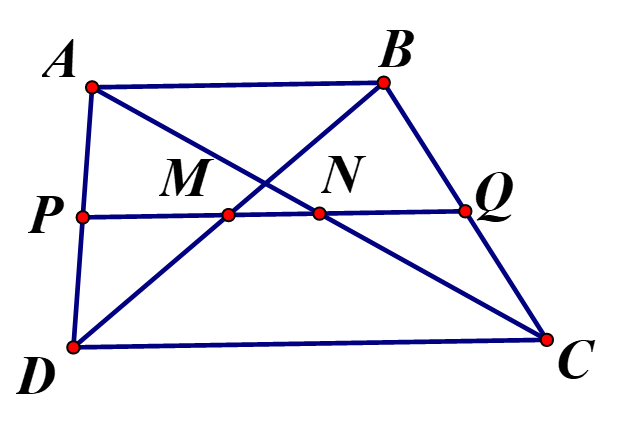
Cho hình thang ABCD có AB//CD (AB<CD) trung điểm của các đường chéo AC,BD là N,M (như hình). Chứng minh rằng:
 Xem đáp án
Xem đáp án
a. Gọi P là trung điểm của là trung điểm của AD, M là đường trung bình DB nên PM là đường trung bình của tam giác ADB, nên PM//AB, mà N là trung điểm AC, suy ra PN là đường trung bình thẳng hàng
b) Gọi Q là trung điểm BC, cmtt câu a , Suy ra M, N, P thẳng hàng
Câu 10:
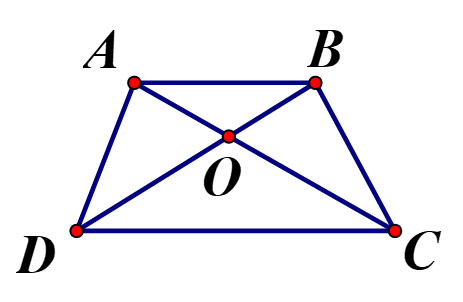
Hình thang ABCD có hai đường chéo AC, BD cắt nhau tại O. Chứng minh rằng OA.OD=OB.OC
 Xem đáp án
Xem đáp án
Xét hình thang ABCD, có AB//CD Áp dụng hệ quả Ta let
Câu 16:
Giải phương trình (x-6)4+(x-8)4=16
 Xem đáp án
Xem đáp án
Đặt phương trình thành:
Đặt
Phương trình thành:
Theo bất đẳng thức Cô si
Dấu xảy ra
Thay vào (*)