23 câu hỏi trắc nghiệm thuộc Bài tập theo tuần Toán 8 - Tuần 23

Câu 1:

$\frac{5 x}{x + 1} + 1 = \frac{- 6}{x + 1}$

$\begin{array}{l} \frac{5 x}{x + 1} + 1 = \frac{- 6}{x + 1} (x \neq - 1) \Leftrightarrow \frac{5 x + x + 1}{x + 1} = \frac{- 6}{x + 1} \\ \Rightarrow 6 x + 1 = - 6 \Leftrightarrow x = \frac{- 7}{6} (t m) . S = \{\frac{- 7}{6}\} \end{array}$

$\begin{array}{l} \end{array}$

Câu 2:

Giải các phương trình chứa ẩn ở mẫu sau :

$\begin{array}{l} \frac{1}{x + 1} - \frac{5}{x - 2} = \frac{15}{(x + 1) (2 - x)} \end{array}$

Xem đáp án

$\begin{array}{l} \frac{1}{x + 1} - \frac{5}{x - 2} = \frac{15}{(x + 1) (x - 2)} (\begin{array}{l} x \neq - 1 \\ x \neq 2 \end{array}) \\ \Leftrightarrow \frac{x - 2 - 5 x - 5}{(x + 1) (x - 2)} = \frac{15}{(x + 1) (x - 2)} \Leftrightarrow - 4 x = 15 + 7 \Leftrightarrow x = - \frac{11}{2} (t m) \end{array}$

Câu 3:

Cho hai biểu thức

$A = \frac{5}{2 m + 1}$ ) và

$B = \frac{4}{2 m - 1}$ . Hãy tìm m để hai biểu thức ấy có giá trị thỏa mãn hệ thức :

a) 2A+3B=0

b) AB=A+B

Xem đáp án

$\begin{array}{l} a) 2 A + 3 B = 0 \Leftrightarrow 2. \frac{5}{2 m + 1} + 3. \frac{4}{2 m - 1} = 0 (m \neq \pm \frac{1}{2}) \\ \Leftrightarrow \frac{10 (2 m - 1) + 12 (2 m - 1)}{(2 m + 1) (2 m - 1)} = 0 \\ \Rightarrow 20 m - 10 + 24 m - 12 = 0 \Leftrightarrow m = \frac{1}{2} (k t m) \end{array}$

Vậy không có giá trị của để 2A+3B=0

$\begin{array}{l} b) A B = A + B \\ \Leftrightarrow \frac{5}{2 m + 1} . \frac{4}{2 m - 1} = \frac{5}{2 m + 1} + \frac{4}{2 m - 1} (m \neq \pm \frac{1}{2}) \\ \Leftrightarrow \frac{20}{(2 m + 1) (2 m - 1)} = \frac{5 (2 m - 1) + 4 (2 m + 1)}{(2 m + 1) (2 m - 1)} \\ \Rightarrow 20 = 10 m - 5 + 8 m + 4 \Leftrightarrow m = \frac{7}{6} (t m) \end{array}$

Vậy $m = \frac{7}{6}$ thì $A B = A + B$

Câu 4:

Giải các phương trình sau :

$\begin{array}{l} \frac{3 x - 1}{x - 1} - \frac{2 x + 5}{x + 3} = 1 - \frac{4}{(x - 1) (x + 3)} \end{array}$

Xem đáp án

$\begin{array}{l} \frac{3 x - 1}{x - 1} - \frac{2 x + 5}{x + 3} = 1 - \frac{4}{(x - 1) (x + 3)} (\begin{array}{l} x \neq 1 \\ x \neq - 3 \end{array}) \\ \Leftrightarrow \frac{(3 x - 1) (x + 3) - (2 x + 5) (x - 1)}{(x - 1) (x + 3)} = \frac{(x - 1) (x + 3) - 4}{(x - 1) (x + 3)} \\ \Rightarrow 3 x^{2} + 8 x - 3 - 2 x^{2} - 3 x + 5 = x^{2} + 2 x - 3 - 4 \\ \Leftrightarrow 3 x = - 9 \Leftrightarrow x = - 3 (k t m) S = \emptyset \end{array}$

Câu 5:

Cho $Δ A B C$

a) Vẽ đường phân giác AM của Góc A

b) Viết các đoạn thẳng tỉ lệ.

c) Biết $A B = 5 c m, A C = 8,5 c m, M B = 3 c m .$ Tính BC

Xem đáp án

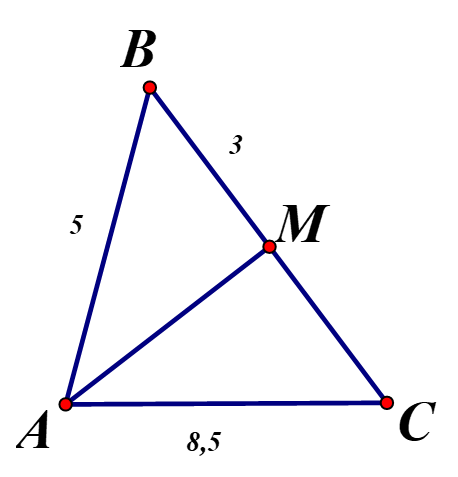
Cho tam giác ABC a) Vẽ đường phân giác AM của góc A b) Viết các đoạn thẳng tỉ lệ. c) Biết AB=5cm. AC=8,5cm Tính BC (ảnh 1)

b) $Δ A B C$ có AM là đường phân giác nên $\frac{A B}{A C} = \frac{M B}{M C}$ (tính chất đường phân giác trong tam giác)

c) Ta có: $\frac{A B}{A C} = \frac{M B}{M C} (c m t) h a y \frac{5}{8,5} = \frac{3}{M C} \Leftrightarrow M C = 5,1 (c m)$

$\Rightarrow B C = B M + M C = 3 + 5,1 = 8,1 (c m)$

Câu 6:

Cho $Δ A B C$ có $A C = 8 c m, B C = 10 c m .$ Gọi CE là phân giác của góc C

a) Cho biết $E B = 7 c m .$ Tính AE

b) Cho biết $A E . E B = 80.$ Tính AB

Xem đáp án

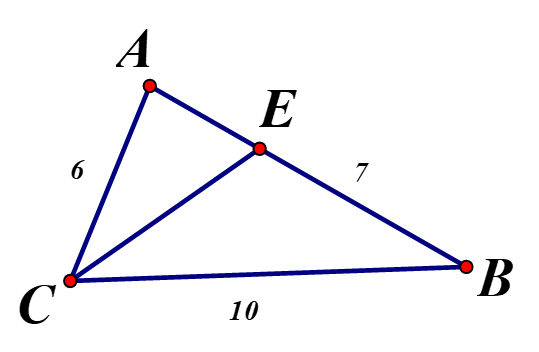
Cho tam giác ABC có AC=8cm, BC=10cm Gọi CE là phân giác của góc C a) Cho biết EB=7cm Tính AE (ảnh 1)

Vì CE là đường phân giác của $Δ A C B \Rightarrow \frac{A E}{E B} = \frac{A C}{B C}$ (tính chất đường phân giác tam giác) hay $\frac{A E}{7} = \frac{8}{10} \Rightarrow A E = 5,6 c m$

b) Ta có: $A E . E B = 80 h a y 5,6. E B = 80 \Leftrightarrow E B = 14 \frac{2}{7} (c m)$

$\Rightarrow A B = A E + E B = 5,6 + 14 \frac{2}{7} = \frac{695}{35} (c m)$

Câu 7:

Cho tam giác $A B C (∠ A = 90^{0}), A B = 21 c m, A C = 28 c m .$ Đường phân giác góc A cắt tại D, đường thẳng qua và song song với AB, cắt AC tại E.

a) Tính độ dài $B D, D C, D E$

b) Tính $S_{A B D}, S_{A C D}$

Xem đáp án

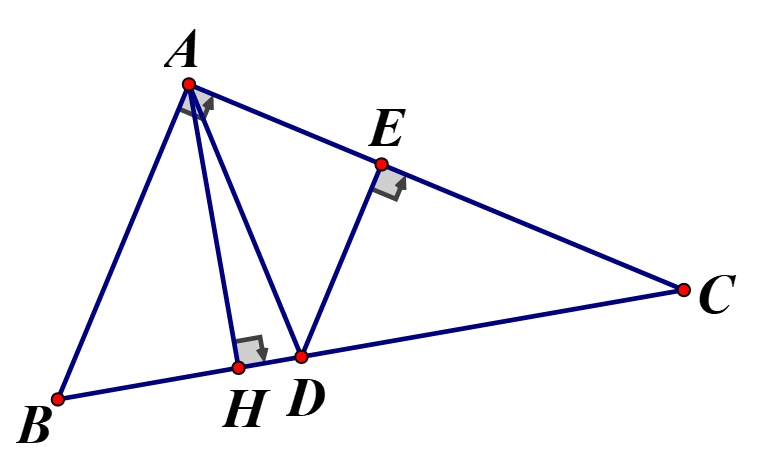
Cho tam giác ABC ( góc A=90 độ) Đường phân giác góc A cắt BC tại D, đường thẳng qua D và song song với AB cắt AC tại E. (ảnh 1)

a) Áp dụng định lý Pytago vào vuông tại A

$\Rightarrow B C = \sqrt{21^{2} + 28^{2}} = 35 (c m)$

Vì là tia phân giác của góc A nên $\frac{B D}{D C} = \frac{A B}{A C}$

$\Rightarrow \frac{B D + D C}{B D} = \frac{A B + A C}{A C}$ (dãy tỉ số bằng nhau)

$\Leftrightarrow \frac{B C}{B D} = \frac{A B + A C}{A C}$ hay $\frac{35}{B D} = \frac{21 + 28}{28} \Leftrightarrow B D = 20 (c m)$

$\Rightarrow D C = B C - B D = 35 - 20 = 15 (c m)$

Ta có: $D E / / B C (g t) \Rightarrow \frac{D E}{A B} = \frac{C D}{B C}$ (hệ quả Ta let)

Hay $\frac{D E}{21} = \frac{15}{35} \Rightarrow D E = 9 (c m)$

Vậy $B D = 20 c m, D C = 15 c m, D E = 9 c m$

b) Kẻ $A H ⊥ B C$ . Ta có:

$\begin{array}{l} S_{A B C} = \frac{A B . A C}{2} = \frac{B C . A H}{2} \Rightarrow A H = \frac{A B . A C}{B C} = 16,8 (c m) \\ S_{A B D} = \frac{A H . B D}{2} = \frac{16,8.20}{2} = 168 (c m^{2}) \\ S_{A C D} = \frac{C D . A H}{2} = \frac{15.16,8}{2} = 126 (c m^{2}) \end{array}$

Câu 8:

Tam giác ABC có $∠ A = 90^{0}, A B = 12 c m, A C = 16 c m .$ Đường phân giác góc A cắt BC tại D.

a) Tính $B C, B D, C D$

b) Vẽ đường cao AH. Tính $A H, H D, A D$

Xem đáp án

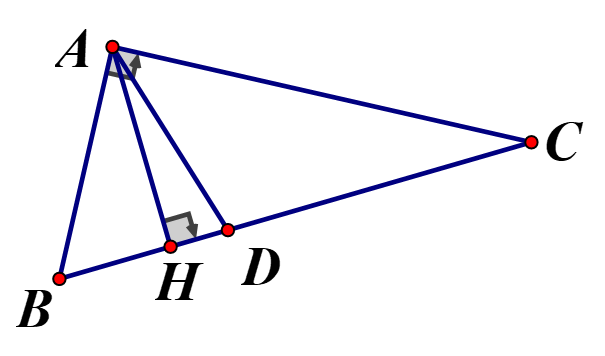
Tam giác ABC có góc A =90 độ, AB=12cm, AC=16cm. Đường phân giác góc A cắt BC tại D. a) Tính BC,BD,CD (ảnh 1)

a) Vì $Δ A B C$ vuông tại A nên $B C^{2} = \sqrt{A B^{2} + A C^{2}} (p y t a g o) = \sqrt{12^{2} + 16^{2}} = 20 (c m)$

Vì là phân giác của

$\Rightarrow \frac{B D}{D C} = \frac{A B}{A C}$ (tính chất đường phân giác của

$\Rightarrow \frac{A B + A C}{A C} = \frac{B D + D C}{D C}$ (tính chất dãy tỉ số bằng nhau)

$\begin{array}{l} \Rightarrow \frac{A B + A C}{A C} = \frac{B C}{D C} h a y \frac{12 + 16}{12} = \frac{20}{D C} \Rightarrow D C = \frac{80}{7} (c m) \\ \Rightarrow B D = B C - D C = 20 - \frac{80}{7} = \frac{60}{7} (c m) \end{array}$

b) $S_{A B C} = \frac{A H . B C}{2} = \frac{A B . A C}{2} \Rightarrow A H = \frac{A B . A C}{B C} = \frac{12.16}{20} = 9,6 (c m)$

Áp dụng định lý Pytago vào vuông tại H

$\Rightarrow B H = \sqrt{A B^{2} - A H^{2}} = \sqrt{12^{2} - {9,6}^{2}} = 7,2 (c m)$

$H D = |B D - B H| = |\frac{60}{7} - 7,2| = \frac{48}{35} (c m)$

$Δ A H D$ vuông tại H nên

$A D = \sqrt{A H^{2} + H D^{2}} (P y t a g o) = \sqrt{{9,6}^{2} + {(\frac{48}{35})}^{2}} = \frac{48 \sqrt{2}}{7} (c m)$

Vậy $A H = 9,6 c m; H D = \frac{48}{35} c m; A D = \frac{48 \sqrt{2}}{7} (c m)$

Câu 9:

Giải phương trình

$(x - \sqrt{2}) = 3 (x^{2} - 2)$

Xem đáp án

$\begin{array}{l} (x - \sqrt{2}) = 3 (x^{2} - 2) \Leftrightarrow (x - \sqrt{2}) [1 - 3 (x + \sqrt{2})] = 0 \\ \Leftrightarrow [\begin{array}{l} x = \sqrt{2} \\ x = \frac{1 + \sqrt{2}}{3} \end{array} S = \{\sqrt{2}; \frac{1 + \sqrt{2}}{3}\} \end{array}$

Câu 10:

Giải phương trình

$\frac{3 x}{2} - 2 x - 1 = \frac{x}{3}$

Xem đáp án

$\begin{array}{l} \frac{3 x}{2} - 2 x - 1 = \frac{x}{3} \Leftrightarrow (\frac{3}{2} - 2 - \frac{1}{3}) x = 1 \Leftrightarrow x = \frac{- 6}{5} S = \{\frac{- 6}{5}\} \end{array}$

Câu 11:

Giải phương trình (x+1)²=1

Xem đáp án

$\begin{array}{l} {(x + 1)}^{2} = 1 \Leftrightarrow {(x + 1)}^{2} - 1^{2} = 0 \Leftrightarrow (x + 1 - 1) (x + 1 + 1) = 0 \\ \Leftrightarrow x (x + 2) = 0 \Leftrightarrow [\begin{array}{l} x = 0 \\ x = - 2 \end{array} \end{array}$

Câu 12:

Giải phương trình

$\frac{2}{x - 2} = \frac{2}{3 x - 2}$

Xem đáp án

$\frac{2}{x - 2} = \frac{2}{3 x - 2} (\begin{array}{l} x \neq 2 \\ x \neq \frac{2}{3} \end{array}) \Rightarrow x - 2 = 3 x - 2 \Leftrightarrow x = 0 (t m) .$

Câu 13:

Giải phườn trình

$\frac{x}{x + 1} - \frac{6}{x - 1} = \frac{x^{2} - 8}{x^{2} - 1}$

Xem đáp án

$\begin{array}{l} \frac{x}{x + 1} - \frac{6}{x - 1} = \frac{x^{2} - 8}{x^{2} - 1} (x \neq \pm 1) \Leftrightarrow \frac{x (x - 1) - 6 (x + 1)}{(x - 1) (x + 1)} = \frac{x^{2} - 8}{x^{2} - 1} \\ \Rightarrow x^{2} - x - 6 x - 6 = x^{2} - 8 \Leftrightarrow 7 x = 2 \Leftrightarrow x = \frac{2}{7} (t m) \end{array}$

Câu 14:

Giải phương trình

$\frac{x - 3}{2011} + \frac{x - 2}{2012} - \frac{x - 2011}{3} = \frac{x - 2012}{2}$

Xem đáp án

$\begin{array}{l} \frac{x - 3}{2011} + \frac{x - 2}{2012} - \frac{x - 2011}{3} = \frac{x - 2012}{2} \\ \Leftrightarrow (\frac{x - 3}{2011} - 1) + (\frac{x - 2}{2012} - 1) - (\frac{x - 2011}{3} - 1) - (\frac{x - 2012}{2} - 1) = 0 \\ \Leftrightarrow \frac{x - 2014}{2011} + \frac{x - 2014}{2012} - \frac{x - 2014}{3} - \frac{x - 2014}{2} = 0 \\ \Leftrightarrow (x - 2014) (\frac{1}{2011} + \frac{1}{2012} - \frac{1}{3} - \frac{1}{2}) = 0 \Leftrightarrow x = 2014 \end{array}$

Câu 15:

Giải phương trình

$\frac{x - 1}{x + 2} - \frac{x}{x - 2} = \frac{- 13}{5}$

Xem đáp án

$\begin{array}{l} \frac{x - 1}{x + 2} - \frac{x}{x - 2} = - \frac{13}{5} (x \neq \pm 2) \\ \Leftrightarrow \frac{(x - 1) (x - 2) - x (x + 2)}{(x + 2) (x - 2)} = \frac{- 13 (x + 2) (x - 2)}{5 (x + 2) (x - 2)} \\ \Rightarrow 5 (x^{2} - 3 x + 2) - 5 (x^{2} + 2 x) = - 13 \\ \Leftrightarrow - 25 x = - 23 \Leftrightarrow x = \frac{23}{25} (t m) \end{array}$

Câu 16:

Giải phương trình

$\frac{2 x + 1}{2 x - 1} - \frac{2 x - 1}{2 x + 1} = \frac{8}{4 x^{2} - 1}$

Xem đáp án

$\begin{array}{l} \frac{2 x + 1}{2 x - 1} - \frac{2 x - 1}{2 x + 1} = \frac{8}{4 x^{2} - 1} (x \neq \pm \frac{1}{2}) \\ \Leftrightarrow \frac{{(2 x + 1)}^{2} - {(2 x - 1)}^{2}}{(2 x - 1) (2 x + 1)} = \frac{8}{(2 x - 1) (2 x + 1)} \\ \Rightarrow (2 x + 1 + 2 x - 1) (2 x + 1 - 2 x + 1) = 8 \\ \Leftrightarrow 4 x .2 = 8 \Leftrightarrow x = 1 (t m) S = \{1\} \end{array}$

Câu 17:

Giải phương trình

$\frac{3}{2 x - 16} + \frac{3 x - 20}{x - 8} + \frac{1}{8} = \frac{13 x - 102}{3 x - 24}$

Xem đáp án

$\begin{array}{l} \frac{3}{2 x - 16} + \frac{3 x - 20}{x - 8} + \frac{1}{8} = \frac{13 x - 102}{3 x - 24} (x \neq 8) \\ \Leftrightarrow \frac{3}{2 (x - 8)} + \frac{3 x - 20}{x - 8} + \frac{1}{8} = \frac{13 x - 102}{3 (x - 8)} \\ \Leftrightarrow \frac{12 + 8 (3 x - 20) + x - 8}{8 (x - 8)} = \frac{13 x - 102}{3 (x - 8)} \Leftrightarrow \frac{25 x - 156}{8 (x - 8)} = \frac{13 x - 102}{3 (x - 8)} \\ \Rightarrow 75 x - 468 = 104 x - 816 \Leftrightarrow x = 12 (t m) \end{array}$

Câu 18:

Giải phương trình

$\frac{x + 5}{x^{2} - 5 x} - \frac{x - 5}{2 x^{2} + 10 x} = \frac{x + 25}{2 x^{2} - 50}$

Xem đáp án

$\begin{array}{l} \frac{x + 5}{x^{2} - 5 x} - \frac{x - 5}{2 x^{2} + 10 x} = \frac{x + 25}{2 x^{2} - 50} (\begin{array}{l} x \neq 0 \\ x \neq \pm 5 \end{array}) \\ \Leftrightarrow \frac{x + 5}{x (x - 5)} - \frac{x - 5}{2 x (x + 5)} = \frac{x + 25}{2 (x - 5) (x + 5)} \\ \Leftrightarrow 2 (x + 5) (x + 5) - {(x - 5)}^{2} = x (x + 25) \\ \Leftrightarrow 2 x^{2} + 20 x + 50 - x^{2} + 10 x - 25 = x^{2} + 25 x \\ \Leftrightarrow 5 x = - 25 \Leftrightarrow x = - 5 (t m) \end{array}$

Câu 19:

Giải phương trình

$\frac{1}{x - 1} + \frac{2 x^{2} - 5}{x^{3} - 1} = \frac{4}{x^{2} + x + 1}$

Xem đáp án

$\begin{array}{l} \frac{1}{x - 1} + \frac{2 x^{2} - 5}{x^{3} - 1} = \frac{4}{x^{2} + x + 1} (x \neq 1) \\ \Leftrightarrow \frac{x^{2} + x + 1 + 2 x^{2} - 5}{(x - 1) (x^{2} + x + 1)} = \frac{4 (x - 1)}{(x - 1) (x^{2} + x + 1)} \\ \Rightarrow 3 x^{2} + x - 4 = 4 x - 4 \Leftrightarrow 3 x^{2} - 3 x = 0 \Leftrightarrow [\begin{array}{l} x = 0 (t m) \\ x = 1 (t m) \end{array} \end{array}$

Câu 20:

Giải phương trình

$\frac{x - 1}{x} + \frac{1}{x + 1} = \frac{2 x^{2} - 1}{x^{2} + x}$

Xem đáp án

$\begin{array}{l} \frac{x - 1}{x} + \frac{1}{x + 1} = \frac{2 x^{2} - 1}{x^{2} + x} (\begin{array}{l} x \neq 0 \\ x \neq - 1 \end{array}) \\ \Leftrightarrow \frac{(x - 1) (x + 1) + x}{x (x + 1)} = \frac{2 x^{2} - 1}{x (x + 1)} \\ \Rightarrow x^{2} - 1 + x = 2 x^{2} - 1 \Leftrightarrow x^{2} - x = 0 \\ \Leftrightarrow x (x - 1) = 0 \Leftrightarrow [\begin{array}{l} x = 0 (k t m) \\ x = 1 (t m) \end{array} \end{array}$

Câu 21:

Giải phương trình

$\frac{x}{x - 2} - \frac{5}{x + 2} = \frac{x^{2} + 1}{x^{2} - 4}$

Xem đáp án

$\begin{array}{l} \frac{x}{x - 2} - \frac{5}{x + 2} = \frac{x^{2} + 1}{x^{2} - 4} (\begin{array}{l} x \neq 2 \\ x \neq - 2 \end{array}) \\ \Leftrightarrow \frac{x (x + 2) - 5 (x - 2)}{(x - 2) (x + 2)} = \frac{x^{2} + 1}{(x - 2) (x + 2)} \\ \Rightarrow x^{2} + 2 x - 5 x + 10 = x^{2} + 1 \Leftrightarrow 3 x = 9 \Leftrightarrow x = 3 (t m) \end{array}$

Câu 22:

Giải phương trình

$\frac{3}{4 (x - 5)} + \frac{15}{50 - 2 x^{2}} = - \frac{7}{6 (x + 5)}$

Xem đáp án

$\begin{array}{l} \frac{3}{4 (x - 5)} + \frac{15}{50 - 2 x^{2}} = \frac{- 7}{6 (x + 5)} \\ \Leftrightarrow \frac{3}{4 (x - 5)} - \frac{15}{2 (x - 5) (x + 5)} = \frac{- 7}{6 (x + 5)} (x \neq \pm 5) \\ \Leftrightarrow \frac{3 (x + 5) - 15.2}{4 (x - 5) (x + 5)} = \frac{- 7}{6 (x + 5)} \\ \Rightarrow (3 x - 15) .6 (x + 5) = - 7.4 (x - 5) (x + 5) \\ \Leftrightarrow 3 (x - 5) .6 = - 28 (x - 5) \Leftrightarrow 18 = - 28 (V N) \\ S = \emptyset \end{array}$

Câu 23:

Giải phương trình

$\frac{8 x^{2}}{3 (1 - 4 x^{2})} = \frac{2 x}{6 x - 3} - \frac{1 + 8 x}{4 + 8 x}$

Xem đáp án

$\begin{array}{l} \frac{8 x^{2}}{3 (1 - 4 x^{2})} = \frac{2 x}{6 x - 3} - \frac{1 + 8 x}{4 + 8 x} (x \neq \pm \frac{1}{2}) \\ \Leftrightarrow \frac{8 x^{2}}{3 (1 - 2 x) (1 + 2 x)} = \frac{- 2 x}{3 (1 - 2 x)} - \frac{1 + 8 x}{4 (1 + 2 x)} \\ \Leftrightarrow \frac{4.8 x^{2}}{12 (1 - 2 x) (1 + 2 x)} = \frac{4. (- 2 x) . (1 + 2 x) - 3. (1 + 8 x) . (1 - 2 x)}{12. (1 - 2 x) (1 + 2 x)} \\ \Rightarrow 32 x^{2} = - 8 x - 16 x^{2} - 3 + 18 x + 48 x^{2} \\ \Leftrightarrow 10 x = 3 \Leftrightarrow x = \frac{3}{10} (t m) \end{array}$

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bài tập cuối tuần Học kì 2 Toán 8 có đáp án

Bài tập theo tuần Toán 8 - Tuần 23

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương