15 câu hỏi trắc nghiệm thuộc Bài tập theo tuần Toán 8 - Tuần 33

Câu 1:

Phương trình nào sau đây là phương trình bậc nhất một ẩn

$A . 5 x + 5 y = 0$

$B . \frac{2}{x} - 5 = 0$

$C . - \frac{1}{2} x + 1 = 0$

$D . 0 x + 3 = 0$

Xem đáp án

Đáp án C

Câu 2:

Điều kiện xác định của phương trình

\frac{x + 3}{x (x - 2)} = 0

là

$A . x \neq 0; x \neq - 3$

$B . x \neq 0; x \neq 2$

$C . x \neq 0; x \neq 3$

$D . x = 0; x = 2$

Xem đáp án

Đáp án B

Câu 3:

Tập nghiệm của phương trình (x+1)(x-2)=0 là:

$A . \{- 1; 2\}$

$B . \{- 1; - 2\}$

$C . \{1; 2\}$

$D . \{- 1; - 2\}$

Xem đáp án

Đáp án A

Câu 4:

Hình vẽ sau biểu diễn tập nghiệm của bất phương trình nào

$A . x \leq 3$

$B . x \leq - 3$

$C . x \geq 3$

$D . x \geq - 3$

Xem đáp án

Đáp án C

Câu 5:

Tam giác ABC có AD là đường phân giác thì

$A . \frac{A B}{A C} = \frac{D B}{D C}$

$B . \frac{B D}{D C} = \frac{A C}{A B}$

$C . \frac{A B}{A C} = \frac{D C}{D B}$

$D . \frac{D C}{A C} = \frac{A B}{B D}$

Xem đáp án

Đáp án A

Câu 6:

Cho tam giác ABC đồng dạng với tam giác A'B'C' theo tỉ số 2/3 . Vậy tỉ số diện tích của tam giác A'B'C' và tam giác ABC là

$A . \frac{S_{A' B' C'}}{S_{A B C}} = \frac{3}{2}$

$B . \frac{S_{A' B' C}}{S_{A B C}} = \frac{2}{3}$

$C . \frac{S_{A' B' C}}{S_{A B C}} = \frac{4}{9}$

$D . \frac{S_{A' B' C}}{S_{A B C}} = \frac{9}{4}$

Xem đáp án

Đáp án D

Câu 7:

Diện tích một mặt của hình lập phương là $64 c m^{2} .$ Thì thể tích của nó là

$A . 512 c m^{3}$

$B . 256 c m^{3}$

$C . 196 c m^{3}$

$D . 128 c m^{3}$

Xem đáp án

Đáp án A

Câu 8:

Thể tích của một hình hộp chữ nhật có các kích thước là 2cm; 4 cm; 5 cm bằng

$A . 80 c m^{3}$

$B . 40 c m^{3}$

$C . 120 c m^{3}$

$D . 160 c m^{3}$

Xem đáp án

Đáp án B

Câu 9:

Giải các phương trình và bất phương trình sau

2x+11=2-x

Xem đáp án

$\begin{array}{l} 2 x + 11 = 2 - x \Leftrightarrow 3 x = 2 - 11 \\ \Leftrightarrow 3 x = - 9 \Leftrightarrow x = - 3 \end{array}$

Vậy $S = \{- 3\}$

Câu 10:

Giải phương trình

\frac{2 x}{x + 1} + \frac{5}{x - 1} = \frac{2 x^{2} - 1}{x^{2} - 1}

Xem đáp án

$\begin{array}{l} \frac{2 x}{x + 1} + \frac{5}{x - 1} = \frac{2 x^{2} - 1}{x^{2} - 1} (\begin{array}{l} x \neq 1 \\ x \neq - 1 \end{array}) \\ \Leftrightarrow \frac{2 x (x - 1) + 5 (x + 1)}{(x - 1) (x + 1)} = \frac{2 x^{2} - 1}{x^{2} - 1} \\ \Rightarrow 2 x^{2} - 2 x + 5 x + 5 = 2 x^{2} - 1 \\ \Leftrightarrow 3 x = - 6 \Leftrightarrow x = - 2 (t / m) \end{array}$

Câu 11:

$x (x - 6) > x^{2} + x - 14$

Xem đáp án

$\begin{array}{l} x (x - 6) > x^{2} + x - 14 \\ \Leftrightarrow x^{2} - 6 x > x^{2} + x - 14 \\ \Leftrightarrow - 6 x - x > - 14 \\ \Leftrightarrow - 7 x > - 14 \\ \Leftrightarrow x < 2 \end{array}$

Vậy

S = \{x / x < 2\}

Câu 12:

Một người đi xe máy từ A đến B với vận tốc trung bình 40 km/h. Lúc về người ấy đi với vận tốc trung bình 30 km/h, biết rằng thời gian cả đi lẫn về hết 3 giờ 30 phút. Tính quãng đường AB.

Xem đáp án

Gọi x (km) là quãng đường AB

Thời gian lúc đi là : $\frac{x}{40}$ ;Thời gian lúc về: $\frac{x}{30}$

Thời gian cả đi lẫn về : $3 h 30' = \frac{7}{2} h$

Theo bài ta có phương trình: $\frac{x}{40} + \frac{x}{30} = \frac{7}{2} \Leftrightarrow \frac{3 x + 4 x}{120} = \frac{7}{2} \Leftrightarrow 14 x = 840 \Leftrightarrow x = 60 (t / m)$

Vậy quãng dường AB dài 60 km

Câu 13:

Cho tam giác ABC vuông tại A có AB = 3 cm, AC = 4 cm. từ B kẻ tia Bx song song với AC (Tia Bx thuộc nửa mặt phẳng bờ AB chứa điểm C), tia phân giác của góc BAC cắt BC tại M và cắt Bx tại N.

a) Chứng minh tam giác BMN đồng dạng với tam giác CMA

b) Chứng minh $\frac{A B}{A C} = \frac{M N}{A M}$

c) Tính BM, MC. Tính tỉ số diện tích tam giác ABM và tam giác AMC

Xem đáp án

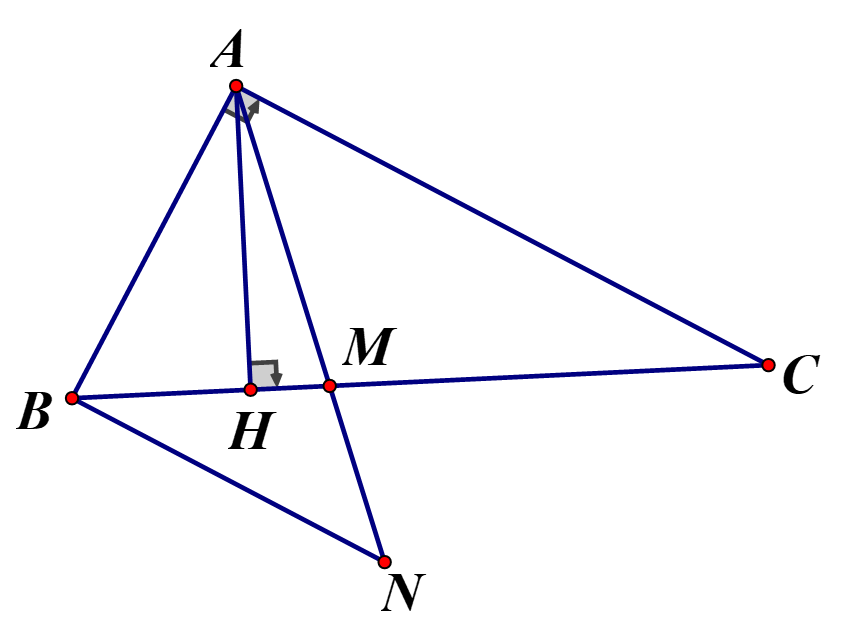
Cho tam giác ABC vuông tại A có AB = 3 cm, AC = 4 cm. từ B kẻ tia Bx song song với AC (Tia Bx thuộc nửa mặt phẳng bờ AB chứa điểm C), (ảnh 1)

a) Xét $Δ B M N$ và $Δ A M C$ có : $\hat{B M N} = \hat{A M C}$ (đối đỉnh) ; $\hat{C A N} = \hat{A N B}$ (so le trong)

b) $\Rightarrow Δ B M N ~ Δ C M A (g - g)$

$Δ B M N ~ Δ C M A \Rightarrow \frac{M B}{C M} = \frac{M N}{M A} (1)$

$Δ A M C$ có AM là đường phân giác $\Rightarrow \frac{A B}{A C} = \frac{B M}{C M} (2)$

Từ (1) và (2) ta có: $\frac{A B}{A C} = \frac{M N}{A M}$

c) Áp dụng định lý Pytago vào $Δ A B C \Rightarrow B C = \sqrt{A B^{2} + A C^{2}} = \sqrt{3^{2} + 4^{2}} = 5 (c m)$

Ta có $\frac{A B}{A C} = \frac{B M}{C M}$ (từ (2)) $\Rightarrow \frac{A B}{A B + A C} = \frac{B M}{B M + M C}$ hay $\frac{3}{3 + 4} = \frac{B M}{5} \Rightarrow B M = \frac{15}{7} (c m)$

$\Rightarrow M C = 5 - \frac{15}{7} = \frac{20}{7} (c m) \Rightarrow \frac{S_{A B M}}{S_{A M C}} = \frac{\frac{1}{2} A H . B M}{\frac{1}{2} A H . M C} = \frac{B M}{M C} = \frac{15 / 7}{20 / 7} = \frac{3}{4}$

Câu 14:

Cho tam giác ABC vuông tại A có AB = 3 cm, AC = 4 cm. từ B kẻ tia Bx song song với AC (Tia Bx thuộc nửa mặt phẳng bờ AB chứa điểm C), tia phân giác của góc BAC cắt BC tại M và cắt Bx tại N.

a) Chứng minh tam giác BMN đồng dạng với tam giác CMA

b) Chứng minh $\frac{A B}{A C} = \frac{M N}{A M}$

c) Tính BM, MC. Tính tỉ số diện tích tam giác ABM và tam giác AMC

Xem đáp án

a) Xét $Δ B M N$ và $Δ A M C$ có : $\hat{B M N} = \hat{A M C}$ (đối đỉnh) ; $\hat{C A N} = \hat{A N B}$ (so le trong)

b) $\Rightarrow Δ B M N ~ Δ C M A (g - g)$

$Δ B M N ~ Δ C M A \Rightarrow \frac{M B}{C M} = \frac{M N}{M A} (1)$

$Δ A M C$ có AM là đường phân giác $\Rightarrow \frac{A B}{A C} = \frac{B M}{C M} (2)$

Từ (1) và (2) ta có: $\frac{A B}{A C} = \frac{M N}{A M}$

c) Áp dụng định lý Pytago vào $Δ A B C \Rightarrow B C = \sqrt{A B^{2} + A C^{2}} = \sqrt{3^{2} + 4^{2}} = 5 (c m)$

Ta có $\frac{A B}{A C} = \frac{B M}{C M}$ (từ (2)) $\Rightarrow \frac{A B}{A B + A C} = \frac{B M}{B M + M C}$ hay $\frac{3}{3 + 4} = \frac{B M}{5} \Rightarrow B M = \frac{15}{7} (c m)$

$\Rightarrow M C = 5 - \frac{15}{7} = \frac{20}{7} (c m) \Rightarrow \frac{S_{A B M}}{S_{A M C}} = \frac{\frac{1}{2} A H . B M}{\frac{1}{2} A H . M C} = \frac{B M}{M C} = \frac{15 / 7}{20 / 7} = \frac{3}{4}$

Câu 15:

Tìm giá trị của phân thức

A = \frac{x - y}{x + y}

trong đó

x > y > 0

và biết rằng

x^{2} + y^{2} = 3 \frac{1}{3} x y

Xem đáp án

$A = \frac{x - y}{x + y} (d o x > y > 0 \Rightarrow A > 0)$

$\Rightarrow A^{2} = \frac{{(x - y)}^{2}}{{(x + y)}^{2}} = \frac{x^{2} + y^{2} - 2 x y}{x^{2} + y^{2} + 2 x y} = \frac{\frac{10}{3} x y - 2 x y}{\frac{10}{3} x y + 2 x y} = \frac{\frac{4}{3} x y}{\frac{16}{3} x y} = \frac{1}{4}$

mà A > 0 nên $A = \frac{1}{2}$

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bài tập cuối tuần Học kì 2 Toán 8 có đáp án

Bài tập theo tuần Toán 8 - Tuần 33

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương