Đề thi Giữa kì 1 Toán 8 có đáp án (Đề 6)
-
4329 lượt thi
-
5 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
a) 5x3y : xy – 2x2+ 10;
b) 2x(3x + 2) + (4x + 3)(2x – 1);
c) (x + 2)2– (x + 5)(x – 5);
d) (4x + 5)2– (8x + 10)(1 – 3x) + (1 – 3x)2.
 Xem đáp án
Xem đáp án
Hướng dẫn giải
a) 5x3y : xy – 2x2+ 10
= 5x2– 2x2+ 10
= 3x2+ 10
b) 2x(3x + 2) + (4x + 3)(2x – 1)
= 6x2+ 4x + 8x2– 4x + 6x – 3
= 14x2+ 6x – 3
c) (x + 2)2– (x + 5)(x – 5)
= x2+ 4x + 4 – x2+ 25
= 4x + 29
d) (4x + 5)2– (8x + 10)(1 – 3x) + (1 – 3x)2
= (4x + 5)2 – 2(4x + 5)(1 – 3x) + (1 – 3x)2
= [(4x + 5) – (1 – 3x)]2
= (4x + 5 – 1+ 3x)2
= (7x + 4)2
= 49x2+ 56x + 16
Câu 2:
a) 8x2+ 16xy
b) 3(x + 12) – x2– 12x
c) x2– 6x – z2+ 9
d) x2– 2x – 15
 Xem đáp án
Xem đáp án
Hướng dẫn giải
a) 8x2+ 16xy
= 8x(x + 2y)
b) 3(x + 12) – x2– 12x
= 3(x + 12) – x(x + 12)
= (x + 12)(3 – x)
c) x2– 6x – z2+ 9
= (x2– 6x + 9) – z2
= (x – 3)2– z2
= (x – 3 + z)(x – 3 – z)
d) x2– 2x – 15
= x2– 5x + 3x – 15
= x(x – 5) + 3(x – 5)
= (x – 5)(x + 3)
Câu 3:
a) x(x + 4) – x2= 10
b) 5x2+ 2x = 0
c) x2– 16 = x + 4
d) (4x – 1)2– (x + 7)2= 0
 Xem đáp án
Xem đáp án
Hướng dẫn giải
a) x(x + 4) – x2= 10
x2+ 4x – x2= 10
4x = 10
\(x = \frac{5}{2}\)
Vậy \(x = \frac{5}{2}\)
b) 5x2+ 2x = 0
x(5x + 2) = 0
\( \Rightarrow \left[ \begin{array}{l}x = 0\\5x + 2 = 0\end{array} \right.\)
\( \Rightarrow \left[ \begin{array}{l}x = 0\\x = \frac{{ - 2}}{5}\end{array} \right.\)
Vậy x = 0 và \(x = \frac{{ - 2}}{5}\).
c) x2– 16 = x + 4
(x + 4)(x – 4) – (x + 4) = 0
(x + 4)(x – 4 – 1) = 0
(x + 4)(x – 5) = 0
\( \Rightarrow \left[ \begin{array}{l}x + 4 = 0\\x - 5 = 0\end{array} \right.\)
\( \Rightarrow \left[ \begin{array}{l}x = - 4\\x = 5\end{array} \right.\)
Vậy x = 4 và x = 5.
d) (4x – 1)2– (x + 7)2= 0
(4x – 1 – x – 7)(4x – 1 + x + 7) =0
(3x – 8)(5x + 6) = 0
\( \Rightarrow \left[ \begin{array}{l}3x - 8 = 0\\5x + 6 = 0\end{array} \right.\)
\( \Rightarrow \left[ \begin{array}{l}x = \frac{8}{3}\\x = \frac{{ - 6}}{5}\end{array} \right.\)
Vậy \(x = \frac{8}{3}\) và \(x = \frac{{ - 6}}{5}\).
Câu 4:
a) Chứng minh tứ giác HCQB là hình bình hành.
b) Chứng minh CQ ⊥ AC và BQ ⊥ AB.
c) Trên tia HD lấy P sao cho HD = DP. CHứng minh DM là đường trung bình của tam giác PHQ từ đó chứng minh tứ giác BPQC là hình thang cân.
d) Gọi giao điểm của đoạn thẳng HP và đoạn thẳng BQ là G. Tam giác ABC cần bổ sung điều kiện gì để tứ giác HCQG là hình thang cân.
 Xem đáp án
Xem đáp án
Hướng dẫn giải
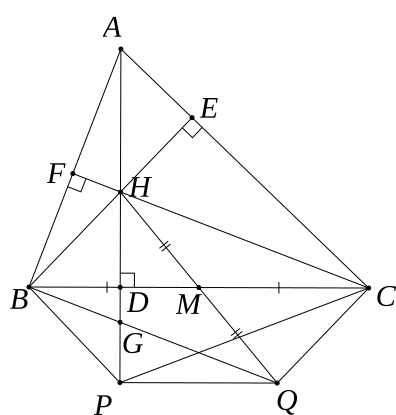
a) Tứ giác HCQB có:
M là trung điểm của BC (gt)
M là trung điểm của HQ (HM = MQ)
⇒ Tứ giác HCQB là hình bình hành. (tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường).
b) Vì HCQB là hình bình hành
⇒ BH//CQ hay BE//CQ
Mà BE ⊥ AC (BE là đường cao của ΔABC)
⇒ CQ ⊥ AC (đpcm)
Trong tam giác ABC có BE ⊥ AC, AD ⊥ BC và H là giao điểm của BE, AD
⇒ CH là đường cao thứ 3 của ΔABC
⇒ CH ⊥ AB. Gọi CH cắt AB tại F.
Vì HCQB là hình bình hành
⇒ FC//BQ
Mà FC ⊥ AB (cmt)
⇒ BQ ⊥ AB (đpcm)
c) Tam giác PHQ có:
M là trung điểm của HQ
D là trung điểm của HP
⇒ DM là đường trung bình tam giác PHQ
⇒ DM // PQ hay BC // PQ
⇒ BPQC là hình thang
Xét tam giác PHC có
HP ⊥ BC (vì AH ⊥ BC)
HD = DP (gt)
⇒ Tam giác PHC là tam giác cân
⇒ HC = PC
Mà HC = BQ (tính chất hình bình hành)
⇒ BQ = PC
Xét hình thang BPQC có BQ = PC (cmt)
⇒ BPQC là hình thang cân.
d) Giả sử HCQG là hình thang cân
\( \Rightarrow \widehat {HCQ} = \widehat {GHC}\)
Mà \(\widehat {HCQ} + \widehat {HCA} = 90^\circ \) và \(\widehat {GHC} + \widehat {HCB} = 90^\circ \)
\( \Rightarrow \widehat {HCA} = \widehat {HCB}\)
⇒ CF là đường phân giác của tam giác ABC
Mà CF là đường cao của tam giác ABC
⇒ Tam giác ABC cân tại C.
Vậy tam giác ABC cân tại C thì HCQG là hình thang cân.
Câu 5:
Chứng minh rằng trong 3 số x, y, z có ít nhất hai số bằng nhau hoặc đối nhau.
 Xem đáp án
Xem đáp án
Hướng dẫn giải
x2y – y2x + x2z – z2x + y2z + z2y = 2xyz
⇔ x2y + x2z – y2x – xyz – xyz – z2x + y2z + z2y = 0
⇔ x(xy + xz – y2 – yz) – z(xy + zx – y2 – zy) = 0
⇔ (xy + xz – y2 – yz)(x – z) = 0
⇔ [x(y + z) – y(y + z)](x – z) = 0
⇔ (y + z)(x – y)(x – z) = 0
\( \Leftrightarrow \left[ \begin{array}{l}y = - z\\x = y\\x = z\end{array} \right.\)
⇒ 3 số x, y, z có ít nhất hai số bằng nhau hoặc đối nhau. (đpcm)
