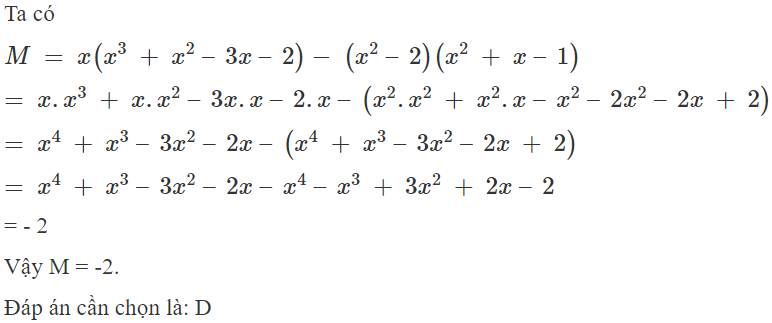Trắc nghiệm Nhân đơn thức với đa thức (có đáp án)
-
1762 lượt thi
-
27 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 3:
Biết 3x + 2(5 - x) = 0, giá trị của x cần tìm là
 Xem đáp án
Xem đáp án
Ta có:
3x + 2(5 - x) = 0
3x + 2.5 - 2.x = 0
x + 10 = 0
x = - 10
Chọn đáp án A.
Câu 11:
Cho hình thang có đáy lớn gấp đôi đáy nhỏ, đáy nhỏ lớn hơn chiều cao 2 đơn vị. Biểu thức tính diện tích hình thang là
 Xem đáp án
Xem đáp án
Gọi x (x > 2) là độ dài đáy nhỏ của hình thang
Theo giả thiết ta có độ dài đáy lớn là 2x, chiều cao của hình thang là x – 2
Diện tích hình thang là
S = (đvdt)
Đáp án cần chọn: B
Câu 12:
Cho hình chữ nhật có chiều dài lớn hơn chiều rộng là 5 đơn vị. Biểu thức tính diện tích hình chữ nhật là:
 Xem đáp án
Xem đáp án
Gọi x ( x > 0) là chiều rộng của hình chữ nhật
Theo giả thiết ta có chiều dài hình chữ nhật là x + 5
Diện tích hình chữ nhật là S = x(x + 5) = x2 + 5x (đvdt)
Đáp án cần chọn là: A
Câu 14:
Giá trị của biểu thức P = (3x – 1)(2x + 3) – (x – 5)(6x – 1) – 38x là
 Xem đáp án
Xem đáp án
a có
P = (3x – 1)(2x + 3) – (x – 5)(6x – 1) – 38x
= 3x.2x + 3x.3 – 1.2x – 1.3 – (x.6x – x – 5.6x – 5.(-1)) – 38x
= 6x2 + 9x – 2x – 3 – 6x2 + x + 30x – 5 – 38x
= (6x2 – 6x2) + (9x – 2x + x + 30x – 38x) – 3 – 5
= -8
Vậy P = -8
Đáp án cần chọn là: A
Câu 15:
Cho
A = (3x + 7)(2x + 3) – (3x – 5)(2x + 11);
B = x(2x + 1) – (x + 2) + – x + 3.
Chọn khẳng định đúng
 Xem đáp án
Xem đáp án
A = (3x + 7)(2x + 3) – (3x – 5)(2x + 11)
= 3x.2x + 3x.3 + 7.2x + 7.3 – (3x.2x + 3x.11 – 5.2x – 5.11)
"<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>=</mo><mo> </mo><mn>6</mn><msup><mi>x</mi><mn>2</mn></msup><mo> </mo><mo>+</mo><mo> </mo><mn>9</mn><mi>x</mi><mo> </mo><mo>+</mo><mo> </mo><mn>14</mn><mi>x</mi><mo> </mo><mo>+</mo><mo> </mo><mn>21</mn><mo> </mo><mo>–</mo><mo> </mo><mo>(</mo><mn>6</mn><msup><mi>x</mi><mn>2</mn></msup><mo> </mo><mo>+</mo><mo> </mo><mn>33</mn><mi>x</mi><mo> </mo><mo>–</mo><mo> </mo><mn>10</mn><mi>x</mi><mo> </mo><mo>–</mo><mo> </mo><mn>55</mn><mo>)</mo><mo> </mo><mo> </mo><mspace linebreak="newline" /><mo>=</mo><mo> </mo><mn>6</mn><msup><mi>x</mi><mn>2</mn></msup><mo> </mo><mo>+</mo><mo> </mo><mn>23</mn><mi>x</mi><mo> </mo><mo>+</mo><mo> </mo><mn>21</mn><mo> </mo><mo>–</mo><mo> </mo><mn>6</mn><msup><mi>x</mi><mn>2</mn></msup><mo> </mo><mo>–</mo><mo> </mo><mn>33</mn><mi>x</mi><mo> </mo><mo>+</mo><mo> </mo><mn>10</mn><mi>x</mi><mo> </mo><mo>+</mo><mo> </mo><mn>55</mn><mo> </mo><mo>=</mo><mo> </mo><mn>76</mn></math>"> "<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>B</mi><mo> </mo><mo>=</mo><mo> </mo><mi>x</mi><mo>(</mo><mn>2</mn><mi>x</mi><mo> </mo><mo>+</mo><mo> </mo><mn>1</mn><mo>)</mo><mo> </mo><mo>–</mo><mo> </mo><msup><mi>x</mi><mn>2</mn></msup><mo>(</mo><mi>x</mi><mo> </mo><mo>+</mo><mo> </mo><mn>2</mn><mo>)</mo><mo> </mo><mo>+</mo><mo> </mo><msup><mi>x</mi><mn>3</mn></msup><mo> </mo><mo>–</mo><mo> </mo><mi>x</mi><mo> </mo><mo>+</mo><mo> </mo><mn>3</mn><mo> </mo><mo> </mo><mspace linebreak="newline" /><mo>=</mo><mo> </mo><mi>x</mi><mo>.</mo><mn>2</mn><mi>x</mi><mo> </mo><mo>+</mo><mo> </mo><mi>x</mi><mo> </mo><mo>–</mo><mo> </mo><mo>(</mo><msup><mi>x</mi><mn>2</mn></msup><mo>.</mo><mi>x</mi><mo> </mo><mo>+</mo><mo> </mo><mn>2</mn><msup><mi>x</mi><mn>2</mn></msup><mo>)</mo><mo> </mo><mo>+</mo><mo> </mo><msup><mi>x</mi><mn>3</mn></msup><mo> </mo><mo>–</mo><mo> </mo><mi>x</mi><mo> </mo><mo>+</mo><mo> </mo><mn>3</mn><mo> </mo><mo> </mo><mspace linebreak="newline" /><mo>=</mo><mo> </mo><mn>2</mn><msup><mi>x</mi><mn>2</mn></msup><mo> </mo><mo>+</mo><mo> </mo><mi>x</mi><mo> </mo><mo>–</mo><mo> </mo><msup><mi>x</mi><mn>3</mn></msup><mo> </mo><mo>–</mo><mo> </mo><mn>2</mn><msup><mi>x</mi><mn>2</mn></msup><mo> </mo><mo>+</mo><mo> </mo><msup><mi>x</mi><mn>3</mn></msup><mo> </mo><mo>–</mo><mo> </mo><mi>x</mi><mo> </mo><mo>+</mo><mo> </mo><mn>3</mn><mo> </mo><mo>=</mo><mo> </mo><mn>3</mn></math>">B = x(2x + 1) – x2(x + 2) + x3 – x + 3 = x.2x + x – (x2.x + 2x2) + x3 – x + 3 = 2x2 + x – x3 – 2x2 + x3 – x + 3 = 3Từ đó ta có A = 76; B = 3 mà 76 = 25.3 + 1 nên A = 25B + 1
Đáp án cần chọn là: C
Câu 16:
Cho M = -3(x – 4)(x – 2) + x(3x – 18) – 25; N = (x – 3)(x + 7) – (2x – 1)(x + 2) + x(x – 1). Chọn khẳng định đúng.
 Xem đáp án
Xem đáp án
M = -3(x – 4)(x – 2) + x(3x – 18) – 25
= -3(– 2x – 4x + 8) + x.3x + x.(-18) – 25
= -3 + 6x + 12x – 24 + 3x2 – 18x – 25
= (-3 + 3) + (6x + 12x – 18x) – 24 – 25
= -49
N = (x – 3)(x + 7) – (2x – 1)(x + 2) + x(x – 1)
= x.x + x.7 – 3.x – 3.7 – (2x.x + 2x.2 – x – 1.2) + x.x + x.(-1)
= + 7x – 3x – 21 – 2 – 4x + x + 2 + – x
= ( – 2 + x2) + (7x – 3x – 4x + x – x) – 21 + 2
= -19
Vậy M = -49; N = -19 => M – N = -30
Đáp án cần chọn là: B
Câu 17:
Gọi x là giá trị thỏa mãn 5(3x + 5) – 4(2x – 3) = 5x + 3(2x – 12) + 1. Khi đó
 Xem đáp án
Xem đáp án
Ta có
5(3x + 5) − 4(2x − 3) = 5x + 3(2x − 12) + 1
15x + 25 − 8x + 12 = 5x + 6x – 36 + 1
7x + 37 = 11x − 35
4x = 72
x = 18
Vậy x = 18.
Suy ra 17 < x < 19.
Đáp án cần chọn là: C
Câu 18:
Gọi x là giá trị thỏa mãn (3x – 4)(x – 2) = 3x(x – 9) – 3. Khi đó
 Xem đáp án
Xem đáp án
Ta có:
(3x – 4)(x – 2) = 3x(x – 9) – 3
3x.x+ 3x.(-2) – 4.x – 4.(-2) = 3x.x + 3x.(-9) – 3
3– 6x -4x + 8 = 3 – 27x – 3
17x = -11
x =
Vậy x =
Đáp án cần chọn là: A
Câu 19:
Tính giá trị của biểu thức
tại x = 12
 Xem đáp án
Xem đáp án
Ta có:
P=x10 − 13x9 + 13x8 − 13x7 + … − 13x + 10 = x10 − 12x9 − x9 + 12x8 + x8 − 12x7 − x7 + 12x6 + … +x2 − 12x − x + 10 = x9(x − 12) − x8(x − 12) + x7(x − 12) − … + x(x − 12) − x
Câu 20: Tính bằng cách hợp lý giá trị của A = tại x = 71. Ta có A = x5 – 70x4 – 70x3 – 70x2 – 70x + 29 = x5 – 71x4 + x4 – 71x3 + x3 – 71x2 + x2 – 71x + x – 71 + 100 = x4(x – 71) + x3(x – 71) + x2(x – 71) + x(x – 71) + (x – 71) + 100 Vì x = 71 nên x – 71 = 0, thay x – 71 = 0 vào A ta đươc A = = 100 Vậy A = 100 Đáp án cần chọn là: C
Câu 21:
Xác định hệ số a, b, c biết rằng với mọi giá trị của x thì
ax_Preview" style="box-sizing: border-box; color: inherit; font-style: normal; font-variant-ligatures: normal; font-variant-caps: normal; font-weight: 400; letter-spacing: normal; orphans: 2; text-align: start; text-indent: 0px; text-transform: none; white-space: normal; widows: 2; word-spacing: 0px; -webkit-text-stroke-width: 0px; background-color: #ffffff; text-decoration-thickness: initial; text-decoration-style: initial; text-decoration-color: initial;">
 Xem đáp án
Xem đáp án
Ta có:
Theo bài ra ta có:
đúng với mọi x
đúng với mọi x.
Vậy a = 9, b = 6, c = -4
Đáp án cần chọn là: B
Câu 22:
Cho , đẳng thức nào sau đây đúng?
 Xem đáp án
Xem đáp án
Ta có:
2(x + 1)(y + 1) = 2(xy + x + y + 1) = 2xy + 2x + 2y + 2
Thay ta được:
2xy + 2x + 2y + x2+ y2 = (x2+ xy + 2x) + (y2 + xy + 2y)= x(x + y + 2) + y(x + y + 2) = (x + y)(x + y +2)
Từ đó ta có: 2(x + 1)(y + 1) = (x + y)(x + y + 2)
Đáp án cần chọn là: B
Câu 23:
Cho biết (x + y)(x + z) + (y + z)(y + x) = 2(z + x)(z + y). Khi đó
 Xem đáp án
Xem đáp án
Ta có
(x + y)(x + z) + (y + z)(y + x) = 2(z + x)(z + y).
⇔x.x. + xz + yx + yz + y.y + yx + zy + zx = 2(z.z + zy + zx + xy)
⇔ x2 + 2xz + 2xy + 2yxz+ y2 = 2z2 + 2zy + 2xz + 2xy ⇔ x2 + 2xz + 2xy + 2yz + y2 – 2z2 – 2zy – 2xz – 2xy = 0 ⇔ x2 + y2 – 2z2 = 0 ⇔ x2 + y2 = 2z2 ⇔ z2 = (x2+y2)/2Đáp án cần chọn là: A
Câu 24:
Cho các số x, y, z tỉ lệ với các số a, b, c. Khi đó bằng
 Xem đáp án
Xem đáp án
Vì x, y, z tỉ lệ với các số a, b, c nên suy ra x = ka, y = kb, z = kc
Thay x = ka, y = kb, z = kc vào ta được
[(ka)2 + 2(kb)2 + 3(kc)2](a2 + 2b2 + 3c2) = (k2a2 + 2k2b2 + 3k2c2)(a2 + 2b2 + 3c2) = k2(a2 + 2b2 + 3c2)(a2 + 2b2 + 3c2)
Câu 25: Cho B = (m – 1)(m + 6) – (m + 1)(m – 6). Chọn kết luận đúng. Ta có B = (m – 1)(m + 6) – (m + 1)(m – 6) = m2 + 6m – m – 6 – (m2 – 6m + m – 6) = m2 + 5m – 6 – m2 + 6m – m + 6 = 10m Nhận thấy 10 ⁝ 10 => 10.m ⁝ 10 nên B ⁝ 10 với mọi giá trị nguyên của m. Đáp án cần chọn là: A
Câu 26:
Cho m số mà mỗi số bằng 3n – 1 và n số mà mỗi số bằng 9 – 3m. Biết tổng tất cả các số đó bằng 5 lần tổng m + n. Khi đó
 Xem đáp án
Xem đáp án
+ Tổng của m số mà mỗi số bằng 3n – 1 là m(3n – 1)
+ Tổng của n số mà mỗi số bằng 9 – 3m là n(9 – 3m)
Tổng tất cả các số trên là m(3n – 1) + n(9 – 3m)
Theo đề bài ta có
m(3n – 1) + n(9 – 3m) = 5(m + n)
<=> 3mn – m + 9n – 3mn = 5m + 5n
<=> 6m = 4n <=> m = 2/3 n
Vậy
Đáp án cần chọn là: A
Câu 27:
Tính tổng các hệ số của lũy thừa bậc ba, lũy thừa bậc hai và lũy thừa bậc nhất trong kết quả của phép nhân
(x2 + x + 1)(x3 – 2x + 1)
 Xem đáp án
Xem đáp án
Ta có
(x2 + x + 1)(x3 – 2x + 1) = x2.x3 + x2.(−2x) + x2.1 + x.x3 + x.(−2x) + x.1 + 1.x3 + 1.(−2x) + 1.1 = x5 – 2x3 + x2 + x4 – 2x2 + x + x3 – 2x + 1 = x5 + x4 – x3 – x2 – x +
Bắt đầu thi ngay