10 câu hỏi trắc nghiệm thuộc Trắc nghiêm Phương trình tích có đáp án (Vận dụng)

Câu 1:

Tập nghiệm của phương trình (x² + x)(x² + x + 1) = 6 là

A. S = {-1; -2}

B. S = {1; 2}

C. S = {1; -2}

D. S = {-1; 2}

Xem đáp án

Đáp án cần chọn là: C

Đặt x² + x = y, ta có

y(y + 1) = 6 $\Leftrightarrow$ y² + y – 6 = 02²

$\Leftrightarrow$ y² – 2y + 3y – 6 = 0

$\Leftrightarrow$ y(y – 2) + 3(y – 2) = 0

$\Leftrightarrow$ (y – 2)(y + 3) = 0

$\Leftrightarrow [\begin{array}{l} y = - 3 \\ y = 2 \end{array}$

+ Với y = –3, ta có x² + x + 3 = 0, vô nghiệm vì

x² + x + 3 = ${(x + \frac{1}{2})}^{2} + \frac{11}{4} > 0$

+ Với y = 2, ta có x² + x – 2 = 0 $\Leftrightarrow$ x² + 2x – x – 2 = 0

$\Leftrightarrow$ x(x + 2) – (x + 2) = 0

$\Leftrightarrow$ (x + 2)(x – 1) = 0

$\Leftrightarrow [\begin{array}{l} x + 2 = 0 \\ x - 1 = 0 \end{array} \Leftrightarrow [\begin{array}{l} x = - 2 \\ x = 1 \end{array}$

Vậy S = {1;-2}

Câu 2:

Tập nghiệm của phương trình (x² – x – 1)(x² – x + 1) = 3 là

A. S = {-1; -2}

B. S = {1; 2}

C. S = {1; -2}

D. S = {-1; 2}

Xem đáp án

Đáp án cần chọn là: D

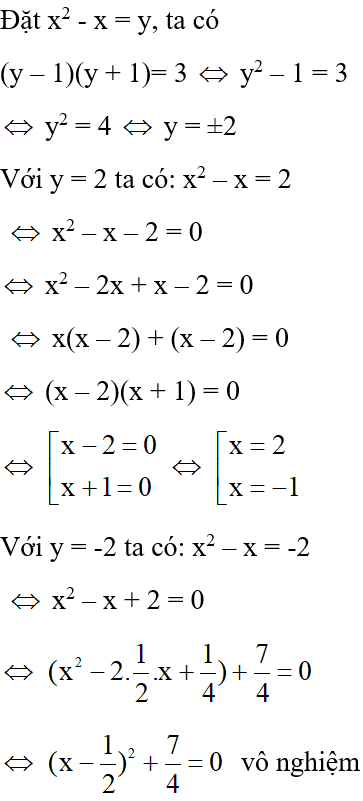
vì với mọi x R

Vậy tập nghiệm của phương trình là S = {-1; 2}

Câu 3:

Tìm m để phương trình (2m – 5)x – 2m²+ 8 = 43 có nghiệm x = -7

A. m = 0 hoặc m = 7

B. m = 1 hoặc m = -7

C. m = 0 hoặc m = -7

D. m = -7

Xem đáp án

Đáp án cần chọn là: C

Thay x = -7 vào phương trình (2m – 5)x – 2m²+ 8 = 43 ta được:

(2m – 5)(-7) – 2m² + 8 = 43

$\Leftrightarrow$ -14m + 35 – 2m² – 35 = 0

$\Leftrightarrow$ 2m² + 14m = 0

$\Leftrightarrow$ 2m(m + 7) = 0

$\Leftrightarrow [\begin{array}{l} m = 0 \\ m + 7 = 0 \end{array}$ $\Leftrightarrow [\begin{array}{l} m = 0 \\ m = - 7 \end{array}$

Vậy m = 0 hoặc m = -7 thì phương trình có nghiệm x = -7

Câu 4:

Tìm m để phương trình (2m – 5)x – 2m² – 7 = 0 nhận x = -3 làm nghiệm

A. m = 1 hoặc m = 4

B. m = -1 hoặc m = -4

C. m = -1 hoặc m = 4

D. m = 1 hoặc m = -4

Xem đáp án

Đáp án cần chọn là: D

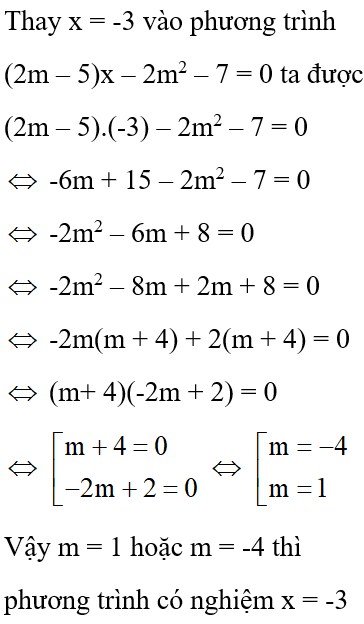
Câu 5:

Tập nghiệm của phương trình (5x² – 2x + 10)² = (3x² +10x – 8)²là:

A. S = { $\frac{1}{2}$ ; 3}

B. S = { $\frac{1}{2}$ ; -3}

C. S = {- $\frac{1}{2}$ ; 3}

D. S = {- $\frac{1}{2}$ ; -3}

Xem đáp án

Đáp án cần chọn là: C

(5x² – 2x + 10)² = (3x² +10x – 8)²

$\Leftrightarrow$ (5x² – 2x + 10)² - (3x² +10x – 8)² = 0

$\Leftrightarrow$ (5x² – 2x + 10 + 3x² +10x – 8)(5x² – 2x + 10 – 3x² – 10x + 8) = 0

$\Leftrightarrow$ (8x² + 8x + 2)(2x² – 12x + 18) = 0

$\Leftrightarrow [\begin{array}{l} 8 x^{2} + 8 x + 2 = 0 \\ 2 x^{2} - 12 x + 18 = 0 \end{array}$ $\Leftrightarrow [\begin{array}{l} 2 {(2 x + 1)}^{2} = 0 \\ 2 {(x - 3)}^{2} = 0 \end{array}$

$\Leftrightarrow [\begin{array}{l} 2 x + 1 = 0 \\ x - 3 = 0 \end{array}$ $\Leftrightarrow [\begin{array}{l} x = - \frac{1}{2} \\ x = 3 \end{array}$

Vậy phương trình có tập nghiệm: S = {-; 3}

Câu 6:

Số nghiệm của phương trình (5x² – 2x + 10)³ = (3x² +10x – 6)³là:

A. 1

B. 2

C. 3

D. 0

Xem đáp án

Đáp án cần chọn là: B

(5x² – 2x + 10)³ = (3x² +10x – 6)³

$\Leftrightarrow$ 5x² – 2x + 10 = 3x² +10x – 6

$\Leftrightarrow$ 5x² – 3x² – 2x – 10x + 10 + 6 = 0

$\Leftrightarrow$ 2x² – 12x + 16 = 0

$\Leftrightarrow$ x² – 6x + 8 = 0

$\Leftrightarrow$ x² – 4x – 2x + 8 = 0

$\Leftrightarrow$ x(x – 4) – 2(x – 4) = 0

$\Leftrightarrow$ (x – 2)(x – 4) = 0

$\Leftrightarrow [\begin{array}{l} x - 2 = 0 \\ x - 4 = 0 \end{array}$ $\Leftrightarrow [\begin{array}{l} x = 2 \\ x = 4 \end{array}$

Vậy phương trình có 2 nghiệm

Câu 7:

Biết rằng phương trình (x² – 1)² = 4x + 1 có nghiệm lớn nhất là x₀. Chọn khẳng định đúng

A. x₀ = 3

B. x₀ < 2

C. x₀ > 1

D. x₀ < 0

Xem đáp án

Đáp án cần chọn là: C

Ta có (x² – 1)² = 4x + 1 $\Leftrightarrow$ x⁴ – 2x² + 1 = 4x + 1

$\Leftrightarrow$ x⁴ – 2x² + 1 + 4x² = 4x² + 4x + 1 (Cộng 4x² vào hai vế)

$\Leftrightarrow$ (x² + 1)² = (2x + 1)²

$\Leftrightarrow [\begin{array}{l} x^{2} + 1 = 2 x + 1 \\ x^{2} + 1 = - 2 x - 1 \end{array}$

$\Leftrightarrow [\begin{array}{l} x^{2} - 2 x = 0 \\ x^{2} + 2 x + 2 = 0 \end{array}$

$\Leftrightarrow [\begin{array}{l} x (x - 2) = 0 \\ {(x + 1)}^{2} + 1 = 0 (V N) \end{array}$

$\Leftrightarrow [\begin{array}{l} x = 0 \\ x = 2 \end{array}$

Vậy S = {0; 2}, nghiệm lớn nhất là x₀ = 2 > 1

Câu 8:

Biết rằng phương trình (4x² – 1)² = 8x + 1 có nghiệm lớn nhất là x₀. Chọn khẳng định đúng

A. x₀ = 3

B. x₀ < 2

C. x₀ > 1

D. x₀ < 0

Xem đáp án

Đáp án cần chọn là: B

Cộng 16x² vào hai vế của phương trình đã cho ta được

(4x² – 1)² +16x² = 16x² + 8x + 1

$\Leftrightarrow$ 16x⁴ – 8x² + 1 + 16x² = 16x² + 8x + 1

$\Leftrightarrow$ (4x² + 1)² = (4x + 1)²

$\Leftrightarrow$ (4x² + 1 + 4x + 1)(4x² + 1 – 4x – 1) = 0

$\Leftrightarrow$ (4x² + 4x + 2)(4x² – 4x) = 0

$\Leftrightarrow [\begin{array}{l} 4 x^{2} + 4 x + 2 = 0 \\ 4 x^{2} - 4 x = 0 \end{array}$

$\Leftrightarrow [\begin{array}{l} (4 x^{2} + 4 x + 1) + 1 = 0 \\ 4 x (x - 1) = 0 \end{array}$

$\Leftrightarrow [\begin{array}{l} ({2 x + 1)}^{2} + 1 = 0 (V N) \\ x = 0 \\ x - 1 = 0 \end{array}$ $\Leftrightarrow [\begin{array}{l} x = 0 \\ x = 1 \end{array}$

Vậy S = {0; 1}, nghiệm lớn nhất là x₀ = 1 < 2

Câu 9:

Cho phương trình (1): x(x² – 4x + 5) = 0 và phương trình (2): (x² – 1)(x² + 4x + 5) = 0.

Chọn khẳng định đúng

A. Phương trình (1) có một nghiệm, phương trình (2) có hai nghiệm

B. Phương trình (1) có hai nghiệm, phương trình (2) có một nghiệm

C. Hai phương trình đều có hai nghiệm

D. Hai phương trình đều vô nghiệm

Xem đáp án

Đáp án cần chọn là: A

Vậy phương trình (2) có hai nghiệm x = -1; x = 1

Câu 10:

Cho phương trình x⁴ – 8x²+ 16 = 0. Chọn khẳng định đúng

A. Phương trình có hai nghiệm đối nhau

B. Phương trình vô nghiệm

C. Phương trình có một nghiệm duy nhất

D. Phương trình có 4 nghiệm phân biệt

Xem đáp án

Đáp án cần chọn là: A

Ta có x⁴ – 8x²+ 16 = 0

$\Leftrightarrow$ (x²)² – 2.4.x² + 4² = 0 $\Leftrightarrow$ (x² – 4)² = 0

$\Leftrightarrow$ x² – 4 = 0 $\Leftrightarrow$ (x – 2)(x + 2) = 0

$\Leftrightarrow [\begin{array}{l} x - 2 = 0 \\ x + 2 = 0 \end{array}$ $\Leftrightarrow [\begin{array}{l} x = 2 \\ x = - 2 \end{array}$

Vậy phương trình có hai nghiệm phân biệt đối nhau

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Phương trình tích có đáp án

Trắc nghiêm Phương trình tích có đáp án (Vận dụng)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương