Bài tập: Thứ tự trong tập hợp các số nguyên chọn lọc, có đáp án
-
501 lượt thi
-
29 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Chọn câu đúng
 Xem đáp án
Xem đáp án
Đáp án là D
• Điểm 2 nằm bên trái điểm 3 nên 2 < 3. Do đó A sai.
• Điểm 3 nằm bên phải điểm -2 nên 3 > -2. Do đó B sai.
• Điểm 0 nằm bên phải điểm -3 nên 0 > -3. Do đó C sai.
• Điểm -4 nằm bên trái điểm -3 nên -4 < -3. Do đó D đúng.
Câu 2:
Chọn câu sai:
 Xem đáp án
Xem đáp án
Đáp án là D
• Điểm -5 nằm bên trái điểm -2 nên -5 < -2. Do đó A đúng.
• Điểm 0 nằm bên trái điểm 4 nên 0 < 4. Do đó B đúng.
• Điểm 0 nằm bên phải điểm -1 nên 0 > -1. Do đó C đúng.
• Điểm -5 nằm bên phải điểm -6 nên -5 > -6. Do đó D sai.
Câu 6:
Sắp xếp các số sau theo thứ tự giảm dần: 0; -2; 5; 7; -1; -8
 Xem đáp án
Xem đáp án
Đáp án là B
Các số trên được biểu diễn trên trục số theo chiều từ trái sang phải là: - 8; - 2; - 1; 0; 5; 7
Do đó, số nằm bên trái sẽ nhỏ hơn số nằm ở bên phải
Vậy dãy số trên theo thứ tự giảm dần là: 7; 5; 0; - 1; - 2; - 8
Câu 7:
Chọn đáp án đúng:
 Xem đáp án
Xem đáp án
Đáp án là D
Ta có: |-5| = 5; |-4| = 4; |0| = 0; |5| = 5; |4| = 4
⇒ |-5| > |-4| đáp án A sai
|-5| > |0| ⇒ đáp án B sai
|5| > |4| ⇒ đáp án C sai
|-5| = |5| ⇒ đáp án D đúng
Câu 8:
Trong các khẳng đinh sau, khẳng định nào đúng?
 Xem đáp án
Xem đáp án
Đáp án là C
Số nguyên lớn hơn – 1 là : 0; 1; 2; 3; …. Nhưng số 0 không là số nguyên dương. Do đó, đáp án A sai
Số nguyên nhỏ hơn 1 là: 0; -1; -2; -3; …. Nhưng số 0 không là số nguyên âm. Do đó, đáp án B sai.
Giá trị tuyệt đối của một số là khoảng cách từ số đó đến điểm 0. Vậy số có giá trị tuyệt đối nhỏ hơn sẽ gần điểm 0 hơn. Vậy trong hai số nguyên âm, số nào có giá trị tuyệt đối nhỏ hơn sẽ nằm ở bên phải nên nó lớn hơn. Đáp án C đúng.
Giá trị tuyệt đối của một số nguyên dương bằng chính nó. Do đó, đáp án D sai
Câu 10:
Số đối của các số nguyên -2; 7; |-8|; |10|; 16
 Xem đáp án
Xem đáp án
Đáp án là D
Ta có: số đối của – 2 là 2; số đối của 7 là – 7 ; số đối của 16 là – 16
|-8| = 8 nên số đối của |-8| là – 8
|10| = 10 nên số đối của |10| là – 10
Câu 11:
Biết - 9 < x < 0. Tập hợp các số nguyên x thỏa mãn:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Vì−9<x<0;x∈Z⇒x∈{−8; −7; −6; −5; −4; −3; −2; −1}
Do đó A={−8; −7; −6; −5; −4; −3; −2; −1}
Câu 12:
Biết - 8 < x < - 2. Tập hợp các số nguyên x thỏa mãn là:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Vì−8<x<−2;x∈Z⇒x∈{−7;−6;−5;−4;−3}
Do đó A={−7;−6;−5;−4;−3}
Câu 13:
Viết tập hợp M ={x∈ Z| } dưới dạng liệt kê ta được
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: C
Các số nguyên lớn hơn −5 và nhỏ hơn hoặc bằng 3 là −4;−3;−2;−1;0;1;2;3.
Nên M={−4;−3;−2;−1;0;1;2;3}.
Câu 14:
Viết tập hợp M = N ={x∈ Z*| } dưới dạng liệt kê ta được
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: C
Các số nguyên khác 0 lớn hơn hoặc bằng −4 và nhỏ hơn hoặc bằng 5 là −4;−3;−2;−1;1;2;3;4;5
Nên M={−4;−3;−2;−1;1;2;3;4;5}.
Câu 15:
Số liền trước của số đối của số 11 là
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Số đối của số 11 là: −11
Số liền trước của −11 là: −12
Câu 16:
Số đối của số liền trước số - 34 là
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Số liền trước của −34 là: −35
Số đối của số −35 là: 35
Câu 17:
Số nguyên âm lớn nhất có 6 chữ số là
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: C
Số nguyên dương nhỏ nhất có 6 chữ số là: 100000
Nên số nguyên âm lớn nhất có 6 chữ số là: −100000
Câu 18:
Số nguyên âm bé nhất có 5 chữ số là
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: C
Số nguyên dương lớn nhất có 5 chữ số là: 99999
Nên số nguyên âm bé nhất có 5 chữ số là: −99999
Câu 19:
Kết quả của phép tính |345|:|−5|+|−25| là số
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
Ta có |345|:|−5|+|−25|=345:5+25=94.
Vậy kết quả phép tính là một số nguyên dương.
Câu 20:
Kết quả của phép tính |−657|:|9|+|−27| là số
 Xem đáp án
Xem đáp án
Đáp án cần chọn là : B
Ta có|−657|:|9|+|−27|=657:9+27=73+27=100
Vậy kết quả phép tính là một số nguyên dương
Câu 23:
Có bao nhiêu số nguyên x sao cho 6<|x|≤9
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: D
Ta có: 6<|x|≤9⇒|x|∈{7;8;9}
Vì x∈Z nên x∈{±7;±8;±9}
Vậy x∈{±7;±8;±9}
Có 6 số nguyên thỏa mãn điều kiện đề bài.
Câu 24:
Có bao nhiêu số nguyên x sao cho 11<|x|≤22
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: D
Ta có:11<|x|≤22 ⇒|x|∈{12; 13; 14; 15; 16; 17; 18; 19; 20; 21; 22}
Vì x∈Z nênx∈{±12;±13;±14;±15;±16;±17;±18;±19;±20;±21;±22}.
Vậyx∈{±12; ±13; ±14; ±15; ±16; ±17; ±18; ±19; ±20; ±21; ±22}.
Có 22 số nguyên thỏa mãn điều kiện đề bài.
Câu 25:
Cho x ∈ Z. Tìm giá trị nhỏ nhất của biểu thức P=|x|+10
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Ta có: P=|x|+10
Vì |x|≥0 với mọi x∈Z nên |x|+10≥10 với mọi x∈Z hay P≥10 với mọi x∈Z
Dấu bằng xảy ra khi x=0
Vậy giá trị nhỏ nhất của P bằng 10.
Câu 26:
Cho x ∈ Z. Tìm giá trị nhỏ nhất của biểu thức P=|x|+20
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Ta có: P=|x|+20
Vì |x|≥0 với mọi x∈Z nên |x|+20≥20với mọi x∈Z hay P≥20 với mọi x∈Z
Dấu bằng xảy ra khi x=0.
Vậy giá trị nhỏ nhất của P bằng 20.
Câu 27:
Tìm x ∈ Z biết |x|<5
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
|x|<5
Suyra−5<x<5
Vậy x∈{−4;−3;−2;−1;0;1;2;3;4}
Câu 28:
Tìm x biết |6| . |x| = |-36|
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: D
|6| . |x| = |-36|
|6| . |x| = 36
|x| = 6
TH1: x=6
TH2: x=−6
Câu 29:
Tìm a;b thuộc Z biết |a|+|b|0
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Ta có
|a|+|b|≥0 với mọi a,b
Do đó để |a|+|b| 0 khi và chỉ khi |a|=0;|b|=0
Nên a=0;b=0

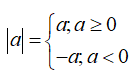 nên đáp án C. |a| = a nếu a ≥ 0 là đáp án đúng.
nên đáp án C. |a| = a nếu a ≥ 0 là đáp án đúng.