Bài tập: Tính chất chia hết của một tổng chọn lọc, có đáp án
-
553 lượt thi
-
18 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Nếu a không chia hết cho 2 và b chia hết cho 2 thì tổng a + b
Xem đáp án
Đáp án là B
Theo tính chất 2: Nếu a không chia hết cho 2 và b chia hết cho 2 thì a + b không chia hết cho 2
Câu 2:
Tổng nào sau đây chia hết cho 7
Xem đáp án
Đáp án là A
Theo tính chất 1: Ta có 49 chia hết cho 7 và 70 chia hết cho 7 nên 49 + 70 chia hết cho 7.
Câu 3:
Nếu x ⋮ 2 và y ⋮ 4 thì tổng x + y chia hết cho?
Xem đáp án
Đáp án là A
Ta có: y ⋮ 4 ⇒ y ⋮ 2
x ⋮ 2 và y ⋮ 2 ⇒ (x + y) ⋮ 2
Câu 5:
Chọn câu sai
Xem đáp án
Đáp án là C
Ta có: 18 ⋮ 9; 54 ⋮ 9; 12 không chia hết 9 ⇒ (18 + 54 + 12) không chia hết 9
Đáp án C sai.
Câu 6:
Có tổng M = 75 + 120 + x. Với giá trị nào của x dưới dây thì M ⋮ 3?
Xem đáp án
Đáp án là D
Ta có: 75 ⋮ 3; 120 ⋮ 3. Vậy để M ⋮ 3 thì x ⋮ 3
Trong bốn đáp án ta thấy chỉ có x = 12 thỏa mãn điều kiện
Do đó giá trị cần tìm là x = 12
Câu 7:
Tìm số tự nhiên x để A = 75 + 1003 + x chia hết cho 5
Xem đáp án
Đáp án là C
Ta thấy 75 chia hết cho 5 và 1003 không chia hết cho 5
Nên để A = 75 + 1003 + x chia hết cho 5 thì (1003 + x) chia hết cho 5
Mà 1003 chia cho 5 dư 3 nên để (1003 + x) chia hết cho 5 thì x chia cho 5 dư 2
Câu 8:
Cho A = 12 + 15 + 36 + x, x ∈ ℕ. Tìm điều kiện của x để A không chia hết cho 9.
Xem đáp án
Đáp án là B
Ta có: A = (12 + 15) + 36 + x
Vì 12 + 15 = 27 ⋮ 9; 36 ⋮ 9 ⇒ (12 + 15 + 36) ⋮ 9
Do đó để A không chia hết cho 9 thì x không chia hết cho 9
Câu 9:
Trong các khẳng định sau, khẳng định nào sai?
Xem đáp án
Đáp án là B
Dựa vào các tính chất chia hết ta thấy đáp án A, C, D đúng
Đáp án B sai. Ví dụ:
Ta có: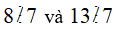 
nhưng 8 + 13 = 21 ⋮ 7
Câu 10:
Khi chia số tự nhiên a cho 12, ta được số dư là 8. Khẳng định nào sau đây đúng?
Xem đáp án
Đáp án là B
Số tự nhiên a chia cho 12 được số dư là 8 nên a = 12k + 8, k ∈ ℕ
Ta có: 12k ⋮ 4; 8 ⋮ 4 ⇒ 12k + 8 ⋮ 4
Câu 11:
Cho với k > 1. Khi đó chia hết cho số nào dưới đây?
Xem đáp án
Đáp án cần chọn là: D
Ta có:
Vậy M19
Câu 12:
Khi chia số a cho 12 ta được số dư là 9. Khi đó:
Xem đáp án
Đáp án cần chọn là: B
Vì a chia cho 12 được số dư là 9 nên a=12k+9(k∈N)
Vì 12k⋮3;9⋮3⇒a=(12k+9)⋮3
Và 12k⋮4;9 không chia hết cho 4 nên a=12k+9 không chia hết cho 4.
Vậy a chia hết cho 3 nhưng không chia hết cho 4.
Câu 13:
Với a,b là các số tự nhiên, nếu 10a + b chia hết cho 13 thì a + 4b chia hết cho số nào dưới đây?
Xem đáp án
Đáp án cần chọn là: D
Xét 10.(a+4.b)=10.a+40.b=(10.a+b)+39.b .
Vì (10.a+b)⋮13 và 39b⋮13 nên 10.(a+4.b)⋮13 .
Do 10 không chia hết cho 13 nên suy ra (a+4.b)⋮13 .
Vậy nếu 10a+b chia hết cho 13 thì a+4b chia hết cho 13
Câu 14:
Với a,b là các số tự nhiên, nếu 11a + 2b chia hết cho 8 thì a + 6b chia hết cho số nào dưới đây?
Xem đáp án
Đáp án cần chọn là: A
Xét 11.(a+6.b)=11.a+66.b=(11.a+2b)+64.b
Vì (11.a+2b)⋮8 và 64b⋮8 nên 11.(a+6.b)⋮8.
Do 11 không chia hết cho 8 nên suy ra (a+6.b)⋮8.
Vậy nếu 11a+2b chia hết cho 8 thì a+6b chia hết cho 8.
Câu 15:
Có bao nhiêu số tự nhiên n để (n + 7) chia hết cho (n + 2)?
Xem đáp án
Đáp án cần chọn là: C
Vì (n+2)⋮(n+2) nên theo tính chất 1 để (n+7)⋮(n+2) thì [(n+7)−(n+2)]⋮(n+2) hay 5⋮(n+2) .
Suy ra (n+2)∈{1;5} .
Vì n+2≥2 nên n+2=5⇒n=5–2=3.
Vậy n=3.
Vậy có một số tự nhiên n thỏa mãn yêu cầu.
Câu 16:
Có bao nhiêu số tự nhiên n để (n + 9) chia hết cho (n + 5) ?
Xem đáp án
Đáp án cần chọn là: D
Vì (n+5)⋮(n+5) nên theo tính chất 1 để (n+9)⋮(n+5) thì [(n+9)−(n+5)]⋮(n+5) hay 4⋮(n+5).
Suy ra (n+5)∈{1;2;4}.
Vì n+5≥5 nên không có giá trị của n thỏa mãn.
Câu 17:
Chọn câu sai.
Xem đáp án
Đáp án cần chọn là: D
+) Gọi ba số tự nhiên liên tiếp là n; n+1; n+2 (n∈N) thì tổng ba số tự nhiên liên tiếp là n+n+1+n+2=3n+3. Vì 3⋮3 nên (3n+3)⋮3 suy ra A đúng.
+) Gọi bốn số tự nhiên liên tiếp là n;n+1;n+2;n+3 (n∈N) thì tổng bốn số tự nhiên liên tiếp là n+n+1+n+2+n+4=4n+7. Vì 4n⋮4;7⋮̸4 nên (4n+7)⋮̸4 suy ra B đúng, D sai.
+) Gọi năm số tự nhiên chẵn liên tiếp là 2n; 2n+2; 2n+4; 2n+6; 2n+8 (n∈N) thì tổng năm số tự nhiên chẵn liên tiếp là 2n+2n+2+2n+4+2n+6+2n+8=10n+20. Vì 10n⋮10;20⋮10 nên (10n+20)⋮10 suy ra C đúng.
