Đề kiểm tra Giữa học kì 1 Toán 6 có đáp án
-
751 lượt thi
-
12 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
I. Phần trắc nghiệm (4 điểm)
Tập hợp A các số tự nhiên nhỏ hơn 7 được viết là:
Xem đáp án
Gọi x là số tự nhiên thuộc tập hợp A.
Ta có x là số tự nhiên nên x \( \in \mathbb{N}\)
Mà các số tự nhiên thuộc tập hợp A nhỏ hơn 7 nên x < 7.
Vậy ta viết tập hợp A như sau: A = {x \( \in \mathbb{N}\)| x < 7}.
Chọn đáp án B.
Câu 2:
Xem đáp án
Ta có: B = {1; 8; 12; 21}
Nhận thấy số 18 không phải là phần tử của tập hợp B nên 18 không thuộc tập hợp B.
Chọn đáp án D.
Câu 3:
Xem đáp án
Lý thuyết: Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có hai ước là 1 và chính nó.
Hợp số là số tự nhiên lớn hơn 1, có nhiều hơn hai ước. Một số là hợp số thì không thể là số nguyên tố.
Trong các số đã cho, ta thấy:
+) 114 có chữ số tận cùng là 4 nên nó chia hết cho 2, do đó 114 là hợp số vì ngoài hai ước là 1 và 114 thì nó còn có thêm ít nhất một ước nữa là 2.
+) 305 có chữ số tận cùng là 5 nên nó chia hết cho 5, do đó 305 là hợp số vì ngoài hai ước là 1 và 305 thì nó còn có thêm ít nhất một ước nữa là 5.
+) 303 có tổng các chữ số là 3 + 0 + 3 = 6 chia hết cho 3 nên nó chia hết cho 3, do đó 303 là hợp số vì ngoài hai ước là 1 và 303 thì nó còn có thêm ít nhất một ước nữa là 3.
+) Số 101 lớn hơn 1, chỉ có hai ước là 1 và 101 nên nó là số nguyên tố.
Chọn đáp án A.
Câu 4:
Xem đáp án
Các số 120, 195, 215, 300 đều chia hết cho 5 (vì có tận cùng là 0 hoặc 5).
Số 215 có tổng các chữ số là 2 + 1 + 5 = 8 không chia hết cho 3 nên 215 không chia hết cho 3.
Vậy số 215 chia hết cho 5 nhưng không chia hết cho 3.
Chọn đáp án C.
Câu 5:
Xem đáp án
Ta có: a = 4 . 5 + 22 . (8 – 3) = 20 + 4 . 5 = 20 + 20 = 40 (cm)
Diện tích hình vuông có cạnh a là:
S = a . a = 40 . 40 = 1 600 (cm2).
Chọn đáp án D.
Câu 6:
Xem đáp án
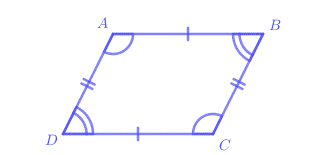
Hình bình hành ABCD có các tính chất:
+ Hai cạnh đối AB và CD, AD và BC song song với nhau.
+ Hai cạnh đối AB và CD, AD và BC bằng nhau.
+ Hai góc ở đỉnh A và C bằng nhau, hai góc ở đỉnh B và D bằng nhau (hai góc đối bằng nhau)
Do đó hình bình hành không có tính chất: Bốn cạnh bằng nhau.
Chọn đáp án D.
Câu 7:
Xem đáp án
Ta có: x là số tự nhiên thỏa mãn 3 ≤ x < 8
Khi đó: x \( \in \){3; 4; 5; 6; 7}
Lại có: 24 ⁝ (x + 6) (*)
Ta thử thay lần lượt các giá trị của x vào (*), ta thấy x = 6 thỏa mãn vì x + 6 = 6 + 6 = 12, 24 chia hết cho 12.
Vậy x có giá trị là 6.
Chọn đáp án B.
Câu 8:
Xem đáp án
Diện tích hình thoi bằng \(\frac{1}{2}\)lần tích độ dài hai đường chéo.
Do đó diện tích hình thoi có độ dài hai đường chép bằng 8 cm và 10 cm là:
S = \(\frac{1}{2}.8.10\) = 40 (cm2)
Chọn đáp án A.
Câu 9:
II. Phần tự luận (6 điểm)
Thực hiện phép tính:
a) 162 + 475 + 173 + 227 + 525 + 438;
b) 25 . 6 + 5 . 5 . 29 – 45 . 5;
c) 2 . [(7 – 33 : 32) : 22 + 99] – 100;
d) (52022 + 52021) : 52021.
Xem đáp án
a) 162 + 475 + 173 + 227 + 525 + 438
= (162 + 438) + (475 + 525) + (173 + 227)
= 600 + 1 000 + 400
= (600 + 400) + 1 000
= 1 000 + 1 000
= 2 000
b) 25 . 6 + 5 . 5 . 29 – 45 . 5
= 25 . 6 + 25 . 29 – 9 . 5 . 5
= 25 . 6 + 25 . 29 – 25 . 9
= 25 . (6 + 29 – 9)
= 25 . 26 = 650
c) 2 . [(7 – 33 : 32) : 22 + 99] – 100
= 2 . [(7 – 3) : 4 + 99] – 100
= 2 . [4 : 4 + 99] – 100
= 2 . (1 + 99) – 100
= 2 . 100 – 100 = 100
d) (52 022 + 52 021) : 52 021
= 52 022 : 52 021 + 52 021 : 52 021
= 52 022 – 2 021 + 52 021 – 2 021
= 51 + 50
= 5 + 1 = 6
Câu 10:
Xem đáp án
Nửa chu vi của hình chữ nhật là: 140 : 2 = 70 (m)
Chiều rộng mảnh vườn hình chữ nhật là: 70 – 40 = 30 (m)
Diện tích mảnh vườn hình chữ nhật là: 40 . 30 = 1 200 (m2).
Câu 11:
Xem đáp án
Gọi số hàng có thể xếp là x (x \( \in {\mathbb{N}^*}\); hàng)
Theo đề bài có: 42 ⁝ x; 54 ⁝ x; 48 ⁝ x và x lớn nhất nên x là ƯCLN của 42, 54 và 48.
Ta tìm ƯCLN này bằng cách phân tích các số 42, 54, 48 ra thừa số nguyên tố.
Ta có: 42 = 2 . 3 . 7
54 = 2 . 33
48 = 24 . 3
Suy ra ƯCLN(42, 54, 48) = 2 . 3 = 6 hay x = 6 (thỏa mãn).
Vậy có thể xếp được nhiều nhất là 6 hàng để thỏa mãn yêu cầu bài toán.
Câu 12:
Xem đáp án
Có 1028 có dạng 10….000 (28 chữ số 0) nên 1028 + 8 có dạng 10….008 (27 chữ số 0) nên số 1028 + 8 sẽ chia hết cho 9 (tổng các chữ số bằng 9).