Bài tập chuyên đề Toán 6 Hình bình hành có đáp án
-
651 lượt thi
-
19 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
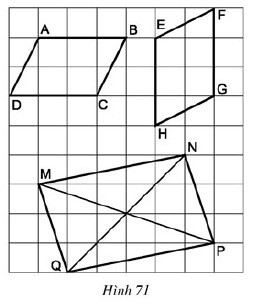
Xem đáp án
Lời giải
Cả ba tứ giác là hình bình hành
- Tứ giác ABCD là hình bình hành vì có AB // CD và AB = CD = 3 (dấu hiệu nhận biết 3)
- Tứ giác EFGH là hình bình hành vì có EH // FG và EH = FH = 3 (dấu hiệu nhận biết 3)
- Tứ giác MNPQ là hình bình hành vì có MN = PQ và MQ = NP (dấu hiệu nhận biết 2)
Chú ý:
- Với các tứ giác ABCD, EFGH còn có thể nhận biết là hình bình hành bằng dấu hiệu nhận biết 2.
- Với tứ giác MNPQ còn có thể nhận biết là hình bình hành bằng dấu hiệu nhận biết 5.
Câu 2:
Xem đáp án
Lời giải
Câu 3:
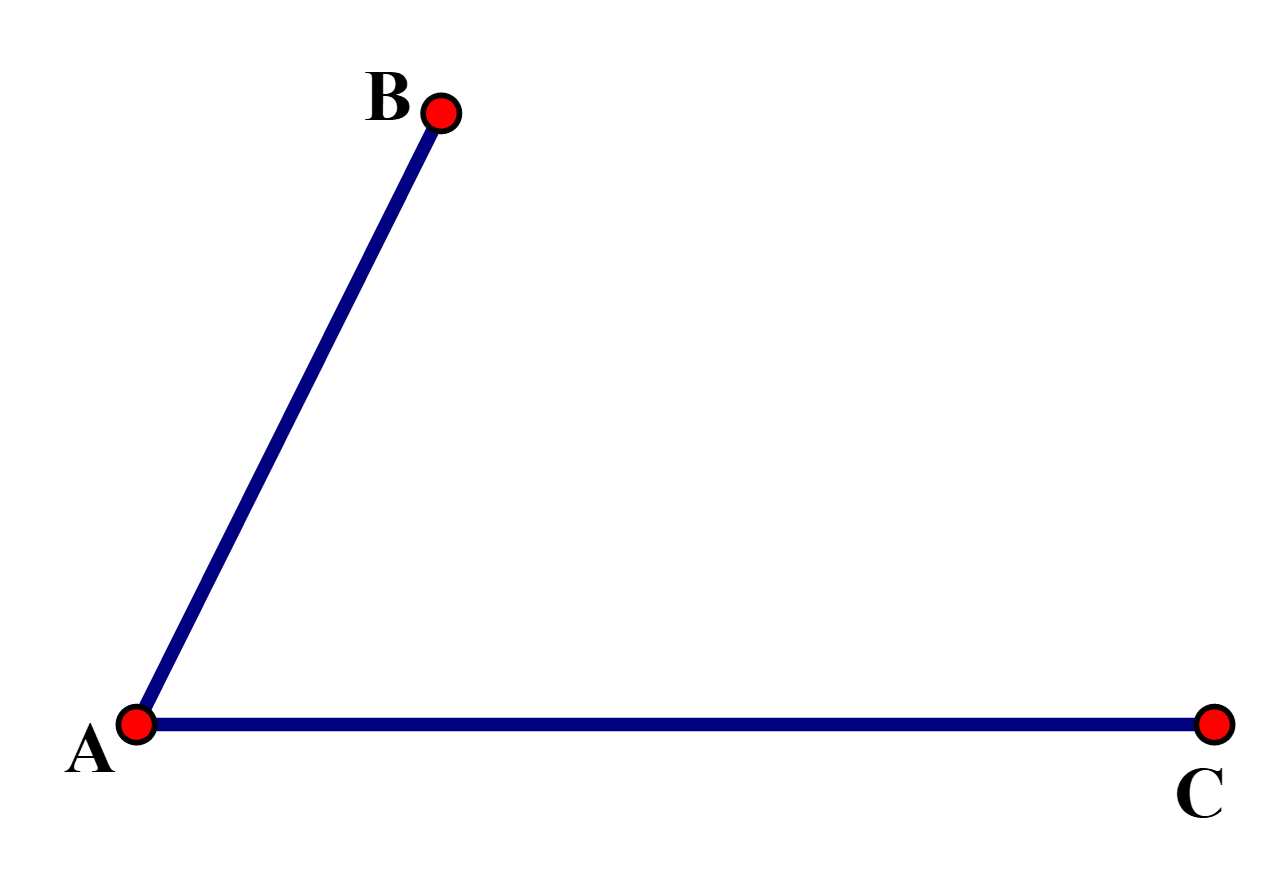
Xem đáp án
Lời giải
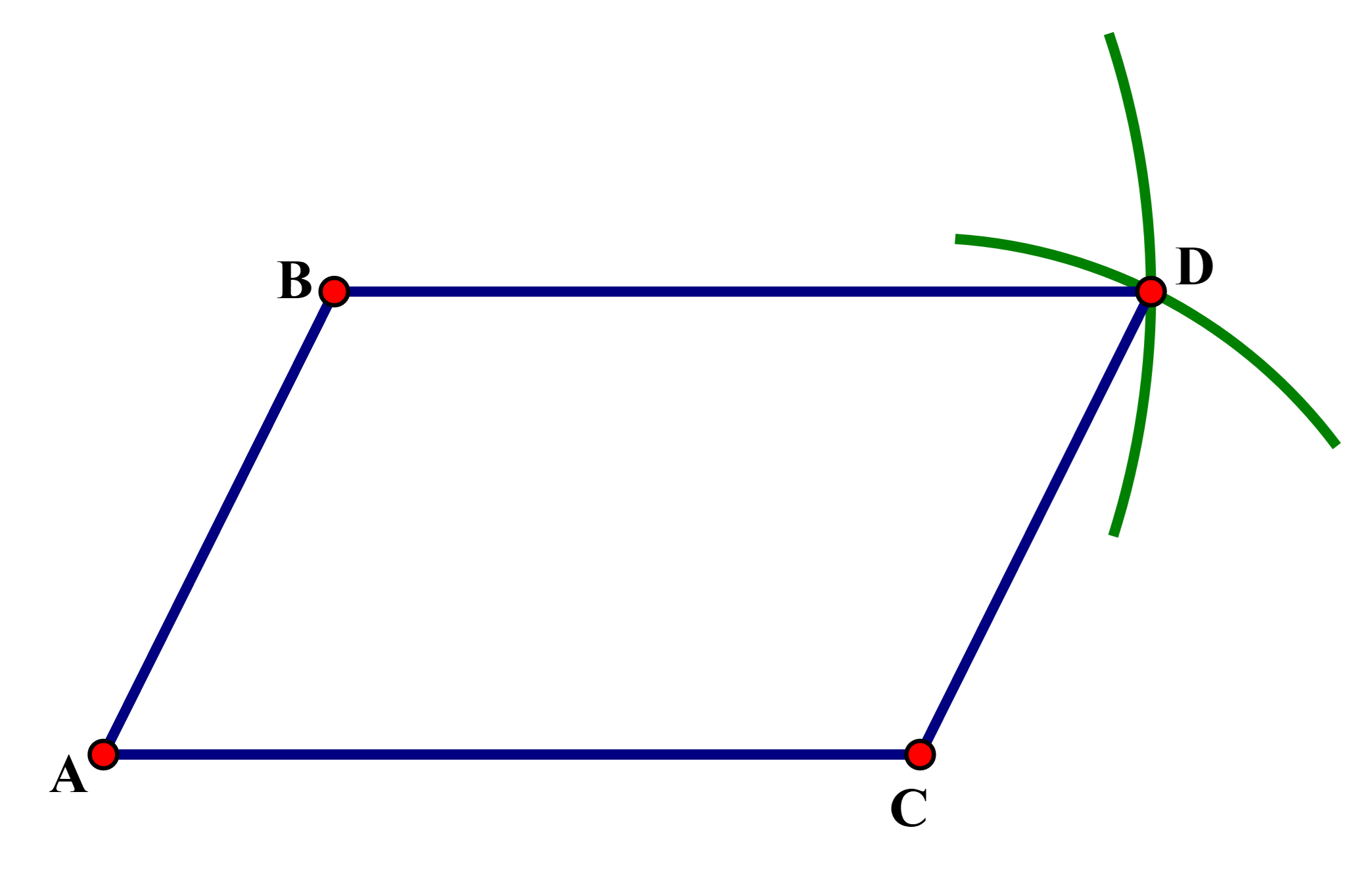
Bước 1.
- Vẽ một phần đường tròn tâm B bán kính AC.
- Vẽ một phần đường tròn tâm C bán kính AB.
Hai đườngtròn này cắt nhau tại D.
Bước 2. Nối D với B, D với C, ta được hình bình hành ABCD.
Câu 4:
Xem đáp án
Lời giải
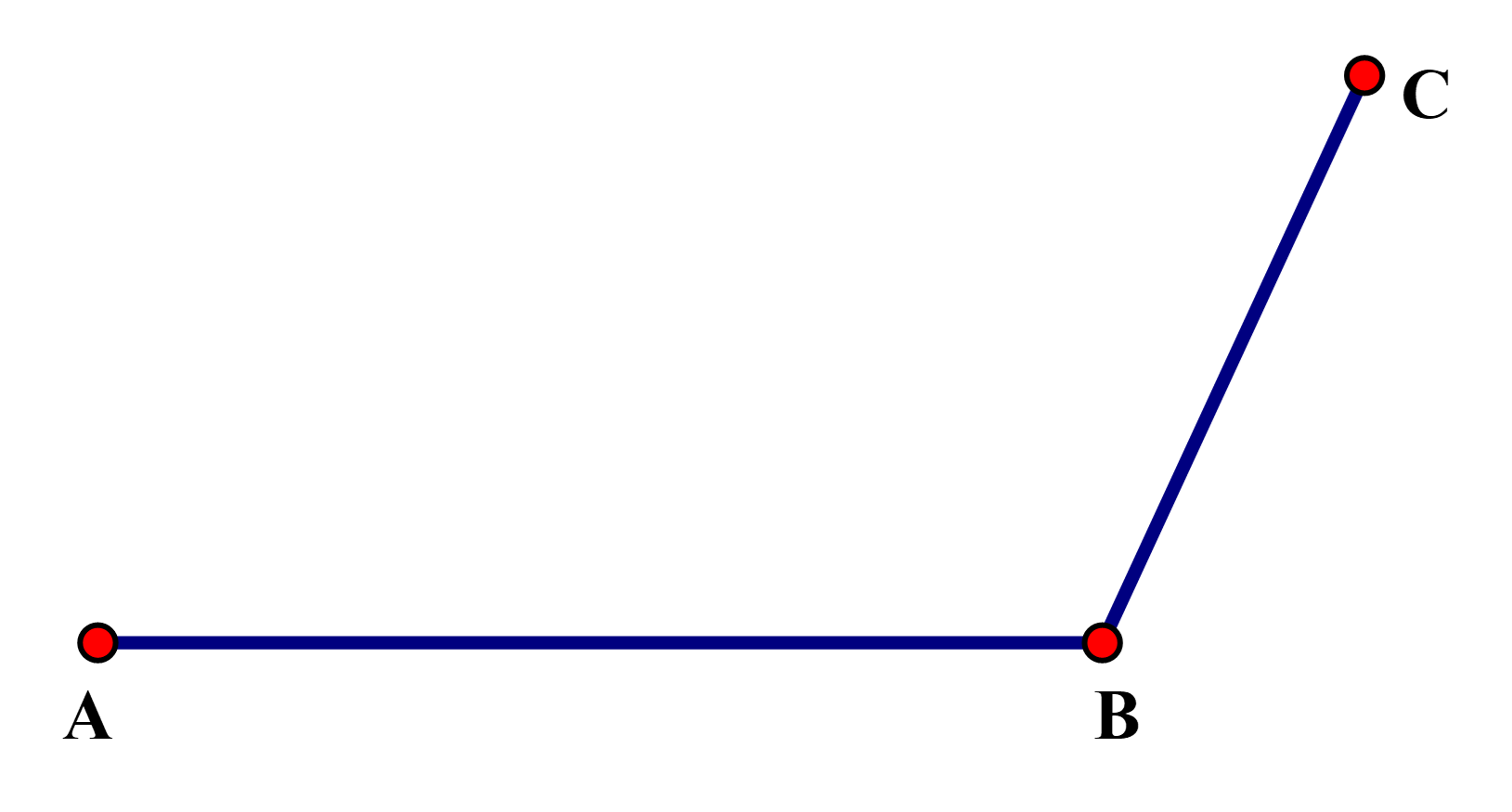
Bước 2. Vẽ đường thẳng đi qua \(B\). Trên đường thẳng đó lấy điểm \(C\) sao cho \[BC = 3cm\]
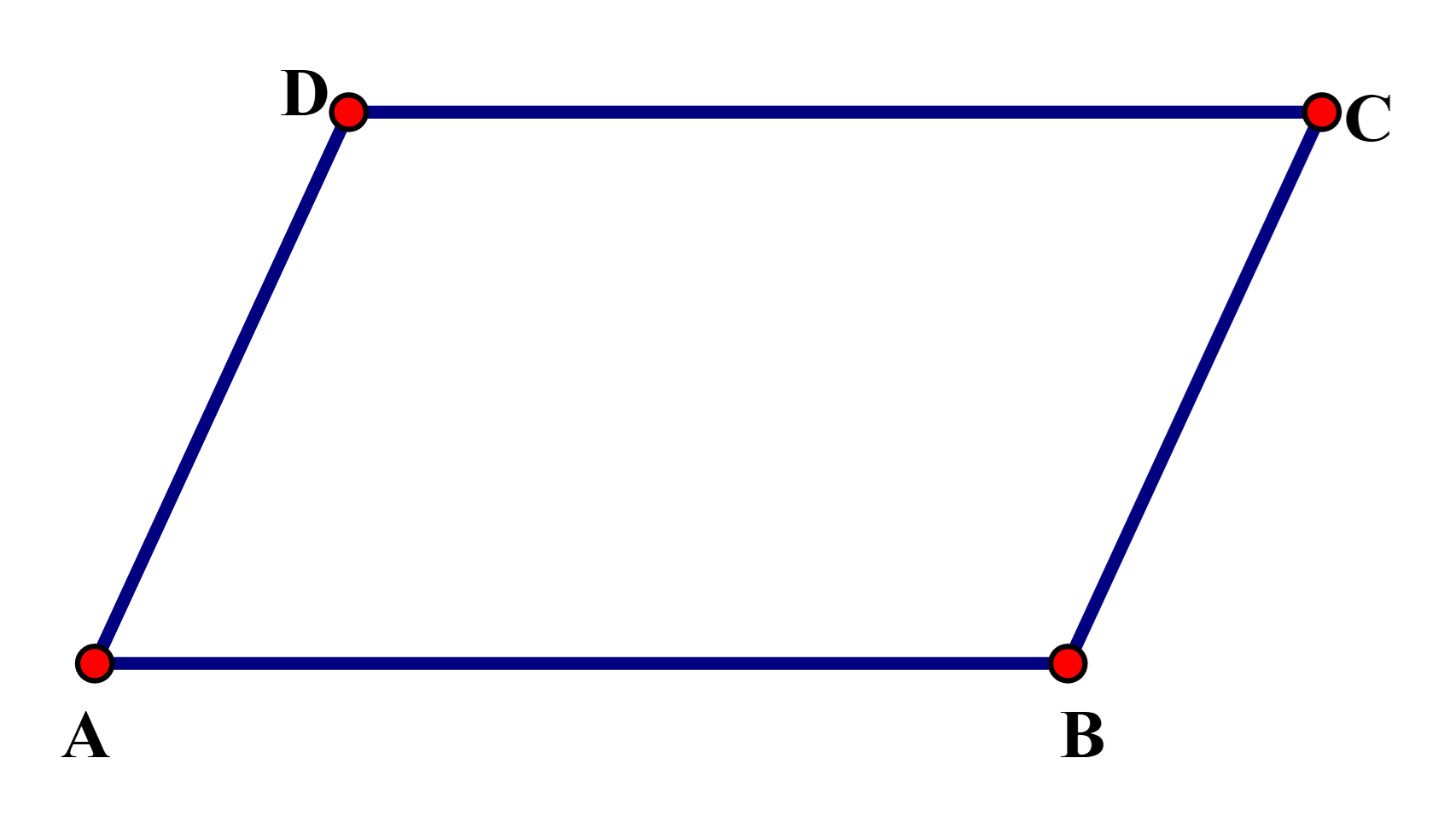
Câu 5:
Xem đáp án
Lời giải
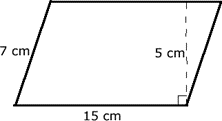
Chu vi của hình bình hành là: \[C = 2.(15 + 7) = 44{\rm{ }}(cm)\]
Diện tích hình bình hành là: \[S = 15.5 = 75{\rm{ (c}}{{\rm{m}}^2})\]
Câu 6:
Xem đáp án
Lời giải
Gọi cạnh bên \(a\), ta có: cạnh đáy \[5a\], chiều cao \(\frac{{5a}}{8}\)
Chu vi hình bình hành = (cạnh bên + cạnh đáy) x 2 = 384
suy ra \[\left( {a + 5a} \right){\rm{ x }}2 = 384\] hay \[a{\rm{ }} = {\rm{ }}30cm\]
Do đó, cạnh bên \[32cm\], cạnh đáy \[160cm\], chiều cao \(20\,cm\)
Vì thế, diện tích hình bình hành là \[20{\rm{ x }}160 = 3600{\rm{ }}\left( {c{m^2}} \right)\]
Câu 7:
Một mảnh đất hình bình hành, biết cạnh đáy bằng \[23{\rm{ m}}\], mở rộng mảnh đất bằng việc tăng cạnh đáy mảnh đất này thêm \[{\rm{5 m}}\] thì được mảnh đất hình bình hành mới có diện tích lớn hơn mảnh đất ban đầu là \[115{\rm{ }}{{\rm{m}}^2}\]. Tính diện tích mảnh đất hình bình hành ban đầu.
Xem đáp án
Lời giải
Dựa vào công thức tính diện tích hình bình hành:
- Theo đầu bài, diện tích mảnh đất hình hành mới bằng \[115{\rm{ }}{{\rm{m}}^2}\].
- Do đó, chiều cao của mảnh đất là \[115{\rm{ : 5 = 23 m}}\].
- Vì thế diện tích mảnh đất hình bình hành ban đầu là \[23.{\rm{ }}23 = 529{\rm{ }}{{\rm{m}}^2}\].
Câu 8:
Xem đáp án
Lời giải
Theo đầu bài, diện tích mảnh đất hình thoi bị cắt đi là \[15{\rm{ }}{{\rm{m}}^2}\].
Do đó, chiều cao của mảnh đất là \[15{\rm{ : 5 = 3 }}{{\rm{m}}^2}\].
Vì thế, diện tích của mảnh đất hình bình hành ban đầu là \[3.{\rm{ 27 = 81 }}{{\rm{m}}^2}\].
Câu 9:
Xem đáp án
Lời giải
Phần diện tích tăng thêm chính là diện tích hình bình hành có cạnh đáy \(7\,m\) và chiều cao là chiều cao của mảnh đất hình bình hành ban đầu.
Chiều cao mảnh đất là: \[189{\rm{ }}:{\rm{ }}7{\rm{ }} = {\rm{ }}27{\rm{ }}\left( m \right)\]
Diện tích mảnh đất hình bình hành ban đầu là: \[27{\rm{ x }}47{\rm{ }} = {\rm{ }}1269{\rm{ }}\left( {{m^2}} \right)\]
Câu 10:
Xem đáp án
Lời giải
Ta có nửa chu vi hình bình hành là: \[480{\rm{ }}:{\rm{ }}2{\rm{ }} = {\rm{ }}240{\rm{ }}\left( {cm} \right)\]
Nếu như coi cạnh kia là 1 phần thì cạnh đáy chính là 5 phần như vậy.
Ta có cạnh đáy hình bình hành là: \[240{\rm{ }}:{\rm{ }}\left( {5 + 1} \right){\rm{ x }}5{\rm{ }} = {\rm{ }}200{\rm{ }}\left( {cm} \right)\]
Tính được chiều cao của hình bình hành là: \[200{\rm{ }}:{\rm{ }}8{\rm{ }} = {\rm{ }}25{\rm{ }}\left( {cm} \right)\]
Diện tích của hình bình hành là: \[200{\rm{ x }}25{\rm{ }} = {\rm{ }}5000{\rm{ }}\left( {c{m^2}} \right)\]
Câu 11:
Xem đáp án
Lời giải
Nửa chu vi hình bình hành là: \[364{\rm{ }}:{\rm{ }}2{\rm{ }} = {\rm{ }}182{\rm{ }}\left( {cm} \right)\]
Cạnh đáy gấp 6 lần cạnh kia nên nửa chu vi sẽ gấp 7 lần cạnh kia.
Cạnh đáy hình bình hành là: \[182{\rm{ }}:{\rm{ }}7{\rm{ x }}6{\rm{ }} = {\rm{ }}156{\rm{ }}\left( {cm} \right)\]
Chiều cao hình bình hành là: \[156{\rm{ }}:{\rm{ }}2{\rm{ }} = {\rm{ }}78{\rm{ }}\left( {cm} \right)\]
Diện tích hình bình hành là: \[156{\rm{ x }}78 = 12168{\rm{ }}\left( {c{m^2}} \right)\]
Câu 12:
Xem đáp án
Lời giải
Phần diện tích giảm đi chính là diện tích hình bình hành có cạnh đáy là \(19\,cm\) và chiều cao là chiều cao mảnh đất hình bình hành ban đầu.
Chiều cao hình bình hành là: \[665{\rm{ }}:{\rm{ }}19{\rm{ }} = {\rm{ }}35{\rm{ }}\left( {cm} \right)\]
Diện tích hình bình hành đó là: \[71{\rm{ x }}35{\rm{ }} = {\rm{ }}2485{\rm{ }}\left( {c{m^2}} \right)\]
Câu 13:
Xem đáp án
Hướng dẫn giải
Đổi về cùng đơn vị đo rồi tính
Áp dụng công thức tính diện tích hình bình hành ta có: \(40.13 = 520\)\(\left( {d{m^2}} \right)\)
Câu 14:
Xem đáp án
Hướng dẫn giải
Áp dụng công thức tính diện tích hình bình hành ta có: \(14.\frac{{14}}{2} = 98\)\(\left( {{m^2}} \right)\)
Câu 15:
Xem đáp án
Hướng dẫn giải
Độ dài đáy của hình bình hành là \[\left( {24{\rm{ }} + {\rm{ }}4} \right){\rm{ }}:{\rm{ }}2 = {\rm{ }}14{\rm{ }}\left( m \right)\]
Chiều cao cua hình bình hành là \[14{\rm{ }} - {\rm{ }}4{\rm{ }} = {\rm{ }}10{\rm{ }}\left( m \right)\]
Diện tích của hình bình hành là \[14.10{\rm{ }} = {\rm{ }}140{\rm{ }}\left( {{m^2}} \right)\]
Câu 16:
Xem đáp án
Hướng dẫn giải
Chiều cao của hình bình hành \(24:6 = 4\) (cm)
Câu 17:
Xem đáp án
Hướng dẫn giải
Diện tích \(2{m^2} = 200d{m^2}\)
Chiều cao của hình bình hành \(200:20 = 10\) (dm)
Câu 18:
Xem đáp án
Hướng dẫn giải
Diện tích hình bình hành là \(6.6 = 36{m^2}\)
Dộ dài đáy của hình bình hành là \(36:4 = 9m\)
Câu 19:
Xem đáp án
Hướng dẫn giải
Diện tích mảnh vườn: \(50.40 = 2000\,{m^2}\)
Mảnh vườn trồng được cây bưởi là \(2000:4 = 500\) cây