Trắc nghiệm Ôn tập cuối chương 1 có đáp án
-
738 lượt thi
-
35 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Các phần tử của tập hợp được viết trong hai dấu ngoặc nhọn { }, cách nhau bởi dấu “:”.
Nên cách viết đúng là A = {1; 2; 3; 4}.
Chọn đáp án D.
Câu 2:
 Xem đáp án
Xem đáp án
Các phần tử của tập hợp được viết trong hai dấu ngoặc nhọn { }, cách nhau bởi dấu “:”.
Nên cách viết đúng là B = {2; 13; 45}
Vậy có 1 cách viết đúng.
Chọn đáp án A.
Câu 3:
 Xem đáp án
Xem đáp án
Các chữ cái tiếng Việt trong cụm từ “HỌC SINH” lần lượt là: H; O; C; S; I; N; H.
Mà trong tập hợp, mỗi phần tử ta chỉ liệt kê một lần, nên ta thấy trong từ “HỌC SINH” có hai chữ cái H, vậy khi viết tập hợp ta chỉ cần liệt kê một lần.
Do đó ta viết: P = {H; O; C; S; I; N}.
Chọn đáp án B.
Câu 4:
Cho hình vẽ
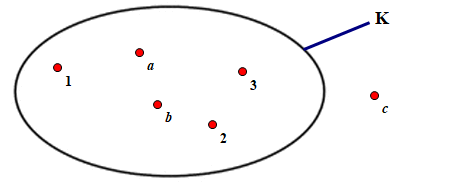
Tập hợp K là:
 Xem đáp án
Xem đáp án
Quan sát hình vẽ ta thấy các phần tử 1; 2; 3; a; b nằm trong vòng kín biểu diễn tập hợp K, nên các phần tử này thuộc tập hợp K, hơn nữa ta biểu diễn các phần tử trong tập hợp ngăn cách nhau bởi dấu “;”, do đó ta viết tập hợp K là:
K = {1; 2; 3; a; b}.
Chọn đáp án C.
Câu 5:
 Xem đáp án
Xem đáp án
Các số 0, 1, 2, 3, 4 … là các số tự nhiên.
Tập hợp các số tự nhiên được kí hiệu là 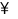 , tức là
, tức là 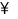 = {0; 1; 2; 3; 4; …}.
= {0; 1; 2; 3; 4; …}.
Chọn đáp án B.
Câu 6:
 Xem đáp án
Xem đáp án
Các số La Mã XV, XXI biểu diễn các số tự nhiên 15, 21 và được đọc lần lượt là: mười lăm, hai mươi mốt.
Chọn đáp án C.
Câu 7:
1 256 ; …; …
 Xem đáp án
Xem đáp án
Vì đây là dãy số tự nhiên liên tiếp giảm dần nên:
Số thứ hai là: 1 256 – 1 = 1 255
Số thứ ba là: 1 255 – 1 = 1 254
Vậy hai số cần điền là 1 255 và 1 254.
Chọn đáp án D.
Câu 8:
 Xem đáp án
Xem đáp án
Số liền trước số 99 là số 98 nên có ba số tự nhiên liên tiếp là 98; 99; 100.
Số liền sau số 100 là số 101 nên có ba số tự nhiên liên tiếp là 99; 100; 101.
Chọn đáp án D.
Câu 9:
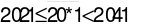 .
. Xem đáp án
Xem đáp án
Vì * là chữ số hàng chục của số 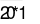 nên * nhận là các số tự nhiên từ 0 đến 9.
nên * nhận là các số tự nhiên từ 0 đến 9.
Lại có: 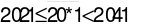
Mà số 2 021, 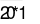 , 2 041 đều có các chữ số hàng nghìn, hàng trăm và hàng đơn vị là giống nhau. Do đó * thỏa mãn:
, 2 041 đều có các chữ số hàng nghìn, hàng trăm và hàng đơn vị là giống nhau. Do đó * thỏa mãn: 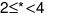
Hay * là các số tự nhiên lớn hơn hoặc bằng 2 và nhỏ hơn 4, đó là 2 và 3.
Vậy đáp án A và B đều đúng.
Chọn đáp án D.
Câu 10:
 Xem đáp án
Xem đáp án
Ta có: 53 + 25 + 47 + 75 = (53 + 47) + (25 + 75)
= 100 + 100 = 200
Chọn đáp án A.
Câu 11:
 Xem đáp án
Xem đáp án
Ta có: 418 – 18 – 100 = (418 – 18) – 100 = 400 – 100 = 300.
Chọn đáp án B.
Câu 12:
 Xem đáp án
Xem đáp án
Hiệu của 12 300 và 1 200 là kết quả của phép tính: 12 300 – 1 200.
Ta đặt tính rồi tính như sau:
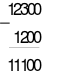
Vậy 12 300 – 1 200 = 11 110.
Chọn đáp án A.
Câu 13:
Tìm số tự nhiên x, biết: x – 124 = 567.
 Xem đáp án
Xem đáp án
Ta có: x – 124 = 567
x = 567 + 124
x = 691
Vậy x = 691.
Chọn đáp án A.
Câu 14:
 Xem đáp án
Xem đáp án
Ta có: 1 + 3 + 5 + 7 + 9 + … + 19
= 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19
= (1 + 19) + (3 + 17) + (5 + 15) + (7 + 13) + (9 + 11)
= 20 + 20 + 20 + 20 + 20
= 40 + 20 + 20 + 20
= 60 + 20 + 20
= 80 + 20 = 100
Vậy kết quả của tổng 1 + 3 + 5 + 7 + 9 + … + 19 có chữ số tận cùng là 0.
Chọn đáp án D.
Câu 15:
Kết quả của phép tính 25 . 12 . 4 là:
 Xem đáp án
Xem đáp án
Ta có: 25 . 12 . 4 = 25 . 4 . 12 = (25 . 4) . 12 = 100 . 12 = 1 200
Chọn đáp án B.
Câu 16:
 Xem đáp án
Xem đáp án
Phép chia a : b thực hiện được khi số chia b phải khác 0, tức là b ≠ 0.
Chọn đáp án C.
Câu 17:
 Xem đáp án
Xem đáp án
Ta có: 2 021 . (x – 2 021) = 2 021
x – 2 021 = 2 021 : 2 021
x – 2 021 = 1
x = 1 + 2 021
x = 2 022
Vậy x = 2 022.
Chọn đáp án C.
Câu 18:
 Xem đáp án
Xem đáp án
Ta có:
+) 53= 125; 35= 243 suy ra 53< 35
nên A đúng.+) 34= 81; 25= 32 suy ra 34>25nên B đúng.
+) 43= 64; 26= 64 suy ra 43= 26nên C đúng.
+) 43= 64; 82= 64 suy ra 43= 82nên D sai.
Chọn đáp án D.
Câu 19:
 Xem đáp án
Xem đáp án
Ta có: 34= 81 nên 3n= 34, do đó n = 4.
Chọn đáp án C.
Câu 20:
 Xem đáp án
Xem đáp án
Ta có: 43. 45= 43+5= 48nên 4n= 48suy ra n = 8.
Chọn đáp án C.
Câu 21:
Tìm số tự nhiên m thỏa mãn 202018< 20m</>< 202020</>?
 Xem đáp án
Xem đáp án
Ta có: 202018< 20m</>
< 202020</>
Suy ra: 2 018 < m < 2 020
Mà m là số tự nhiên nên m = 2 019.
Vậy m = 2 019.
Chọn đáp án B.
</>
Câu 22:
 Xem đáp án
Xem đáp án
Ta có: 2 . [(195 + 35 : 7) : 8 + 195] – 400
= 2 . [(195 + 5) : 8 + 195] – 400
= 2 . [200 : 8 + 195] – 400
= 2 . [25 + 195] – 400
= 2 . 220 – 400 = 40
Chọn đáp án D.
Câu 23:
 Xem đáp án
Xem đáp án
Ta có: 34. 6 – [131 – (15 – 9)2]
= 34. 6 – [131 – 62]
= 81 . 6 – [131 – 36]
= 81 . 6 – 95
= 486 – 95 = 391
Chọn đáp án D.
Câu 24:
 Xem đáp án
Xem đáp án
Ta có: y ⁝ 4 nên suy ra y ⁝ 2 (vì 4 chia hết cho 2)
Khi đó ta có:
x ⁝ 2 và y ⁝ 2 nên suy ra (x + y) ⁝ 2 (theo tính chất chia hết của một tổng).
Chọn đáp án A.
Câu 25:
 Xem đáp án
Xem đáp án
Trong các số đã cho, ta thấy: 18 : 3 = 6, 75 : 3 = 25, 258 : 3 = 86.
Do đó ta có: 18 ⁝ 3, 75 ⁝ 3, 258 ⁝ 3 nên 18; 75; 258 là các bội của 3.
Vậy ta viết tập hợp A là: A = {18; 75; 258}.
Chọn đáp án D.
Câu 26:
 Xem đáp án
Xem đáp án
Vì 6 ⁝ (x – 2) nên x – 2 là ước của 6.
Mà các ước của 6 là: 1, 2, 3, 6.
Nên ta có các trường hợp sau:
• TH1: x – 2 = 1
Suy ra x = 1 + 2 = 3 (t/m)
• TH2: x – 2 = 2
Suy ra x = 2 + 2 = 4 (t/m)
• TH3: x – 2 = 3
Suy ra x = 3 + 2 = 5 (t/m)
• TH4: x – 2 = 6
Suy ra x = 6 + 2 = 8 (t/m)
Vậy tập hợp các số tự nhiên x thỏa mãn yêu cầu bài toán là: {3; 4; 5; 8}.
Chọn đáp án D.
Câu 27:
 Xem đáp án
Xem đáp án
Vì 5 chia hết cho 5 nên theo tính chất chia hết của một tích ta có
1 . 2 . 3 . 4 . 5 . 6 chia hết cho 5
Lại có 35 có chữ số tận cùng là 5 nên 35 chia hết cho 5
Do đó theo tính chất chia hết của một hiệu ta có
1 . 2 . 3 . 4 . 5 . 6 – 35 chia hết cho 5.
Chọn đáp án D.
Câu 28:
Tìm số thích hợp ở dấu * để số ![]() chia hết cho 9.
chia hết cho 9.
 Xem đáp án
Xem đáp án
Số ![]() có tổng các chữ số là 3 + * + 7 = 10 + *
có tổng các chữ số là 3 + * + 7 = 10 + *
Ta có ![]() chia hết cho 9 thì 10 + * cũng phải chia hết cho 9
chia hết cho 9 thì 10 + * cũng phải chia hết cho 9
Trong các đáp án đã cho, ta thấy chỉ có * = 8 là thỏa mãn (vì 10 + 8 = 18 chia hết cho 9).
Vậy * = 8.
Chọn đáp án C.
Câu 29:
Tìm các số tự nhiên x, y biết rằng 23x5y chia hết cho 2, 5 và 9.
 Xem đáp án
Xem đáp án
Ta có x, y là các chữ số trong số 23x5y nên x, y ∈ {0; 1; 2; 3; 4; 5; 6; 7; 8; 9}
Theo giả thiết ta có 23x5y chia hết cho 2 và 5 nên y = 0, ta được số 23x50
Mà 23x5y nên 2 + 3 + x + 5 chia hết cho 9 hay (10 + x) chia hết cho 9.
Thử các kết quả ta thấy x = 8 thỏa mãn yêu cầu bài.
Vậy x = 8; y = 0.
Chọn đáp án C.
Câu 30:
 Xem đáp án
Xem đáp án
Ta có
+ Đáp án A: 15 – 5 + 3 = 13 là số nguyên tố.
+ Đáp án B: 7 . 2 + 1 = 15 là hợp số.
+ Đáp án C: 14 . 6 : 4 = 84 : 4 = 21 là hợp số.
+ Đáp án D: 6 . 4 – 12 . 2 = 24 – 24 = 0 không phải là số nguyên tố, cũng không phải là hợp số.
Chọn đáp án A.
Câu 31:
 Xem đáp án
Xem đáp án
+ Số 21 có các ước là 1; 3; 7; 21 nên 21 là hợp số.
+ Số 71 chỉ có hai ước là 1; 71 nên 71 là số nguyên tố.
+ Số 77 có các ước là 1; 7; 11; 77 nên 77 là hợp số.
+ Số 101 chỉ có hai ước là 1; 101 nên 101 là số nguyên tố.
Vậy trong các số đã cho, có 2 số là số nguyên tố và hai số là hợp số.
Chọn đáp án B.
Câu 32:
 Xem đáp án
Xem đáp án
Vì 90 ⁝ a nên a là ước của 90
và 135 ⁝ a nên a là ước của 135
Suy ra a là ước chung của 90 và 135.
Vì a là số lớn nhất thỏa mãn điều kiện trên nên a = ƯCLN (90, 135).
Phân tích các số 90 và 135 ra thừa số nguyên tố, ta được:
90 = 2 . 32. 5
135 = 33. 5
Vậy ƯCLN(90, 135) = 32. 5 = 45 hay a = 45.
Chọn đáp án C.
Câu 33:
 Xem đáp án
Xem đáp án
Ta có:
40 = 23. 5
28 = 22. 7
140 = 22. 5 . 7
Do đó: BCNN(40, 28, 140) = 23. 5 . 7 = 280.
Chọn đáp án B.
Câu 34:
 Xem đáp án
Xem đáp án
Gọi x là số học sinh lớp 6A, 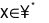 .
.
Vì khi xếp hàng 2, hàng 3, hàng 6, hàng 8 đều vừa đủ hàng nên
x ⁝ 2, x ⁝ 3, x ⁝ 6, x ⁝ 8
Do đó x là bội chung của 2; 3; 6 và 8.
Ta có:
6 = 2 . 3
8 = 23
Do đó: BCNN(2, 3, 6, 8) = 23. 3 = 24
Suy ra BC(2, 3, 6, 8) = B(24) = {0; 24; 48; 72; ...}
Vì 40 < x < 60
Do đó: x = 48.
Chọn đáp án A.
Câu 35:
Trong hai số sau, hai số nào là hai số nguyên tố cùng nhau:
 Xem đáp án
Xem đáp án
Ta có:
ƯC(2, 6) = {1; 2} nên ƯCLN(2, 6) = 2
ƯC(3, 10) = {1} nên ƯCLN(3, 10) = 1
ƯC(6, 9) = {1; 3} nên ƯCLN(6, 9) = 3
ƯC(15, 33) = {1; 3} nên ƯCLN(15, 33) = 3
Chú ý: Hai số gọi là nguyên tố cùng nhau nếu chúng có ước chung lớn nhất là 1.
Vậy 3 và 10 là hai số nguyên tố cùng nhau.
Chọn đáp án B.
