Trắc nghiệm Bài 10: Số nguyên tố. Hợp số có đáp án ( Vận dụng )
-
579 lượt thi
-
5 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
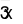là số nguyên tố.
Xem đáp án
Thay lần lượt các đáp án vào để thử.
+ Đáp án A: 37 là số nguyên tố vì nó lớn hơn 1 và chỉ có hai ước là 1 và chính nó.
+ Đáp án B: 34 không phải là số nguyên tố vì 34 chia hết cho 2 nên có thêm ít nhất 1 ước nữa là 2 ngoài 1 và 34.
+ Đáp án C: 36 không phải là số nguyên tố vì 36 chia hết cho 2 nên có thêm ít nhất 1 ước nữa là 2 ngoài 1 và 36.
+ Đáp án D: 39 không phải là số nguyên tố vì 39 chia hết cho 3 nên có thêm ít nhất 1 ước nữa là 2 ngoài 1 và 39.
Chọn đáp án A.
Câu 2:
Xem đáp án
Số tự nhiên có hai chữ số với chữ số hàng đơn vị là 7 là: 17; 27; 37; 47; 57; 67; 77; 87; 97.
Trong đó, số nguyên tố là các số: 17; 37; 47; 67; 97.
Vậy có 5 số thỏa mãn yêu cầu bài toán.
Chọn đáp án A.
Câu 3:
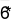là số nguyên tố. Xem đáp án
Đáp án A: Ta được số 65. Vì 65 chia hết cho 5 nên 65 là hợp số
Đáp án B: Ta được số 66. Vì 66 chia hết cho 2 nên 66 là hợp số
Đáp án C: Ta được số 67. Vì 67 chỉ có 2 ước là 1 và chính nó nên 67 là số nguyên tố
Đáp án D: Ta được số 68. Vì 68 chia hết cho 2 nên 68 là hợp số.
Chọn đáp án C.
Câu 4:
Xem đáp án
Các số nguyên tố nhỏ hơn hoặc bằng 5 là: 2; 3; 5.
Vì số cần tìm là số tự nhiên có hai chữ số khác nhau, chia hết cho cả 2 và 5 nên có dạng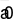 
với 
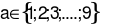. Vì 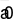chia hết cho 3 nên tổng các chữ số của nó là a + 0 = a chia hết cho 3 nên a ∈ {3; 6; 9}.
Vì 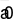là số nhỏ nhất nên a = 3
Vậy số cần tìm là 30.
Chọn đáp án C.
Câu 5:
Xem đáp án
Ta có:
A = 11 . 12 . 13 + 14 . 15
Vì 12 chia hết cho 2 nên 11 . 12 . 13 chia hết cho 2
Vì 14 chia hết cho 2 nên 14 . 15 chia hết cho 2
Do đó tổng 11 . 12 . 13 + 14 . 15 chia hết cho 2 hay A chia hết cho 2
Hiển nhiên A >1
Vậy A hợp số.
B = 11 . 13. 15 + 17 . 19 . 23
Vì 11 . 13 . 15 là tích của 3 số lẻ nên nó là một số lẻ
Tương tự tích 17 . 19 . 23 cũng là một số lẻ
Do đó 11 . 13. 15 + 17 . 19 . 23 là tổng của hai số lẻ nên 11 . 13. 15 + 17 . 19 . 23 phải là số chẵn và lớn hơn 2 nên 11 . 13. 15 + 17 . 19 . 23 là hợp số, hay B là hợp số.
Vậy cả A và B đều là hợp số.
Chọn đáp án B.