Trắc nghiệm Các dạng toán về phân số với tử số và mẫu số là số nguyên (có đáp án)
Trắc nghiệm Các dạng toán về phân số với tử số và mẫu số là số nguyên (có đáp án)
-
669 lượt thi
-
14 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Xem đáp án
+) \[\frac{{12}}{0}\] không là phân số vì mẫu số bằng 0.
+) \[\frac{3}{{0,25}}\] không là phân số vì mẫu số là số thập phân.
+) \[\frac{{4,4}}{{11,5}}\] không là phân số vì tử số và mẫu số là số thập phân.
+) \[\frac{{ - 4}}{5}\]là phân số vì −4; 5∈Z và mẫu số là 5 khác 0.
Đáp án cần chọn là: B
Câu 2:
Xem đáp án
Trong hình có 2 ô vuông tô màu và tổng tất cả 8 ô vuông nên phân số biểu thị là \[\frac{2}{8} = \frac{1}{4}\]
Đáp án cần chọn là: B
Câu 3:
Xem đáp án
\[\frac{{35}}{{15}} = \frac{x}{3}\]
35 . 3 = 15 . x
\[x = \frac{{35.3}}{{15}}\]
x = 7
Vậy x = 7
Đáp án cần chọn là: A
Câu 4:
Xem đáp án
Các phân số thỏa mãn bài toán là:
\[\frac{1}{{ - 2}};\frac{3}{{ - 2}};\frac{4}{{ - 2}};\frac{{ - 2}}{1};\frac{{ - 2}}{3};\frac{{ - 2}}{4}\]
Vậy có tất cả 6 phân số.
Đáp án cần chọn là: B
Câu 5:
Xem đáp án
Vì C∈N nên C∈Z. Do đó ta tìm n∈Z để C∈Z
Vì n∈Z nên để C∈Z thì 2n+1∈U(11) = {±1; ±11}
Ta có bảng:
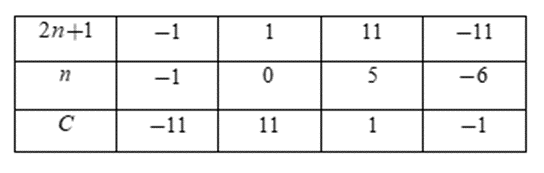
Vì C∈N nên ta chỉ nhận các giá trị n = 0; n = 5
Đáp án cần chọn là: C
Câu 6:
Xem đáp án
Vì n nguyên dương nên để \[\frac{9}{{4n + 1}}\]nguyên thì 4n+1∈U(9) = {±1; ±3; ±9}
Ta có bảng:
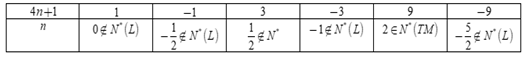
Vậy có duy nhất một giá trị của n thỏa mãn là n = 2
Đáp án cần chọn là: A
Câu 7:
Xem đáp án
Ta có:
\[\frac{6}{9} = \frac{{12}}{a} \Rightarrow 6.a = 9.12 \Rightarrow a = \frac{{9.12}}{6} = 18\]
\[\frac{6}{9} = \frac{b}{{ - 54}} \Rightarrow 6.\left( { - 54} \right) = 9.b \Rightarrow b = \frac{{6.\left( { - 54} \right)}}{9} = - 36\]
\[\frac{6}{9} = \frac{{ - 738}}{c} \Rightarrow 6.c = 9.\left( { - 738} \right) \Rightarrow c = \frac{{9.\left( { - 738} \right)}}{6} = - 1107\]
Vậy a + b + c = 18 + (-36) + (-1107) = - 1125
Đáp án cần chọn là: B
Câu 8:
Xem đáp án
- Các phân số dương: \[\frac{{15}}{{60}};\frac{6}{{15}};\frac{3}{{12}}\]
+ Vì 15.15 ≠ 60.6 nên \[\frac{{15}}{{60}} \ne \frac{6}{{15}}\]
+ Vì 6.12 ≠ 15.3 nên \[\frac{6}{{15}} \ne \frac{3}{{12}}\]
+ Vì 15.12 = 60.3 nên \[\frac{{15}}{{60}} = \frac{3}{{12}}\]
- Các phân số âm: \[\frac{{ - 7}}{5};\frac{{28}}{{ - 20}}\]
Vì (−7).(−20) = 5.28 nên \[\frac{{ - 7}}{5};\frac{{28}}{{ - 20}}\]
Vậy có hai cặp phân số bằng nhau trong các phân số đã cho.
Đáp án cần chọn là: D
Câu 9:
Xem đáp án
Ta có:
\[A = \frac{{3n - 5}}{{n + 4}}\]
\[ = \frac{{3n + 12 - 12 - 5}}{{n + 4}}\]
\[ = \frac{{3\left( {n + 4} \right) + \left( { - 17} \right)}}{{n + 4}}\]
\[ = \frac{{3\left( {n + 4} \right)}}{{n + 4}} + \frac{{ - 17}}{{n + 4}}\]
\[ = 3 + \frac{{ - 17}}{{n + 4}}\]
Vì n∈Z nên để A∈Z thì n+4∈U(−17) = {±1; ±17}
Ta có bảng:
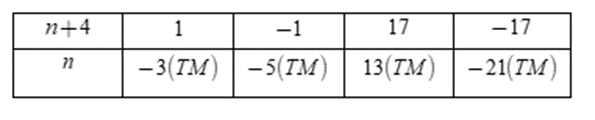
Vậy n∈{−21; −5; −3; 13}
Đáp án cần chọn là: B
Câu 10:
Xem đáp án
Ta có:
\[\frac{x}{5} = \frac{3}{y}\]⇒ x.y = 5.3 = 15
Mà 15 = 5.3 = 15.1 = (−3).(−5) = (−1).(−15)
và x,y ∈ Z, x >y nên (x;y) ∈ {(5;3), (15;1), (−3;−5), (−1;−15)}
Đáp án cần chọn là: A
Câu 11:
Xem đáp án
Ta có: x – y = 5 ⇒ x = y + 5 thay vào \[\frac{{x - 4}}{{y - 3}} = \frac{4}{3}\]ta được:
\[\frac{{y + 5 - 4}}{{y - 3}} = \frac{4}{3}\]
\[\frac{{y + 1}}{{y - 3}} = \frac{4}{3}\]
3(y + 1) = 4(y − 3)
3y + 3 = 4y − 12
3y − 4y = −12 − 3
−y = −15
y = 15
⇒ x = 15 + 5 = 20
Vậy x = 20; y = 15
Đáp án cần chọn là: C
Câu 12:
Xem đáp án
\[\frac{x}{3} = \frac{{27}}{x}\]
x.x = 81
x2 = 81
Ta có: x = 9 hoặc x = −9
Kết hợp điều kiện x < 0 nên có một giá trị x thỏa mãn là: x = −9
Đáp án cần chọn là: C
Câu 13:
Xem đáp án
Viết số nguyên −16 dưới dạng phân số ta được: \[\frac{{ - 16}}{1}\]
Đáp án cần chọn là: C
Câu 14:
Xem đáp án
Phân số \[\frac{{ - 9}}{7}\]được đọc là: Âm chín phần bảy
Đáp án cần chọn là: D