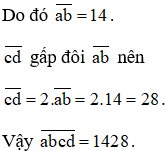Bài 5: Phép cộng và phép nhân
-
684 lượt thi
-
28 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Điền vào chỗ trống:
| a | 12 | 21 | 1 | |
| b | 5 | 0 | 48 | 15 |
| a + b | ||||
| a . b | 0 | |||
| (1) | (2) | (3) | (4) |
 Xem đáp án
Xem đáp án
- Ở cột (1) ta có a = 12, b = 5 nên a + b = 12+ 5 = 17 và a . b = 12.5 = 60
- Ở cột (2) ta có a = 21, b = 0 nên a + b = 21 + 0 = 21 và a . b = 21.0 = 0
- Ở cột (3) ta có a = 1, b = 48 nên a + b = 1 + 48 = 49 và a . b = 1.48 = 48
- Ở cột (4) ta có b = 15, a . b = 0 nên a = 0: 15 = 0 và a + b = 0 + 15 = 15
Ta có bảng:
| a | 12 | 21 | 1 | 0 | |
| b | 5 | 0 | 48 | 15 | |
| a + b | 17 | 21 | 49 | 15 | |
| a . b | 60 | 0 | 48 | 0 |
Câu 2:
Điền vào chỗ trống: Tích của một số với 0 thì bằng …
 Xem đáp án
Xem đáp án
Tích của một số với 0 thì bằng 0.
Câu 3:
Điền vào chỗ trống: Nếu tích của hai thừa số mà bằng 0 thì có ít nhất một thừa số bằng …
 Xem đáp án
Xem đáp án
Nếu tích của hai thừa số mà bằng 0 thì có ít nhất một thừa số bằng 0.
Câu 6:
Tính nhanh: 87.36 + 87.64;
 Xem đáp án
Xem đáp án
Ta có:
87 . 36 + 87 . 64 = 87 . ( 36 + 64 ) = 87 . 100 = 8700
Câu 7:
Cho các số liệu về quãng đường bộ:
Hà Nội – Vĩnh Yên : 54km
Vĩnh Yên – Việt Trì : 19km
Việt Trì – Yên Bái : 82km
Tính quãng đường một ô tô đi từ Hà Nội lên Yên Bái qua Vĩnh Yên và Việt Trì.
 Xem đáp án
Xem đáp án
Ô tô đi từ Hà Nội lên Yên Bái và đi qua Vĩnh Yên, Việt Trì nên ta có: :
(HN – YB) = (HN – VY) + (VY – VT) + (VT – YB)
= 54 + 19 + 82 = 73 + 82 = 155 (km)
(Trong đó: (HN – YB) là quãng đường Hà Nội – Yên Bái) :
(HN – VY) là quãng đường Hà Nội – Vĩnh Yên. :
(VY – VT) là quãng đường Vĩnh Yên – Việt Trì :
(VT – YB) là quãng đường Việt Trì – Yên Bái).
Câu 8:
Áp dụng các tính chất của phép cộng và phép nhân để tính nhanh: 86 + 357 + 14
 Xem đáp án
Xem đáp án
86 +357 + 14 = (86 +14) + 357 = 100 + 357 = 457
Câu 9:
Áp dụng các tính chất của phép cộng và phép nhân để tính nhanh: 72 + 69 + 128
 Xem đáp án
Xem đáp án
72 + 69 + 128 = (72 +128) + 69 = 200 + 69 = 269
Câu 10:
Áp dụng các tính chất của phép cộng và phép nhân để tính nhanh: 25.5.4.27.2
 Xem đáp án
Xem đáp án
25.5.4.27.2 = (25.4).(5.2).27 = 100.10.27 = 27000
Câu 11:
Áp dụng các tính chất của phép cộng và phép nhân để tính nhanh: 28.64 + 28.36
 Xem đáp án
Xem đáp án
28.64 + 28.36 = 28.(64+36) =28.100 =2800.
Câu 12:
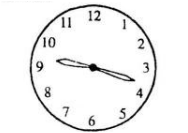
Trên hình 12, đồng hồ chỉ 9 giờ 18 phút, hai kim đồng hồ chia mặt đồng hồ thành hai phần, mỗi phần có sáu số. Tính tổng các số ở mỗi phần, em có nhận xét gì?
Hình 12
 Xem đáp án
Xem đáp án
Các số ở nửa mặt trên đồng hồ gồm: 10, 11, 12, 1, 2, 3. Tổng của chúng bằng:
10 + 11 + 12 + 1 + 2 + 3 = (10 + 3) + (11 + 2) + (12 + 1) = 13 + 13 + 13 = 3.13 = 39.
Các số ở nửa mặt dưới đồng hồ gồm: 4, 5, 6, 7, 8, 9. Tổng của chúng bằng:
4 + 5 + 6 + 7 + 8 + 9 = (4+9) + (5+8) + (6+7) = 13 + 13 + 13 = 3.13 = 39.
Nhận xét: Khi cộng một dãy số gồm nhiều số, ta có thể nhóm các số thành cách nhóm thích hợp để thuận lợi cho việc tính toán.
Câu 13:
Điền vào chỗ trống trong bảng thanh toán sau:
| Số thứ tự | Loại hàng | Số lượng (quyển) | Giá đơn vị (đồng) | Tổng số tiền (đồng) |
| 1 | Vở loại 1 | 35 | 2000 | ... |
| 2 | Vở loại 2 | 42 | 1500 | ... |
| 3 | Vở loại 3 | 38 | 1200 | ... |
| Cộng: | ... | |||
 Xem đáp án
Xem đáp án
| Số thứ tự | Loại hàng | Số lượng (quyển) | Giá đơn vị (đồng) | Tổng số tiền (đồng) |
| 1 | Vở loại 1 | 35 | 2000 | 70000 |
| 2 | Vở loại 2 | 42 | 1500 | 63000 |
| 3 | Vở loại 3 | 38 | 1200 | 45600 |
| Cộng: | 178600 | |||
Số tiền vở loại 1 là 35.2000 = 70 000 (đồng)
Điển vào chỗ trống dòng thứ nhất 70 000
Số tiền vở loại 2 là 42.1500 = 63 000 (đồng)
Điền vào chỗ trống dòng thứ hai 63 000
Số tiền vở loại 3 là 38.1200 = 45 000 (đồng)
Điền vào chỗ trống dòng thứ ba 45 600
Tổng số tiền cần trả là: 70 000 + 63 000 + 45 600 = 178 600 (đồng)
Điền vào chỗ trống dòng thứ tư là 178 600.
Câu 14:
Tìm số tự nhiên x, biết: (x - 34).15 = 0
 Xem đáp án
Xem đáp án
Một tích bằng 0 chỉ khi có ít nhất một thừa số bằng 0.
(x – 34).15 = 0
x – 34 = 0 (vì 15 > 0)
x = 34.
Câu 15:
Tìm số tự nhiên x, biết: 18.(x - 16) = 18
 Xem đáp án
Xem đáp án
18.(x – 16) = 18
x – 16 = 18 : 18
x – 16 = 1
x = 1 + 16
x = 17.
Câu 16:
Tính nhanh: 135 + 360 + 65 + 40
 Xem đáp án
Xem đáp án
135 + 360 + 65 + 40 = (135+65) + (360+40) = 200 + 400 = 600;
Câu 17:
Tính nhanh: 463 + 318 + 137 + 22
 Xem đáp án
Xem đáp án
463 + 318 + 137 + 22 = (463 + 137) + (318 +22) = 600 + 340 = 940
Câu 18:
Tính nhanh: 20 + 21 + 22 + ... + 29 + 30
 Xem đáp án
Xem đáp án
20 + 21 + 22 + …..+ 29 + 30
= (20 + 30) + (21 + 29) + (22 + 28) + (23 + 27) + (24 + 26) + 25
= 50 + 50 + 50 + 50 + 50 + 25
= 5.50 + 25 = 250 + 25 = 275
Câu 19:
Có thể tính nhanh tổng 97 + 19 bằng cách áp dụng tính chất kết hợp của phép cộng:
97 + 19 = (97 + 3) + 16 = 100 + 16 = 116
Hãy tính nhanh các tổng sau bằng cách làm tương tự như trên: 996 + 45
 Xem đáp án
Xem đáp án
996 + 45 = 996 + (4 + 41) = (996 + 4) + 41 = 1000 + 41 = 1041
Câu 20:
Có thể tính nhanh tổng 97 + 19 bằng cách áp dụng tính chất kết hợp của phép cộng:
97 + 19 = (97 + 3) + 16 = 100 + 16 = 116
Hãy tính nhanh các tổng sau bằng cách làm tương tự như trên: 37 + 198
 Xem đáp án
Xem đáp án
37 + 198 = (35 + 2) + 198 = (198 + 2) + 35 = 200 + 35 = 235
Câu 21:
Cho dãy số sau 1, 1, 2, 3, 5, 8, ...
Trong dãy số trên mỗi số (kể từ số thứ ba) bằng tổng của hai số liền trước. Hãy viết tiếp bốn số nữa vào dãy số.
 Xem đáp án
Xem đáp án
Trong dãy số 1, 1, 2, 3, 5, 8 ….. ta có:
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
3 + 5 = 8
Theo quy luật như trên, các số tiếp theo của dãy là:
5 + 8 = 13
8 + 13 = 21
13 + 21 = 34
21 + 34 = 55.
Câu 22:
Tìm các tích bằng nhau mà không cần tính kết quả của mỗi tích.
15.2.6; 4.4.9; 5.3.12; 8.18; 15.3.4; 8.2.9
 Xem đáp án
Xem đáp án
Ta có :
15.2.6 = 15.(2.6) = 15.12
5.3.12 = (5.3).12 = 15.12
15.3.4 = 15.(3.4) = 15.12
4.4.9 = 4.(2.2).9 = (4.2).(2.9) = 8.18
8.2.9 = 8.(2.9) = 8.18
Do đó ta có các tích bằng nhau là :
15.2.6 = 5.3.12 = 15.3.4
4.4.9 = 8.18 = 8.2.9
Câu 23:
Có thể tính nhẩm tích 45.6 bằng cách:
Áp dụng tính chất kết hợp của phép nhân:
45.6 = 45.(2.3) = (45.2).3 = 90 .3 = 270
Áp dụng tính chất phân phối của phép nhân đối với phép cộng:
45.6 = (40+ 5).6 = 40.6 + 5.6 = 240 +30 = 270
Hãy tính nhẩm bằng cách áp dụng tính chất kết hợp của phép nhân:
15.4; 25.12; 125.16
 Xem đáp án
Xem đáp án
Áp dụng tính chất kết hợp của phép nhân a.b.c = a.(b.c) =(a.b).c ta có:
15.4 = (3.5).4 = 3.(5.4) = 20.3 = 60 hoặc 15.4 = 15.(2.2) = (15.2).2 = 30.2 = 60.
25.12 = 25.(4.3) = (25.4).3 = 100.3 = 300.
125.16 = 125.(8.2) = (125.8).2 = 1000.2 = 2000
Câu 24:
Có thể tính nhẩm tích 45.6 bằng cách:
Áp dụng tính chất kết hợp của phép nhân:
45.6 = 45.(2.3) = (45.2).3 = 90 .3 = 270
Áp dụng tính chất phân phối của phép nhân đối với phép cộng:
45.6 = (40+ 5).6 = 40.6 + 5.6 = 240 +30 = 270
Hãy tính nhẩm bằng cách áp dụng tính chất phân phối của phép nhân đối với phép cộng:
25.12; 34.11; 47.101
 Xem đáp án
Xem đáp án
Áp dụng tính chất phân phối của phép nhân đối với phép cộng: a(b+c)=ab+ac ta có:
25.12 = 25.(10 + 2) = 25.10 + 25.2 = 250 + 50 = 300.
34.11 = 34.(10 + 1) = 34.10 + 34 = 340 + 34 = 374.
47.101 = 47.(100 + 1) = 47.100 + 47.1 = 4700 + 47 = 4747.
Câu 25:
Áp dụng tính chất a.(b - c) = a.b – a.c để tính nhẩm. Ví dụ:
13.99 = 13.(100 - 1) = 13.100 - 13.1 = 1300 - 13 = 1287
Hãy tính: 16.19; 46.99; 35.98
 Xem đáp án
Xem đáp án
Ta tách các số 19, 99, 98 thành các hiệu, trong đó có chứa số tròn chục hoặc tròn trăm rồi áp dụng tính chất: a(b – c) = ab – ac để tính nhanh như sau:
16.19 = 16.(20 – 1) = 16.20 – 16 = 320 – 16 = 304;
46.99 = 46.(100 – 1) = 46.100 – 46 = 4600 – 46 = 4554;
35.98 = 35.(100 – 2) = 35.100 – 35.2 = 3500 – 70 = 3430.
Câu 26:
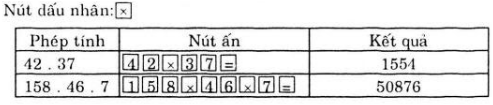
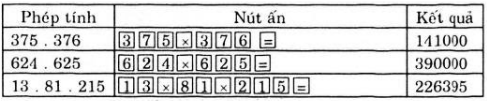
Sử dụng máy tính bỏ túi:
Dùng máy tính bỏ túi để tính:
375.376; 624.625; 13.81.215
 Xem đáp án
Xem đáp án
Kết quả:
375.376 = 141000
624.625 = 390000
13.81.215 = 226395
Cách bấm nút:
Câu 27:
Đố. Số 142857 có tính chất rất đặc biệt. Hãy nhân nó với mỗi số 2, 3, 4, 5, 6 em sẽ tìm được tính chất đăc biệt ấy
 Xem đáp án
Xem đáp án
142857 x 2 = 285714
142857 x 3 = 428571
142857 x 4 = 571428
142857 x 5 = 714285
142857 x 6 = 857142
* Nhận xét: Các tích trên được viết bởi các chữ số 2,8, 5, 7, 1, 4
Nếu ta sắp xếp lại các kết quả trên theo thứ tự 142857; 428571; 285714; 857142; 57142; 714285
Thì được một dãy mà mỗi số hạng sau thu được bằng cách chuyển chữ số đứng đầu, bên trái thành chữ số cuối.
Câu 28:
Bình Ngô đại cáo ra đời năm nào?
Năm 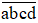
 Xem đáp án
Xem đáp án
- Ta biết rằng mỗi tuần có bảy ngày nên số ngày trong hai tuần là 7.2 = 14 (ngày). Do đó:
Vậy Nguyễn trãi viết Bình Ngô đại cáo vào năm 1428.