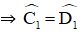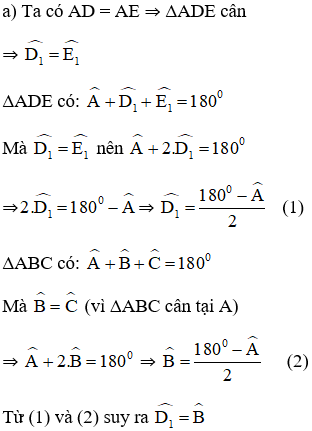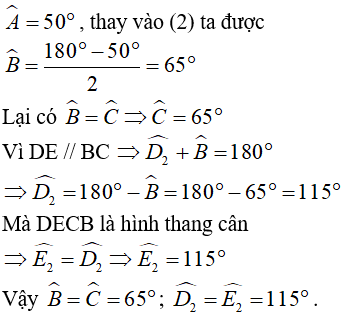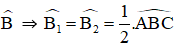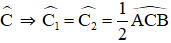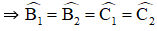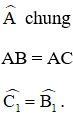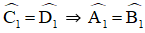Bài 3: Hình thang cân
-
4389 lượt thi
-
12 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
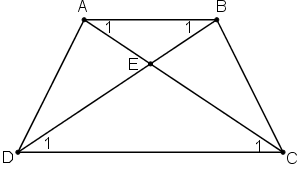
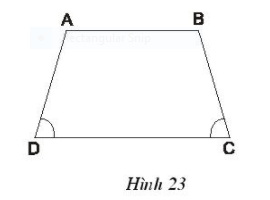
Hình thang ABCD (AB // CD) trên hình 23 có gì đặc biệt ?
Xem đáp án
Hình thang ABCD trên hình 23 có hai góc kề cạnh đáy lớn bằng nhau
Câu 2:
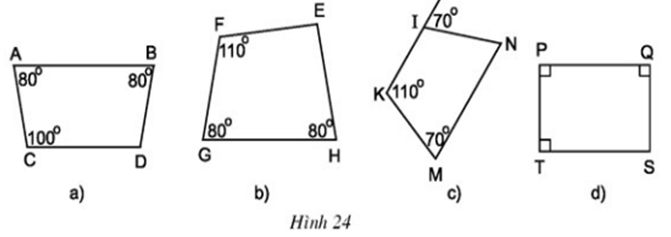
Cho hình 24.
a) Tìm các hình thang cân.
b) Tính các góc còn lại của mỗi hình thang cân đó.
c) Có nhận xét gì về hai góc đối của hình thang cân ?
Xem đáp án
a) Các hình thang cân là : ABDC, IKMN, PQST
b) Áp dụng định lí tổng các góc của một tứ giác bằng 3600
⇒ góc D = 360o- 80o- 80o- 100o = 100o
Góc N = 70o(so le trong với góc 70o)
Góc S = 360o- 90o- 90o- 90o = 90o
c) Hai góc đối của hình thang cân bù nhau
Câu 3:
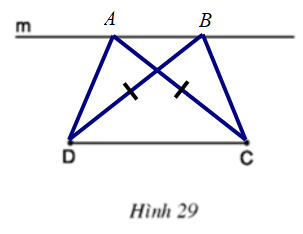
Cho đoạn thẳng CD và đường thẳng m song song với CD (h.29). Hãy vẽ các điểm A, B thuộc m sao cho ABCD là hình thang có hai đường chéo CA, DB bằng nhau. Sau đó hãy đo các góc C ̂ và D ̂ của hình thang ABCD đó để dự đoán về dạng của các hình thang có đường chéo bằng nhau.
Xem đáp án
Hai góc C và D bằng nhau
⇒ Hình thang có hai đường chéo bằng nhau là hình thang cân
Câu 4:
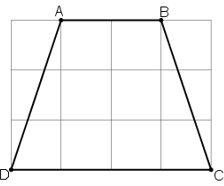
Tính độ dài các cạnh của hình thang cân ABCD trên giấy kẻ ô vuông (h.30, độ dài của cạnh ô vuông là 1cm).
Xem đáp án
(Mỗi ô vuông là 1cm).
Nhìn vào hình vẽ ta thấy :
+ AB = 2cm
+ CD = 4cm.
+ Tính AD :
Xét tam giác vuông ADE có AE = 1cm, DE = 3cm.
⇒ AD2 = AE2 + DE2 (Định lý Pytago)
= 12 + 32 = 10
⇒ AD = √10 cm
+ Tính BC :
ABCD là hình thang cân nên BC = AD = √10 cm.
Vậy AB = 2cm, CD = 4cm, AD = BC = √10 cm.
Kiến thức áp dụng
+ Định lý Pytago: Tam giác ABC vuông tại A ⇔ AB2 + AC2 = BC2.
+ Trong hình thang cân, hai cạnh bên bằng nhau.
Câu 5:
Cho hình thang cân ABCD (AB // CD, AB < CD). Kẻ các đường cao AE, BF của hình thang. Chứng minh rằng DE = CF.
Xem đáp án
Vì hình thang ABCD cân
AD = BC;
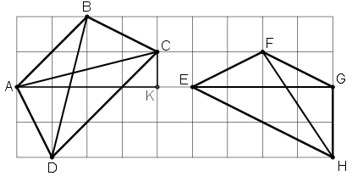
Ĉ = D̂
Xét hai tam giác vuông AED và BFC có:
AD = BC
Ĉ = D̂
⇒ ΔAED = ΔBFC (cạnh huyền – góc nhọn)
⇒ DE = CF.
Kiến thức áp dụng
Trong hình thang cân:
+ Hai góc ở đáy bằng nhau
+ Hai cạnh bên bằng nhau.
Câu 6:
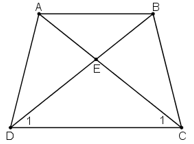
Cho hình thang cân ABCD (AB//CD), E là giao điểm của hai đường chéo. Chứng minh rằng EA = EB, EC = ED.
Xem đáp án
Do ABCD là hình thang cân nên:
AD = BC;
AC = BD;
Xét hai tam giác ADC và BCD, ta có:
AD = BC (gt)
AC = BD (gt)
DC cạnh chung
⇒ ΔADC = ΔBCD (c.c.c)
⇒ ΔECD cân tại E
⇒ EC = ED.
Mà AC = BD
⇒ AC – EC = BD – ED
hay EA = EB.
Vậy EA = EB, EC = ED.
Kiến thức áp dụng
Trong một hình thang cân:
+ Hai đường chéo bằng nhau
+ Hai cạnh bên bằng nhau.
Câu 7:
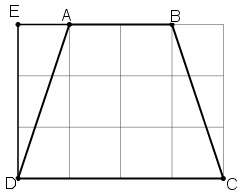
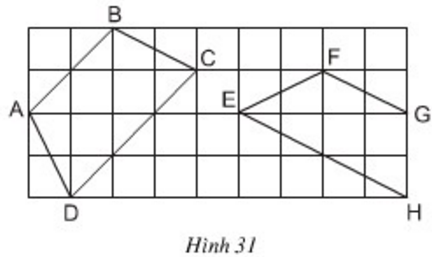
Đố. Trong các tứ giác ABCD, EFGH trên giấy kẻ ô vuông (h.31), tứ giác nào là hình thang cân? Vì sao?
Xem đáp án
+ Xét tứ giác ABCD
Nhận thấy AB // CD ⇒ Tứ giác ABCD là hình thang.
Xét ΔACK vuông tại K ta có: AC2 = AK2 + KC2 = 42 + 12 = 17
Tương tự ta có BD2 = 42 + 12 = 17
⇒ AC2 = BD2
⇒ AC = BD
Vậy hình thang ABCD có hai đường chéo AC = BD nên là hình thang cân.
+ Xét tứ giác EFGH
FG // EH ⇒ Tứ giác EFGH là hình thang.
Lại có : EG = 4cm
FH2 = 22 + 32 = 13 ⇒ FH = √13 ≠ EG.
Vậy hình thang EFGH có hai đường chéo không bằng nhau nên không phải hình thang cân.
Kiến thức áp dụng
+ Để chứng minh một hình thang là hình thang cân, ta sử dụng một trong các cách sau:
- Chứng minh hai góc kề một đáy bằng nhau
- Chứng minh hai đường chéo bằng nhau
+ Định lý Pytago: ΔABC vuông tại A ta luôn có: AB2 + AC2 = BC2.
Câu 8:
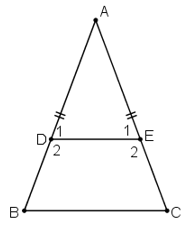
Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy theo thứ tự các điểm D, E sao cho AD = AE
a) Chứng minh rằng BDEC là hình thang cân.
b) Tính các góc của hình thang cân đó, biết rằng góc A = 50o.
Xem đáp án
Mà hai góc ở vị trí đồng vị ⇒ DE // BC
⇒ Tứ giác DECB là hình thang.
Mà hai góc ở đáy B và C bằng nhau nên hình thang DECB là hình thang cân.
b)
Kiến thức áp dụng
+ Tính chất: Trong một hình thang cân, hai góc kề một đáy bằng nhau.
+ Để chứng minh một hình thang là hình thang cân, ta sử dụng một trong các cách sau:
- Chứng minh hai góc kề một đáy bằng nhau.
- Chứng minh hai đường chéo bằng nhau.
Câu 9:
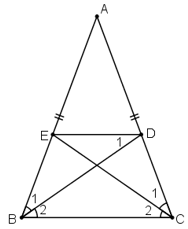
Cho tam giác ABC cân tại A, các đường phân giác BD, CE (D ∈ AC, E ∈ AB). Chứng minh rằng BEDC là hình thang cân có đáy nhỏ bằng cạnh bên.
Xem đáp án
- Chứng minh tứ giác BCDE là hình thang cân:
+ ΔABC cân tại A 
BD là phân giác của 
CE là phân giác của 
+ Xét ΔAEC và ΔADB có:
⇒ ΔAEC = ΔADB
⇒ AE = AD
Vậy tam giác ABC cân tại A có AE = AD
Theo kết quả bài 15a) suy ra BCDE là hình thang cân.
- Chứng minh ED = EB.
ED // BC ⇒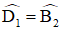 
(Hai góc so le trong)
Mà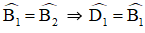 
⇒ ΔEDB cân tại E ⇒ ED = EB.
Vậy ta có EBCD là hình thang cân có đáy nhỏ bằng cạnh bên.
Kiến thức áp dụng
+ Tính chất: Trong một hình thang cân, hai góc kề một đáy bằng nhau.
+ Để chứng minh một hình thang là hình thang cân, ta sử dụng một trong các cách sau:
- Chứng minh hai góc kề một đáy bằng nhau.
- Chứng minh hai đường chéo bằng nhau.
Câu 10:
Hình thang ABCD (AB // CD) có
Chứng minh rằng ABCD là hình thang cân.
Xem đáp án
Gọi E là giao điểm của AC và BD.
+ 
⇒ ΔEDC cân tại E ⇒ ED = EC (1)
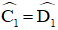
+ AB//CD ⇒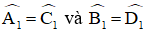 
(Các cặp góc so le trong)
Mà 
⇒ ΔEAB cân tại E ⇒ EA = EB (2)
Từ (1) và (2) suy ra: EA + EC = EB + ED hay AC = BD.
Vậy hình thang ABCD có hai đường chéo AC = BD nên là hình thang cân.
Kiến thức áp dụng
Để chứng minh một hình thang là hình thang cân, ta sử dụng một trong các cách sau:
- Chứng minh hai góc kề một đáy bằng nhau.
- Chứng minh hai đường chéo bằng nhau.
Câu 11:
Chứng minh định lý: "Hình thang có hai đường chéo bằng nhau là hình thang cân" qua bài toán sau: Cho hình thang ABCD (AB // CD) có AC = BD. Qua B kẻ đường thẳng song song với AC, cắt đường thẳng DC tại tại E. Chứng minh rằng:
a) ΔBDE là tam giác cân.
b) ΔACD = ΔBDC
c) Hình thang ABCD là hình thang cân.
Xem đáp án
a) Hình thang ABEC (AB//CE) có hai cạnh bên AC, BE song song nên chúng bằng nhau: AC = BE (1)
Theo giả thiết AC = BD (2)
Từ (1) và (2) suy ra BE = BD do đó ΔBDE cân
Vậy hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.
Kiến thức áp dụng
+ Nếu một hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau, hai cạnh đáy bằng nhau.
+ Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
Câu 12:
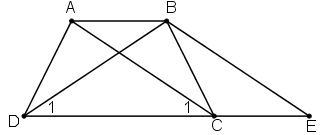
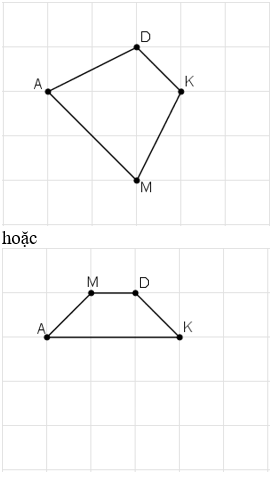
Đố. Cho ba điểm A, D, K trên giấy kẻ ô vuông (h.32) Hãy tìm điểm thứ tư M giao điểm của các dòng kẻ sao cho nó cùng với ba diểm đã cho là bốn đỉnh của một hình thang cân.
Xem đáp án
Ta có thể xác định hai điểm M thỏa mãn như dưới hình.
