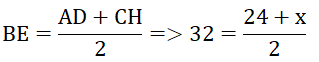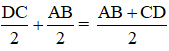Bài 4: Đường trung bình của tam giác, của hình thang
-
4388 lượt thi
-
14 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
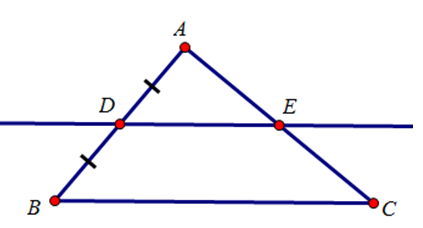
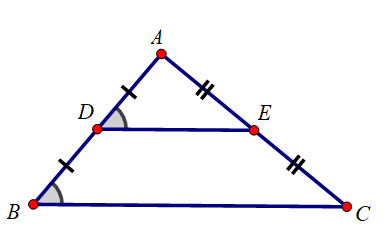
Vẽ tam giác ABC bất kì rồi lấy trung điểm D của AB. Qua D vẽ đường thẳng song song với BC, đường thẳng này cắt AC ở E. Bằng quan sát, hãy nêu dự đoán về vị trí của điểm E trên cạnh AC.
 Xem đáp án
Xem đáp án
Dự đoán: E là trung điểm cạnh AC
Câu 4:
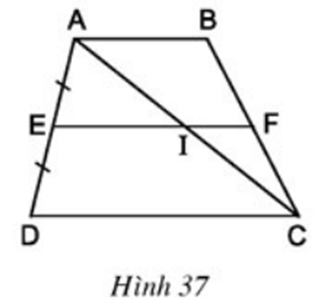
Cho hình thang ABCD (AB // CD). Qua trung điểm E của AD kẻ đường thẳng song song với hai đáy, đường thẳng này cắt AC ở I, cắt BC ở F (h.37). Có nhận xét gì về vị trí của điểm I trên AC, điểm F trên BC ?
 Xem đáp án
Xem đáp án
Áp dụng định lí 1 đường trung bình của tam giác
ΔADC có E là trung điểm AD và EI song song với cạnh DC
⇒ Điểm I là trung điểm AC
ΔABC có I là trung điểm AC và FI song song với cạnh AB
⇒ điểm F là trung điểm BC
Câu 5:
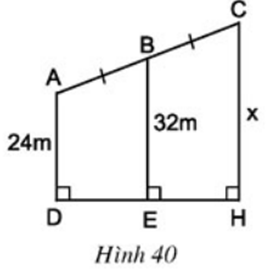
Tính x trên hình 40.
 Xem đáp án
Xem đáp án
Dựa vào hình vẽ ta thấy rằng AD ⊥ DH, CH ⊥ DH, BE ⊥ DH
Suy ra, AD // BE // CH do đó ADHC là hình thang.
Ta thấy rằng, B là trung điểm của AC và BE // AD // CH
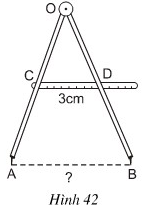
Suy ra BE là đường trung bình của hình thang ADHC, ta có:
⇒ 64 = 24 + x ⇒ x = 40
Câu 6:
Tính x trên hình 41.
 Xem đáp án
Xem đáp án
+ K̂ = Ĉ (= 50º)
⇒ IK // BC (Vì có hai góc đồng vị bằng nhau)
+ KA = KC (= 8cm) nên K là trung điểm AC
Đường thẳng IK đi qua trung điểm cạnh AC và song song với cạnh BC nên đi qua trung điểm cạnh AB
⇒ I là trung điểm AB
⇒ IA = IB hay x = 10cm.
Kiến thức áp dụng
+ Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.
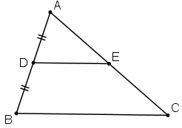
ΔABC, AD = DB , DE // BC ⇒ AE = EC.
Câu 7:
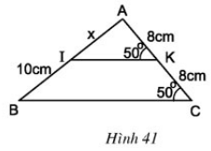
Tính khoảng cách AB giữa hai mũi của compa trên hình 42, biết rằng C là trung điểm của OA, D là trung điểm của OB và CD = 3cm.
 Xem đáp án
Xem đáp án
Ta có: CO = CA (gt)
DO = DB (gt)
⇒ CD là đường trung bình của ΔOAB
⇒ AB = 2CD = 2.3 = 6cm.
Kiến thức áp dụng
+ Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác
+ Đường trung bình của tam giác song song với cạnh thứ ba và bằng một nửa cạnh đó.
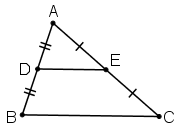
ΔABC, AD = DB, AE = EC ⇒ DE // BC và DE = BC/2.
Câu 8:
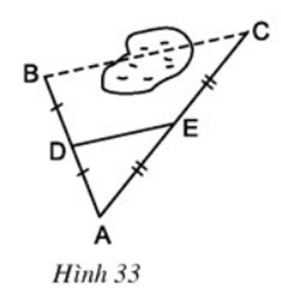
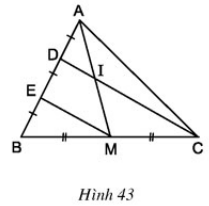
Cho hình 43. Chứng minh rằng AI = IM.
 Xem đáp án
Xem đáp án
ΔBDC có BE = ED và BM = MC
⇒ EM là đường trung bình của ΔBDC
⇒ EM // DC hay EM // DI.
ΔAEM có DI // EM (cmt) và AD = DE (gt)
⇒ IA = IM (Theo định lý 1)
Kiến thức áp dụng
+ Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.

ΔABC, AD = DB , DE // BC ⇒ AE = EC.
+ Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác
+ Đường trung bình của tam giác song song với cạnh thứ ba và bằng một nửa cạnh đó.

ΔABC, AD = DB, AE = EC ⇒ DE // BC và DE = BC/2.
Câu 9:
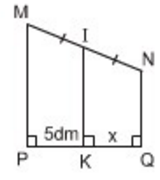
Tìm x trên hình 44.
 Xem đáp án
Xem đáp án
* Ba đường thẳng MP, NQ và IK cùng vuông góc với PQ
=> MP// IK// NQ
=> Tứ giác MPQN là hình thang
Do đường thẳng IK đi qua trung điểm cạnh bên MN và song song với hai đáy nên K là trung điểm PQ.
Nên PK = KQ =5dm
Vậy x = 5dm
Kiến thức áp dụng
Đường thẳng đi qua trung điểm của một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm cạnh bên thứ hai.
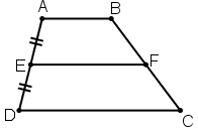
Hình thang ABCD (AB//CD) có: AE = ED, EF//AB// CD
⇒ BF = FC.
Câu 10:
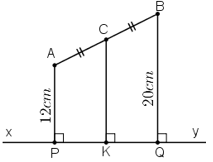
Hai điểm A và B thuộc cùng một nửa mặt phẳng có bờ là đường thẳng xy. Khoảng cách từ điểm A đến xy bằng 12cm, khoảng cách từ điểm B đến xy bằng 20cm. Tính khoảng cách từ trung điểm C của AB đến xy.
 Xem đáp án
Xem đáp án
Gọi P, Q, K lần lượt là chân đường vuông góc hạ từ A, B, C xuống xy.
+ AP ⊥ xy và BQ ⊥ xy ⇒ AP // BQ
⇒ Tứ giác ABQP là hình thang.
+ CK ⊥ xy ⇒ CK // AP//BQ
+ Hình thang ABQP có AC = CB (gt) và CK // AP // BQ
⇒ PK = KQ
⇒ CK là đường trung bình của hình thang
⇒ CK = (AP + BQ)/2.
Mà AP = 12cm, BQ = 20cm ⇒ CK = 16cm.
Vậy khoảng cách từ trung điểm C của AB đến xy bằng 16cm.
Kiến thức áp dụng
Đường thẳng đi qua trung điểm của một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm cạnh bên thứ hai.

Hình thang ABCD (AB//CD) có: AE = ED, EF//AB// CD
⇒ BF = FC.
+ Đường trung bình của hình thang là đoạn thẳng nối trung điểm của hai cạnh bên của hình thang.
+ Đường trung bình của hình thang song song với hai đáy và bằng nửa tổng hai đáy.
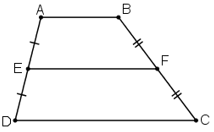
Hình thang ABCD (AB// CD), AE = ED, BF = FC
⇒ EF // AB, EF // CD, EF = (AB + CD)/2.
Câu 11:
Hình thang ABCD có đáy AB, CD. Gọi E, F, K theo thứ tự là trung điểm của AD, BC, BD. Chứng minh ba điểm E, K, F thẳng hàng.
 Xem đáp án
Xem đáp án
+ ΔABD có DE = EA và DK = KB
⇒ EK là đường trung bình của ΔDAB
⇒ EK // AB
+ Hình thang ABCD có: AE = ED và BF = FC
⇒ EF là đường trung bình của hình thang ABCD
⇒ EF // AB// CD
+ Qua điểm E ta có EK // AB và EF // AB nên theo tiên đề Ơclit ta có E, K, F thẳng hàng.
Kiến thức áp dụng
+ Tiên đề Ơ-clit : Qua một điểm nằm ngoài một đường thẳng, ta kẻ được duy nhất một đường thẳng song song với đường thẳng đã cho.
+ Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác
Đường trung bình của tam giác song song với cạnh thứ ba :
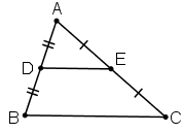
ΔABC, AD = DB, AE = EC ⇒ DE // BC
+ Đường trung bình của hình thang là đoạn thẳng nối trung điểm của hai cạnh bên của hình thang.
Đường trung bình của hình thang song song với hai đáy :
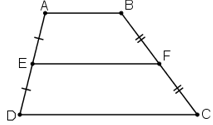
Hình thang ABCD (AB// CD), AE = ED, BF = FC
⇒ EF // AB // CD
Câu 12:
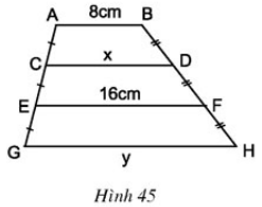
Tính x, y trên hình 45 trong đó AB // CD // EF // GH.
 Xem đáp án
Xem đáp án
+ Tính x :
AB // EF nên tứ giác ABFE là hình thang
Hình thang ABFE có: CA = CE và DB = DF
⇒ CD là đường trung bình của hình thang ABFE
⇒ CD = (AB + EF)/2
hay x = (8 + 16)/2 = 12(cm)
+ Tính y:
CD // GH nên tứ giác CDHG là hình thang
Hình thang CDHG có : EC = EG, FD = FH
⇒ EF là đường trung bình của hình thang CDHG
⇒ EF = (CD + GH)/2
hay (x + y)/2 = 16cm ⇒ x + y = 32cm
Mà x = 12cm ⇒ y = 20cm.
Vậy x = 12cm và y = 20cm.
Kiến thức áp dụng
+ Đường trung bình của hình thang là đoạn thẳng nối trung điểm của hai cạnh bên của hình thang.
Đường trung bình của hình thang bằng nửa tổng hai đáy.

Hình thang ABCD (AB// CD), AE = ED, BF = FC
⇒ EF = (AB + CD)/2.
Câu 13:
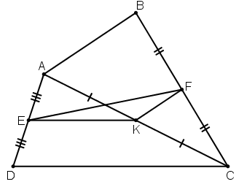
Cho tứ giác ABCD. Gọi E, F, K theo thứ tự là trung điểm của AD, BC, AC.
a) So sánh các độ dài EK và CD, KF và AB
b) Chứng minh rằng
 Xem đáp án
Xem đáp án
a) + ΔADC có: AE = ED (gt) và AK = KC (gt)
⇒ EK là đường trung bình của ΔADC
⇒ EK = CD/2
+ ΔABC có AK = KC (gt) và BF = FC (gt)
⇒ KF là đường trung bình của ΔABC
⇒ KF = AB/2.
b) Ta có: EF ≤ EK + KF =
(Bổ sung: 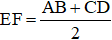
Kiến thức áp dụng
+ Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác
Đường trung bình của tam giác bằng một nửa cạnh còn lại :

ΔABC, AD = DB, AE = EC ⇒ DE = BC/2.
Câu 14:
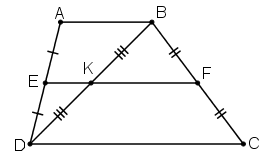
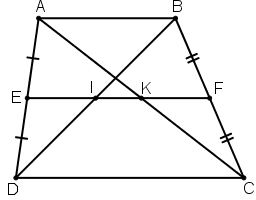
Cho hình thang ABCD (AB // CD), E là trung điểm của AD, F là trung điểm của BC. Đường thẳng EF cắt BD tại I, cắt AC ở K.
a) Chứng minh rằng AK = KC, BI = ID.
b) Cho AB = 6cm, CD = 10cm. Tính các độ dài EI, KF, IK.
 Xem đáp án
Xem đáp án
a) + Hình thang ABCD có EA = ED, FB = FC (gt)
⇒ EF là đường trung bình của hình thang ABCD.
⇒ EF // AB // CD
+ ΔABC có BF = FC (gt) và FK // AB (cmt)
⇒ AK = KC
+ ΔABD có: AE = ED (gt) và EI // AB (cmt)
⇒ BI = ID
b) + Vì EF là đường trung bình của hình thang ABCD.
⇒ EF = (AB + CD)/2 = (6 + 10)/2 = 8cm.
+ ΔABD có AE = ED, DI = IB
⇒ EI là đường trung bình của ΔABD
⇒ EI = AB/2 = 6/2 = 3(cm)
+ ΔABC có CF = BF, CK = AK
⇒ KF là đường trung bình của ΔABC
⇒ KF = AB /2 = 6/2 = 3cm
+ Lại có: EI + IK + KF = EF
⇒ IK = EF – EI – KF = 8 – 3 – 3 = 2cm
Kiến thức áp dụng
+ Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba:
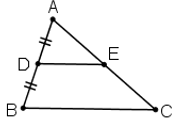
ΔABC, AD = DB , DE // BC ⇒ AE = EC.
+ Đường trung bình của tam giác song song với cạnh thứ ba và bằng một nửa cạnh đó.

ΔABC, AD = DB, AE = EC ⇒ DE // BC và DE = BC/2.
+ Đường trung bình của hình thang là đoạn thẳng nối trung điểm của hai cạnh bên. Đường trung bình của hình thang song song với hai đáy và bằng nửa tổng hai đáy.

Hình thang ABCD (AB// CD), AE = ED, BF = FC
⇒ EF // AB // CD, EF = (AB + CD)/2.