Bài tập chuyên đề Toán 6 Hình thoi có đáp án
-
398 lượt thi
-
21 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Xem đáp án
Lời giải
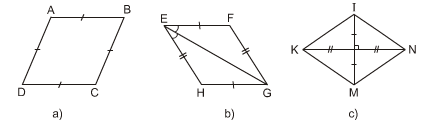
Các tứ giác ở hình 102a, b, c, e là hình thoi.
- Hình 102a: \[ABCD\] là hình thoi (theo dấu hiệu nhận biết số 1)
- Hình 102b: \[{\rm{EFGH}}\] là hình thoi (theo dấu hiệu nhận biết 4)
- Hình 102c: \[{\rm{KINM}}\] là hình thoi (theo dấu hiệu nhận biết 3)
Câu 2:
Xem đáp án
Lời giải
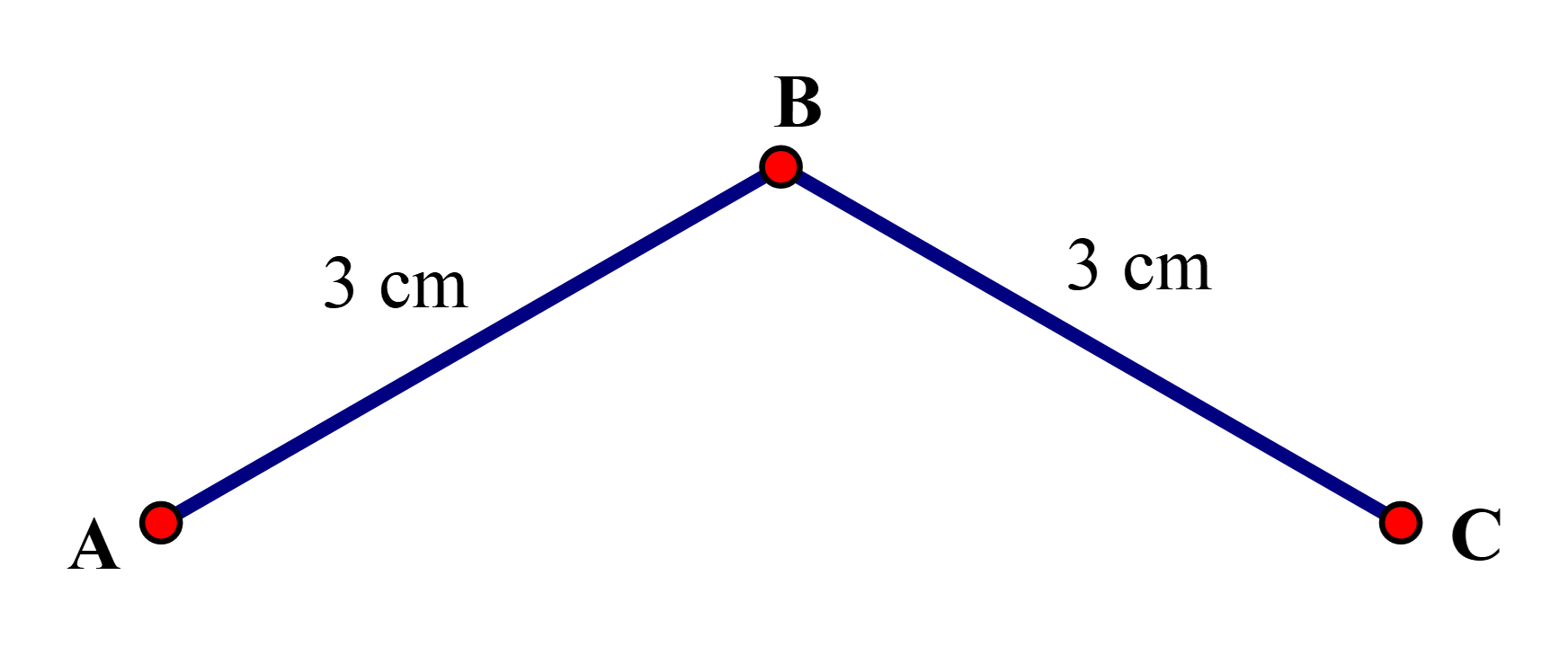
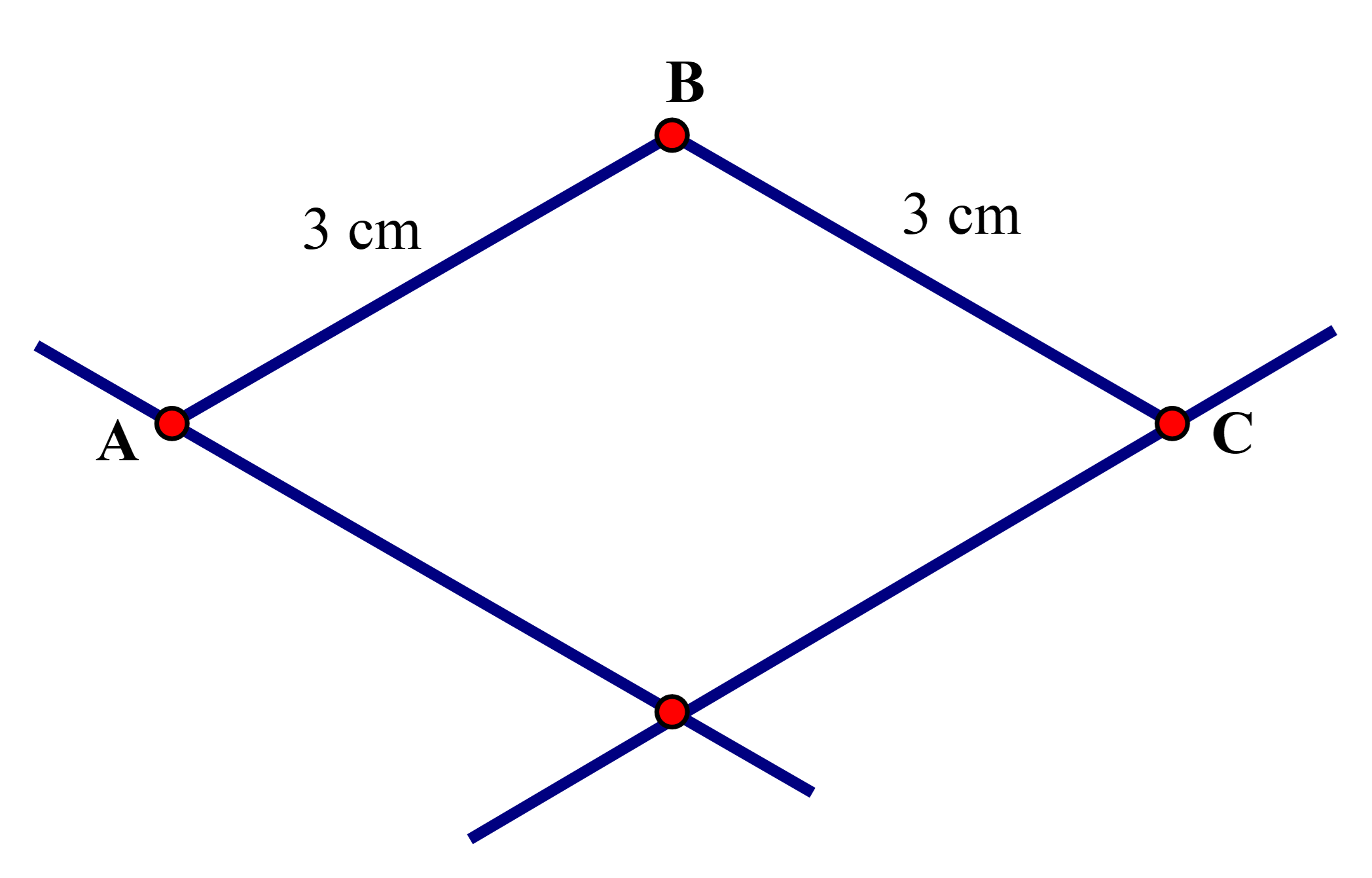
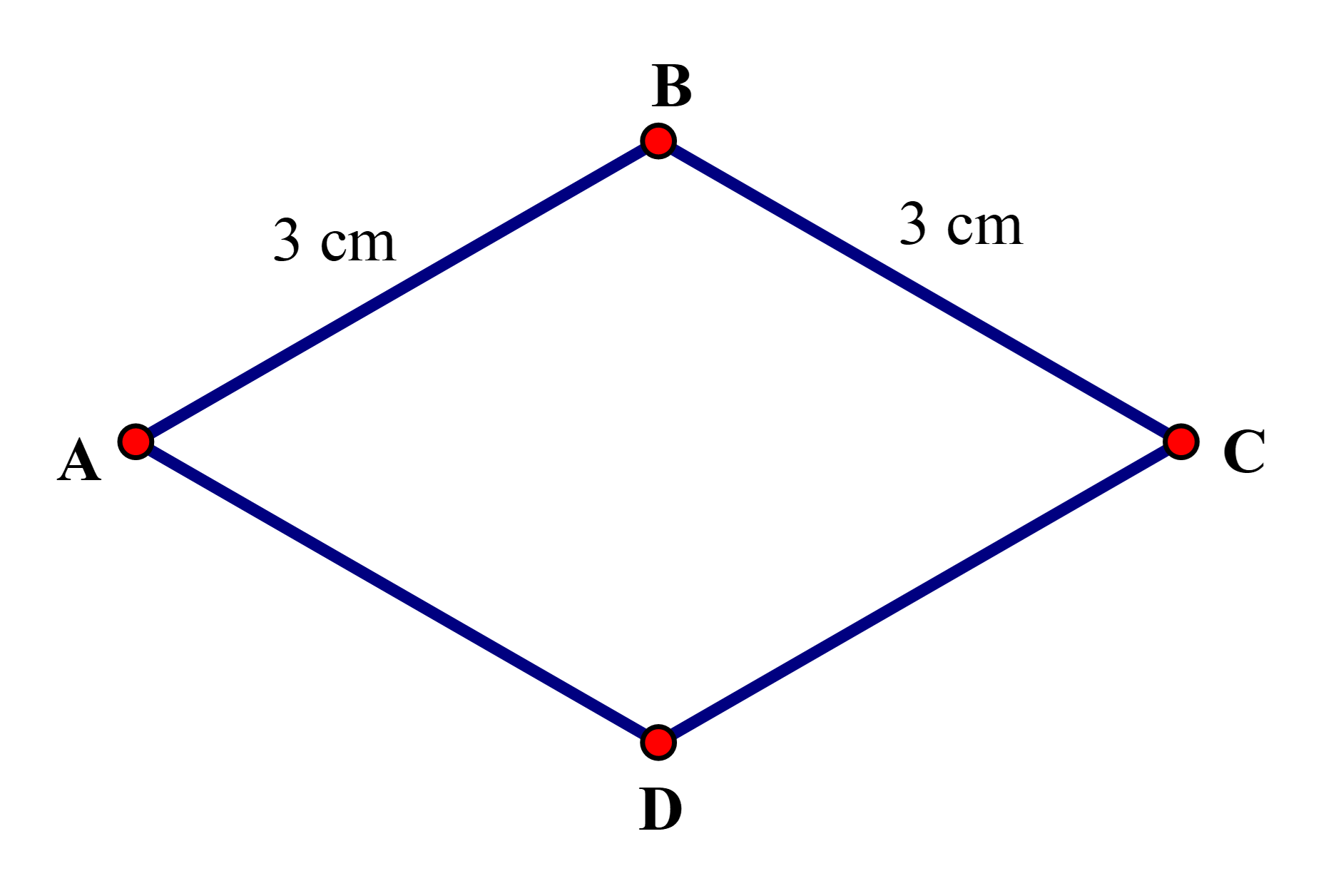
Câu 3:
Xem đáp án
Lời giải
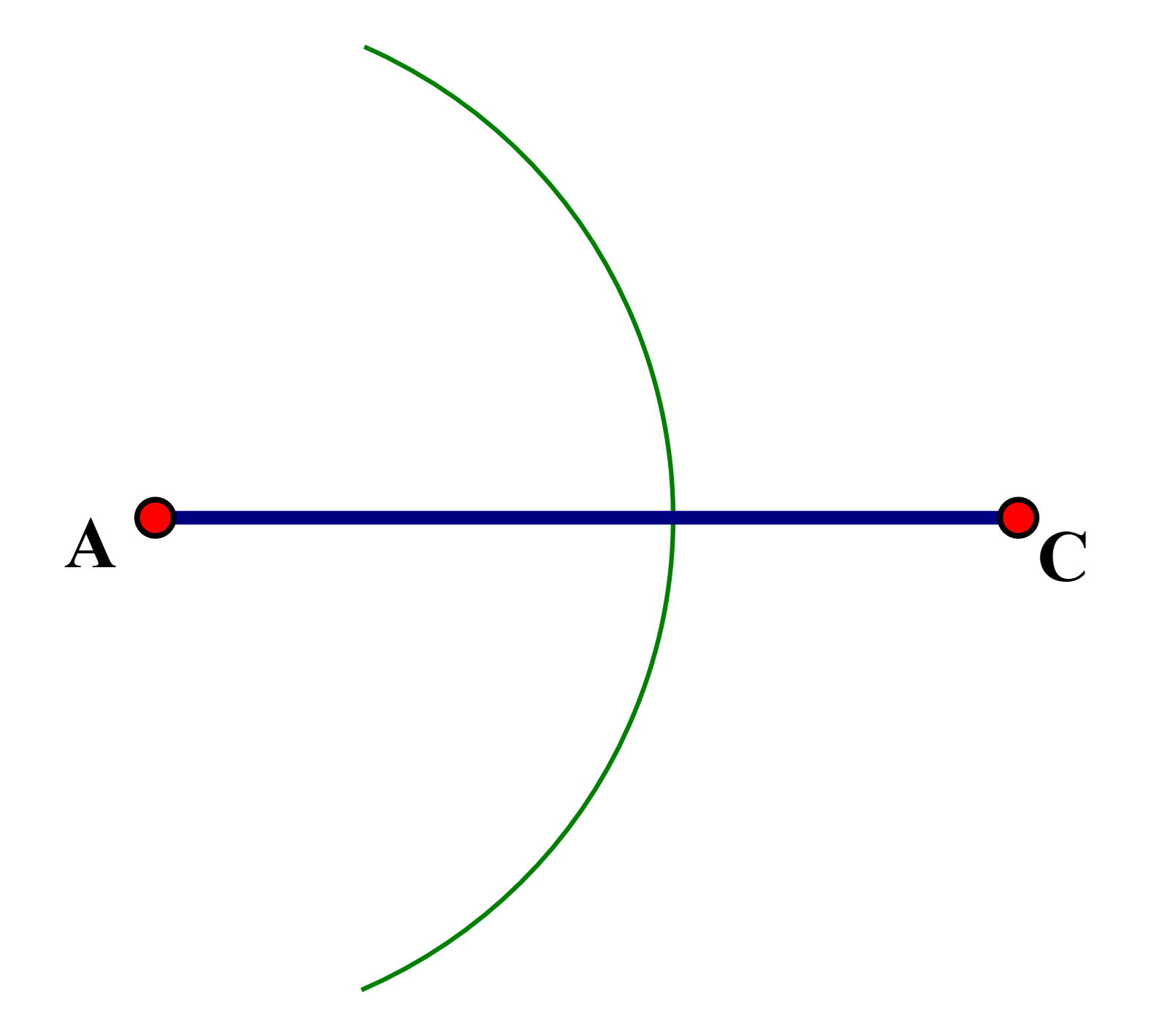
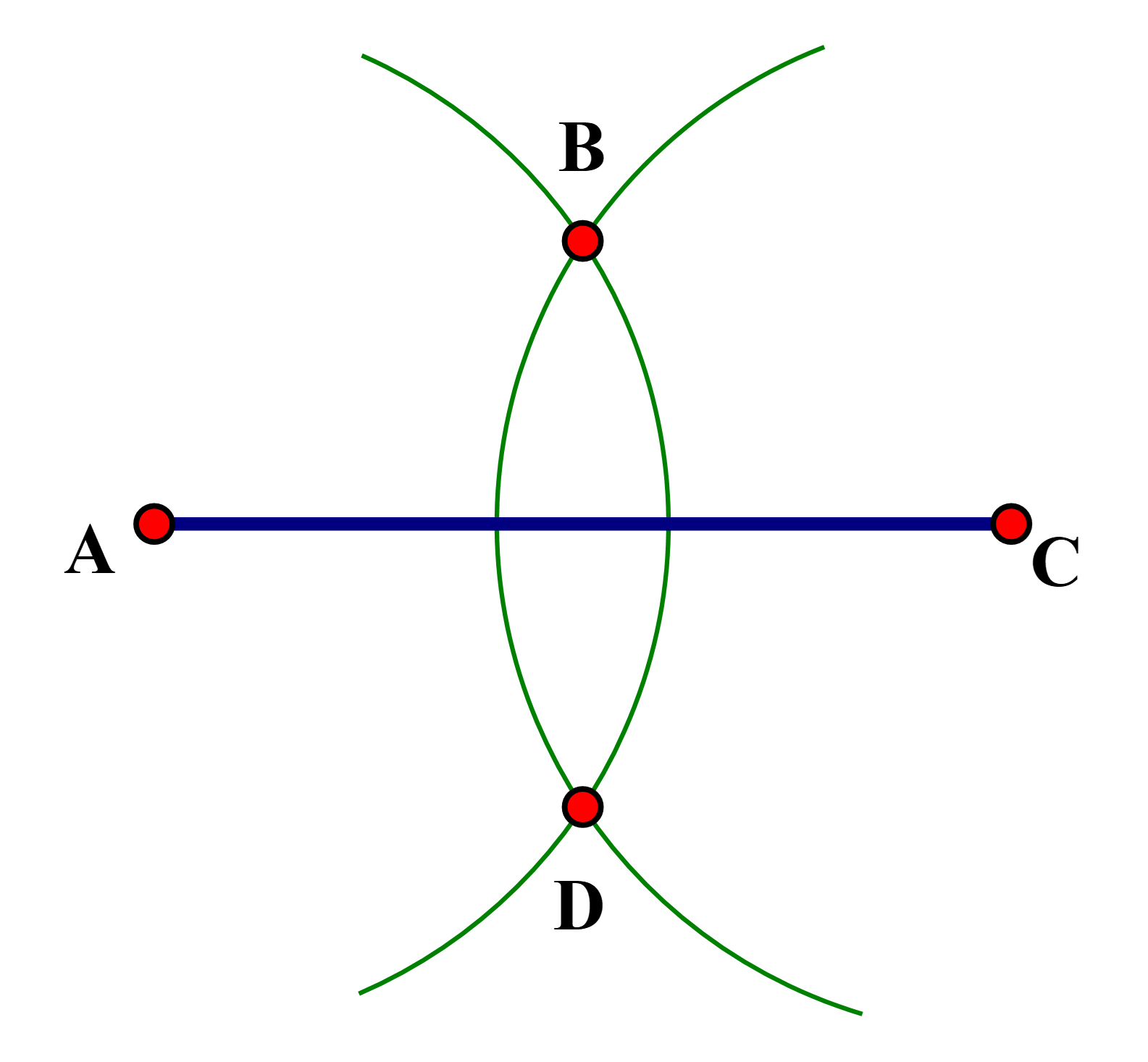
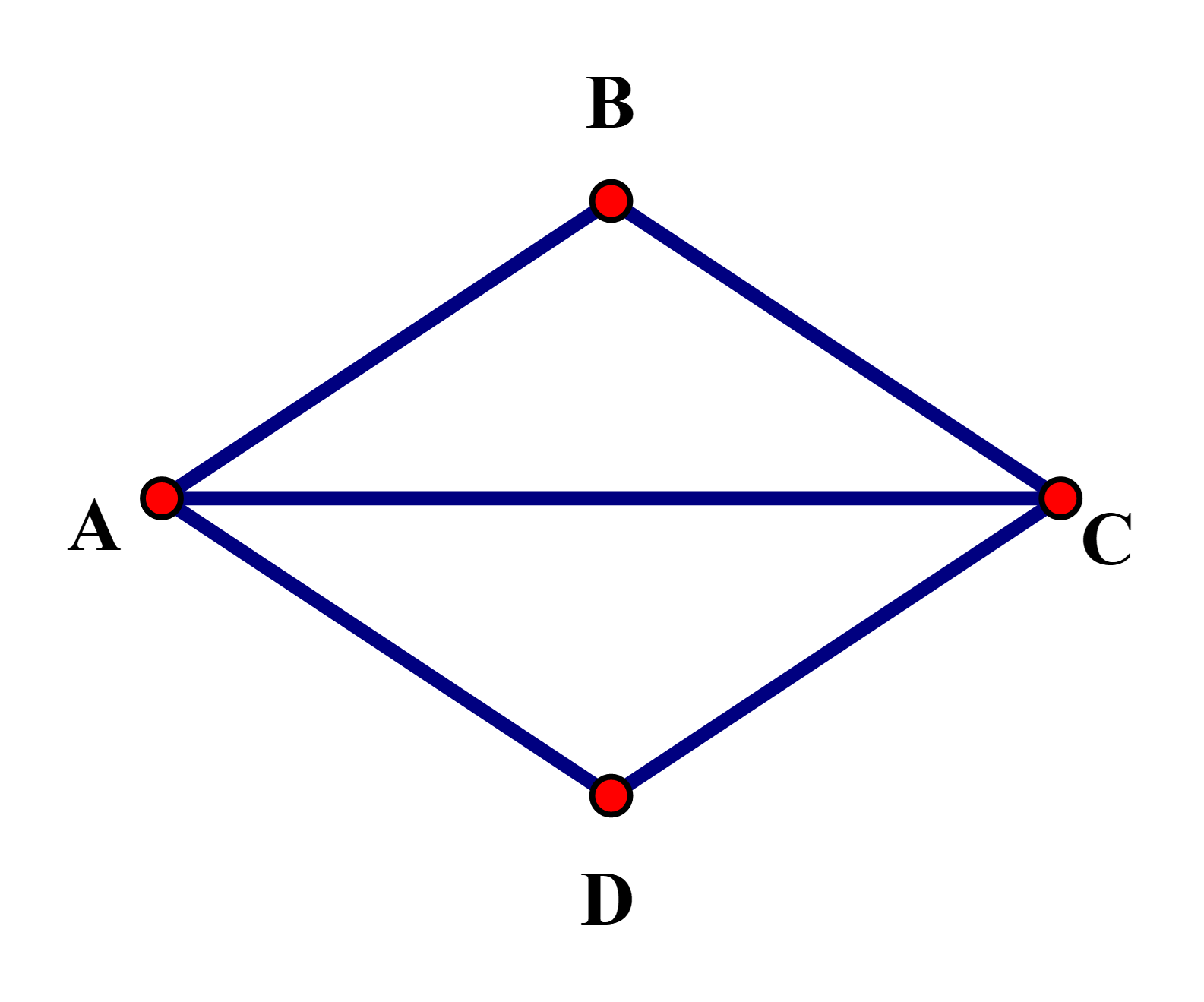
Câu 5:
Xem đáp án
Lời giải
Cách vẽ tương tự bài 2
Câu 6:
Tính diện tích hình thoi, biết:
Độ dài các đường chéo là \[30{\rm{ }}cm\] và \[7{\rm{ }}cm\].
Xem đáp án
Lời giải
Diện tích của hình thoi là: \[30.72 = 105(c{m^2})\].
Câu 7:
Tính diện tích hình thoi, biết:
Xem đáp án
Lời giải
Đổi 4m = 40dm.
Diện tích của hình thoi là: \[40.152 = 300(d{m^2})\].
Câu 8:
Tính diện tích hình thoi \[MBND\]biết \[ABCD\] là hình vuông và hai đường chéo của hình vuông \[AC = BD = 20{\rm{ c}}m\]( \[M\]là điểm chính giữa AO; N là điểm chính giữa OC)
Xem đáp án
Lời giải
Hai đường chéo hình vuông bằng nhau và cắt nhau tại trung điểm mỗi đường nên
\[OA = OC = 20:2 = 10(cm)\]
Vì điểm M, N là các điểm chính giữa của OA, OC nên:
\[OM = ON = OA:2 = 10:2 = 5(cm)\]
Do đó hình thoi \[MBND\] có độ dài đường chéo \[MN = 2.OM = 2.5 = 10(cm)\]
Đường chéo \[BD = 20(cm)\]
Diện tích hình thoi \[MBND\] là \[\frac{1}{2}MN.BD = \frac{1}{2}10.20 = 100(c{m^2})\]
Câu 9:
Xem đáp án
Lời giải
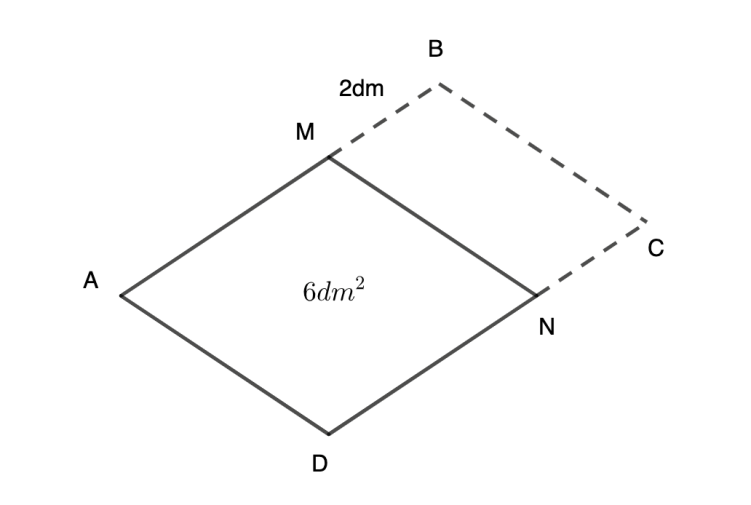
\[AMND\] là hình thoi nên \[AM = MN = DN = AD\]
\[ABCD\]là hình bình hành nên \[BC = AD\]
\[ \Rightarrow AM = BC = DN = AD\]
Chu vi hình bình hành là:
\[AM + BC + DN + AD + MB + NC = 4DN + 2MB = 2m = 20dm\]
\[ \Rightarrow 4DN + 2.2 = 20 \Rightarrow {\rm{4DN = 16}} \Rightarrow {\rm{DN = 4(dm)}}\]
Gọi h là độ dài đường cao của hình thoi AMND kẻ từ điểm M xuống cạnh DN
\[h = {S_{AMND}}:DN = 6:4 = 1,5(dm)\]
h đồng thời là độ dài đường cao của hình bình hành ABCD
Diện tích hình bình hành là: \[{S_{ABCD}} = CD.h = \left( {4 + 2} \right).1,5 = 9(d{m^2})\]
Câu 10:
Một mảnh vườn hình thoi có tổng độ dài hai đường chéo là \[220{\rm{ m}}\], biết đường chéo thứ nhất bằng \[\frac{2}{3}\]độ dài đường chéo thứ hai
Tính diện tích mảnh vườn đó.
Xem đáp án
Lời giải
Độ dài đường chéo lớn là \[220:\left( {2 + 3} \right).3 = 132{\rm{ }}\left( m \right)\]
Độ dài đường chéo nhỏ là \[220 - 132{\rm{ = 88}}\left( m \right)\]
Diện tích mảnh vườn là \[\frac{1}{2} \cdot 132 \cdot 88 = 5808\left( {{m^2}} \right)\]
Câu 11:
Người ta dành \[\frac{1}{{16}}\]diện tích mảnh vườn để làm nhà ở và vườn hoa. Tính diện tích để làm nhà ở và vườn hoa.
Xem đáp án
Lời giải
Diện tích để làm nhà ở và vườn hoa là\[\frac{1}{{16}} \cdot 5808 = 363\left( {{m^2}} \right)\]
Câu 12:
Một mảnh vườn hình thoi có tổng hai đường chéo bằng \[71{\rm{ m}}\], đường chéo thứ nhất hơn đường chéo thứ hai \[10{\rm{ m}}\].
Tìm độ dài mỗi đường chéo.
Xem đáp án
Lời giải
Đường chéo thứ hai của mảnh vườn là \[\left( {71 - 10} \right):2 = 30,5\left( m \right)\]
Đường chéo thứ nhất của mảnh vườn là \[71 - 30,5 = 40,5\left( m \right)\]
Câu 13:
Tính diện tích mảnh vườn.
Xem đáp án
Lời giải
Câu 14:
Xem đáp án
Lời giải
Số phần trăm diện tích còn lại của mảnh vườn là \[100 - \left( {25 + 46,5} \right) = 28,5\% \]
Câu 15:
Xem đáp án
Lời giải
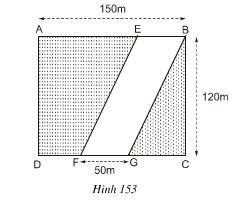
Con đường hình bình hành EBGF có diện tích: \[{S_{EBGF}} = 50.120 = 6000{m^2}\]
Đám đất hình chữ nhật ABCD có diện tích: \[{S_{ABCD}} = 150.120 = 18000{m^2}\]
Diện tích phần còn lại của đám đất: \[S = {S_{ABCD}} - {S_{EBGF}} = 18000 - 6000 = 12000{m^2}\]
Câu 16:
Xem đáp án
Hướng dẫn giải
Độ dài đường chéo bé là \(\left( {17 - 3} \right):2 = 7\left( m \right)\).
Độ dài đường chéo lớn là \(7 + 3 = 10\left( m \right)\).
Diện tích vườn hoa hình thoi là \(\frac{1}{2} \cdot 7 \cdot 10 = 35\left( {{m^2}} \right)\).
Câu 17:
Xem đáp án
Hướng dẫn giải
Độ dài đường chéo bé là \(\left( {56 - 16} \right):2 = 20\left( m \right)\).
Độ dài đường chéo lớn là \(20 + 16 = 36\left( m \right)\).
Diện tích thửa ruộng hình thoi là \(\frac{1}{2} \cdot 20 \cdot 36 = 360\left( {{m^2}} \right)\).
Câu 18:
Xem đáp án
Hướng dẫn giải
Vì đường chéo thứ nhất bằng một nửa đường chéo thứ hai hay đường chéo thứ hai gấp đôi đường chéo thứ nhất.
Tổng số phần bằng nhau là \(2 + 1 = 3\) (phần).
Độ dài đường chéo thứ nhất là \(120:3.1 = 40\left( {cm} \right)\).
Độ dài đường chéo thứ hai là \(120:3.2 = 80\left( {cm} \right)\).
Diện tích mảnh vườn hình thoi là \(\frac{1}{2} \cdot 40 \cdot 80 = 1600\left( {c{m^2}} \right)\)
Câu 19:
Xem đáp án
Hướng dẫn giải
Độ dài đường chéo thứ hai là \(175.\frac{4}{7} = 100\left( m \right)\).
Diện tích mảnh đất hình thoi là \(\frac{1}{2} \cdot 175 \cdot 100 = 8750\left( {{m^2}} \right)\).
Diện tích trồng hoa là \(\frac{1}{2} \cdot 8750 = 4375\left( {{m^2}} \right)\).
Câu 20:
Xem đáp án
Hướng dẫn giải
Cạnh của hình vuông là \(200:4 = 50\left( m \right)\).
Đường chéo thứ nhất có độ dài bằng cạnh của hình vuông nên bằng \(50\,m\).
Độ dài đường chéo thứ hai là \(120 - 50 = 70\,m\).
Diện tích hình thoi là \(\frac{1}{2} \cdot 70.50 = 1750\left( {{m^2}} \right)\).
Câu 21:
Xem đáp án
Hướng dẫn giải
Diện tích mảnh vườn hình thoi là \(\frac{1}{2} \cdot 9 \cdot 6 = 27\left( {{m^2}} \right)\).
Diện tích bể cá hình tròn là \({3,14.1,5^2} = 7,065\left( {{m^2}} \right)\).
Diện tích phần vườn trồng hoa là \(27 - 7,065 = 19,935\left( {{m^2}} \right)\).