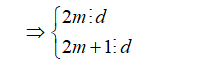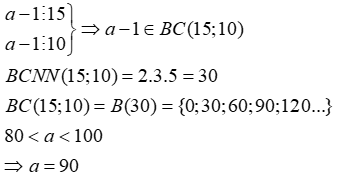Cách tìm ước chung lớn nhất, bội chung nhỏ nhất cực hay có đáp án
-
531 lượt thi
-
15 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 3:
Biết số học sinh của một trường trong khoảng từ 400 đến 500 học sinh. Khi tập thể dục giữa giờ thì xếp thành các hàng có số học sinh bằng nhau thì thấy xếp thành 12 hàng, 15 hàng, 21 hàng đều vừa đủ. Tính số học sinh của trường đó.
Xem đáp án
12=22.3 ; 15=3.5; 21=3.7
BCNN (12;15;21) = .3.5.7=420
BC( 12; 15;21) chính là bội của BCNN(12;15;21)
⇒ BC(12;15;21)= B(420) = {0,420,840,.....}
Số học sinh 400 ≤ x ≤ 450
⇒ Số học sinh là 420 học sinh.
Câu 4:
Tìm 2 số tự nhiên a và b. Biết a > b và tổng của 2 số bằng 500 và UCLN (a;b)=100
Xem đáp án
UCLN(a;b)=100
a=100m; b=100n
(m;n)=1 và m > n
a+b = 100m +100n =500
100(m+n) =500
m+n =5
m=3 và n=2 → a=300;b=200
M=4 và n=1 → a=400;b=100
Câu 5:
Cho m ∈ N* chứng minh rằng hai số có dạng 2m và 2m+1 nguyên tố cùng nhau
Xem đáp án
Gọi ƯCLN (2m;2m+1)=d
(2m+1) -2m ⋮ d → 1 ⋮ d → d=1
ƯCLN(2m,2m+1) =1
Vậy 2m và 2m+1 là số nguyên tố cùng nhau
Câu 8:
Tìm ƯC(12; 30)?
Xem đáp án
Đáp án: C
Ta có: 12 = 22.3
30 = 2.3.5
ƯCLN(12; 30) = 2.3 = 6
ƯC(12; 30) = U(6) = {1; 2; 3; 6}
Câu 9:
Tìm số tự nhiên a biết rằng a chia 15 dư 1 và a chia 10 dư 1, và 80 < a < 100
Xem đáp án
Đáp án: A
Câu 10:
Tìm ƯCLN (48; 168; 360)
Xem đáp án
Đáp án: A
Tìm ƯCLN (48; 168; 360)
48 = 24.3
168 = 23.3.7
360 = 23.32.5
ƯCLN (48; 168; 360) = 23.3 = 24
A. 24
B. 45
C. 168
D. 40
Câu 11:
Tìm BCNN (9; 10; 11)
Xem đáp án
Đáp án: D
Tìm BCNN (9; 10; 11)
9 =
10 = 2.5
11 = 11
BCNN (9; 10; 11) = 2. .5.11 = 990
Câu 12:
Tìm bội chung của 15 và 25 mà nhỏ hơn 400
Xem đáp án
Đáp án: A
A. 0, 75, 150, 225, 300, 375 → Đúng vì BCNN(15,25) = 75 BC(15,25) = B(75)
B. 0, 75, 150, 225, 300 → Sai vì thiếu 375
C. 75, 150, 225, 300, 375 → Sai vì thiếu số 0
D. 0, 75, 225, 300, 375 → Sai vì thiếu 150
Câu 13:
Chọn khẳng định sai:
Xem đáp án
Đáp án: D
A. Để tìm bội chung của các số đã cho, ta có thể tìm các bội của BCNN của các số đó → Đúng
B. Bội chung nhỏ nhất của hai hay nhiều số là số nhỏ nhất khác 0 trong tập hợp các bội chung của các số đó → Đúng
C. Mọi số tự nhiên đều là bội của 1 → Đúng
D. Nếu a chia hết cho m, a chia hết cho n thì a không chia hết cho BCNN của m và n → Sai
Câu 14:
Một số sách khi xếp thành từng bó 10 cuốn, 12 cuốn, 15 cuốn, 18 cuốn đề vừa đủ bó. Biết số sách trong khoảng từ 200 đến 500. Tính số sách.
Xem đáp án
Đáp án: C
Gọi x là số sách 200< x < 500 x là số nguyên
Ta có:
Câu 15:
Tìm các bội chung có ba chữ số của 63, 35 và 105
Xem đáp án
Đáp án: A
63 = . 7
35 = 5.7
105 = 3.5.7
BCNN(63,35,105) = 32.5.7 = 315
BC(63, 35 , 105) = B(315) = {0;315;630;945;1260;…}
Vì số cần tìm có 3 chữ số
Vậy đó là các số 315;630;945